On the phase diagram of extensive-rank symmetric matrix denoising beyond rotational invariance

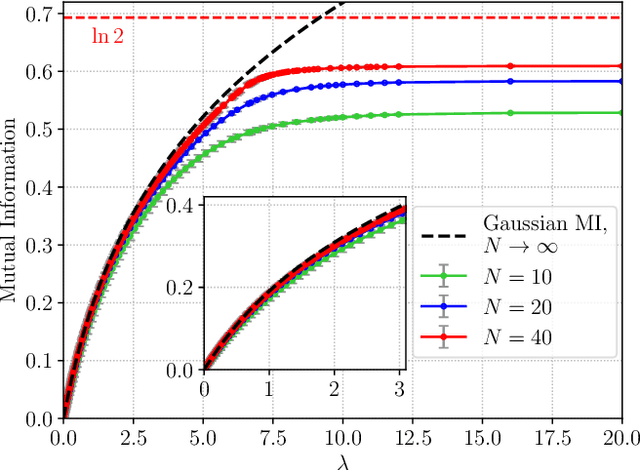
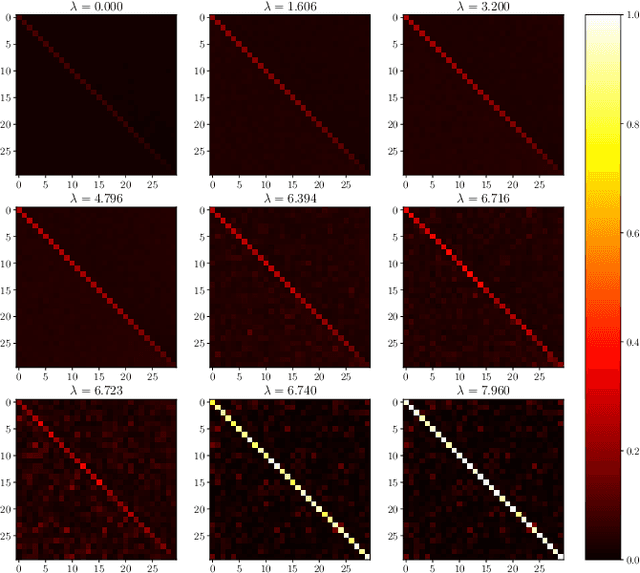
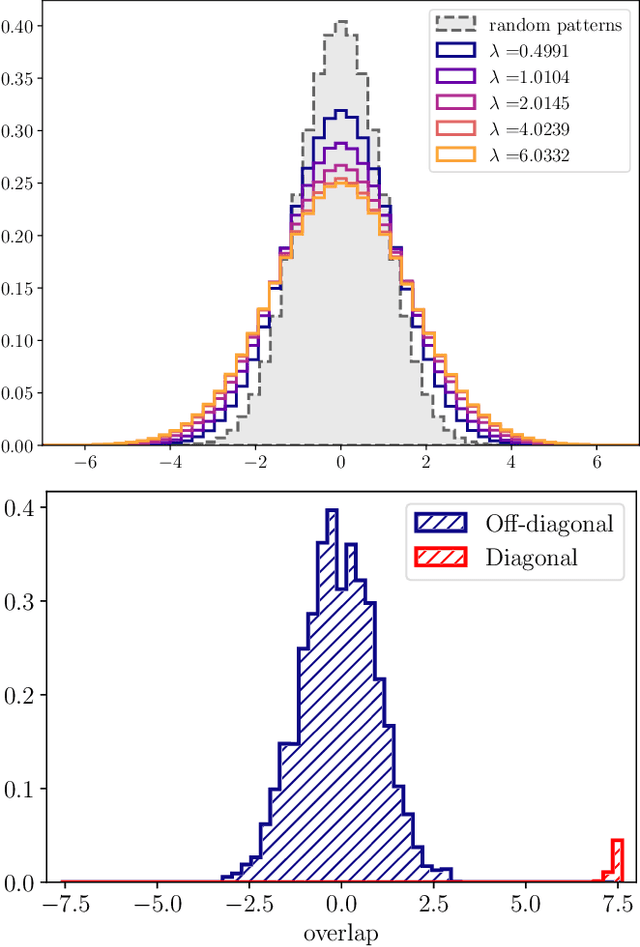
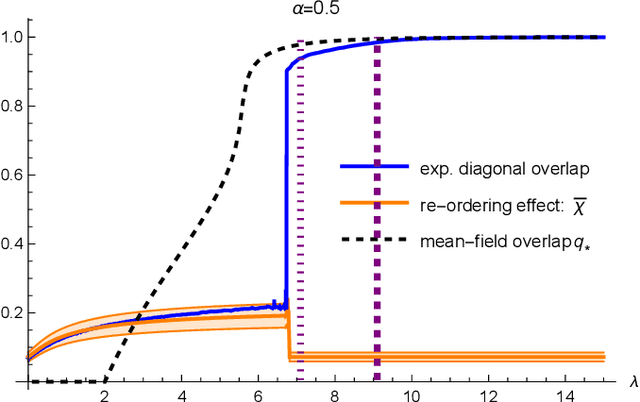
Matrix denoising is central to signal processing and machine learning. Its analysis when the matrix to infer has a factorised structure with a rank growing proportionally to its dimension remains a challenge, except when it is rotationally invariant. In this case the information theoretic limits and a Bayes-optimal denoising algorithm, called rotational invariant estimator [1,2], are known. Beyond this setting few results can be found. The reason is that the model is not a usual spin system because of the growing rank dimension, nor a matrix model due to the lack of rotation symmetry, but rather a hybrid between the two. In this paper we make progress towards the understanding of Bayesian matrix denoising when the hidden signal is a factored matrix $XX^\intercal$ that is not rotationally invariant. Monte Carlo simulations suggest the existence of a denoising-factorisation transition separating a phase where denoising using the rotational invariant estimator remains Bayes-optimal due to universality properties of the same nature as in random matrix theory, from one where universality breaks down and better denoising is possible by exploiting the signal's prior and factorised structure, though algorithmically hard. We also argue that it is only beyond the transition that factorisation, i.e., estimating $X$ itself, becomes possible up to sign and permutation ambiguities. On the theoretical side, we combine mean-field techniques in an interpretable multiscale fashion in order to access the minimum mean-square error and mutual information. Interestingly, our alternative method yields equations which can be reproduced using the replica approach of [3]. Using numerical insights, we then delimit the portion of the phase diagram where this mean-field theory is reliable, and correct it using universality when it is not. Our ansatz matches well the numerics when accounting for finite size effects.

Information limits and Thouless-Anderson-Palmer equations for spiked matrix models with structured noise

We consider a prototypical problem of Bayesian inference for a structured spiked model: a low-rank signal is corrupted by additive noise. While both information-theoretic and algorithmic limits are well understood when the noise is i.i.d. Gaussian, the more realistic case of structured noise still proves to be challenging. To capture the structure while maintaining mathematical tractability, a line of work has focused on rotationally invariant noise. However, existing studies either provide sub-optimal algorithms or they are limited to a special class of noise ensembles. In this paper, we establish the first characterization of the information-theoretic limits for a noise matrix drawn from a general trace ensemble. These limits are then achieved by an efficient algorithm inspired by the theory of adaptive Thouless-Anderson-Palmer (TAP) equations. Our approach leverages tools from statistical physics (replica method) and random matrix theory (generalized spherical integrals), and it unveils the equivalence between the rotationally invariant model and a surrogate Gaussian model.

The Decimation Scheme for Symmetric Matrix Factorization

Matrix factorization is an inference problem that has acquired importance due to its vast range of applications that go from dictionary learning to recommendation systems and machine learning with deep networks. The study of its fundamental statistical limits represents a true challenge, and despite a decade-long history of efforts in the community, there is still no closed formula able to describe its optimal performances in the case where the rank of the matrix scales linearly with its size. In the present paper, we study this extensive rank problem, extending the alternative 'decimation' procedure that we recently introduced, and carry out a thorough study of its performance. Decimation aims at recovering one column/line of the factors at a time, by mapping the problem into a sequence of neural network models of associative memory at a tunable temperature. Though being sub-optimal, decimation has the advantage of being theoretically analyzable. We extend its scope and analysis to two families of matrices. For a large class of compactly supported priors, we show that the replica symmetric free entropy of the neural network models takes a universal form in the low temperature limit. For sparse Ising prior, we show that the storage capacity of the neural network models diverges as sparsity in the patterns increases, and we introduce a simple algorithm based on a ground state search that implements decimation and performs matrix factorization, with no need of an informative initialization.

Fundamental limits of overparametrized shallow neural networks for supervised learning

We carry out an information-theoretical analysis of a two-layer neural network trained from input-output pairs generated by a teacher network with matching architecture, in overparametrized regimes. Our results come in the form of bounds relating i) the mutual information between training data and network weights, or ii) the Bayes-optimal generalization error, to the same quantities but for a simpler (generalized) linear model for which explicit expressions are rigorously known. Our bounds, which are expressed in terms of the number of training samples, input dimension and number of hidden units, thus yield fundamental performance limits for any neural network (and actually any learning procedure) trained from limited data generated according to our two-layer teacher neural network model. The proof relies on rigorous tools from spin glasses and is guided by ``Gaussian equivalence principles'' lying at the core of numerous recent analyses of neural networks. With respect to the existing literature, which is either non-rigorous or restricted to the case of the learning of the readout weights only, our results are information-theoretic (i.e. are not specific to any learning algorithm) and, importantly, cover a setting where all the network parameters are trained.

Matrix factorization with neural networks

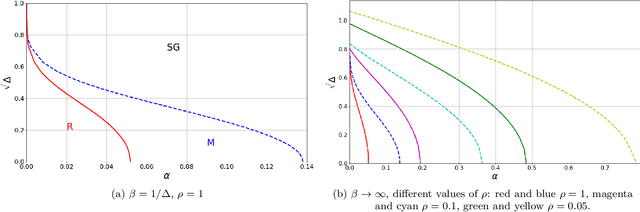
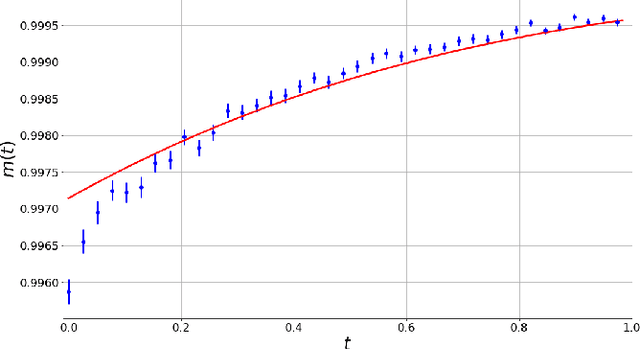
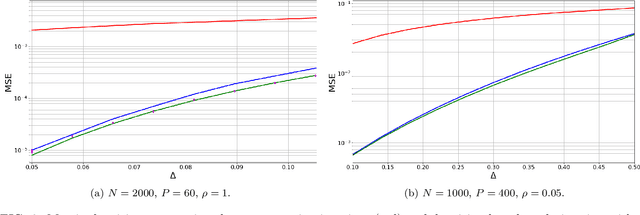
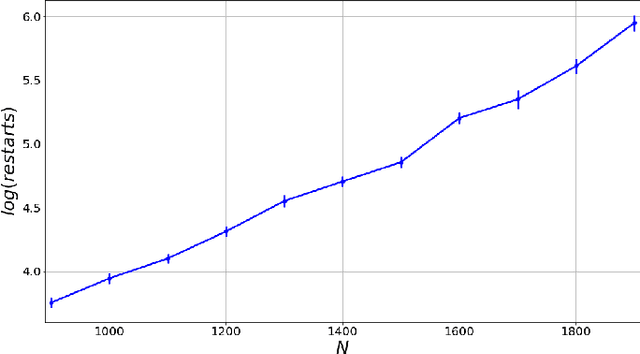
Matrix factorization is an important mathematical problem encountered in the context of dictionary learning, recommendation systems and machine learning. We introduce a new `decimation' scheme that maps it to neural network models of associative memory and provide a detailed theoretical analysis of its performance, showing that decimation is able to factorize extensive-rank matrices and to denoise them efficiently. We introduce a decimation algorithm based on ground-state search of the neural network, which shows performances that match the theoretical prediction.

Bayes-optimal limits in structured PCA, and how to reach them

We study the paradigmatic spiked matrix model of principal components analysis, where the rank-one signal is corrupted by additive noise. While the noise is typically taken from a Wigner matrix with independent entries, here the potential acting on the eigenvalues has a quadratic plus a quartic component. The quartic term induces strong correlations between the matrix elements, which makes the setting relevant for applications but analytically challenging. Our work provides the first characterization of the Bayes-optimal limits for inference in this model with structured noise. If the signal prior is rotational-invariant, then we show that a spectral estimator is optimal. In contrast, for more general priors, the existing approximate message passing algorithm (AMP) falls short of achieving the information-theoretic limits, and we provide a justification for this sub-optimality. Finally, by generalizing the theory of Thouless-Anderson-Palmer equations, we cure the issue by proposing a novel AMP which matches the theoretical limits. Our information-theoretic analysis is based on the replica method, a powerful heuristic from statistical mechanics; instead, the novel AMP comes with a rigorous state evolution analysis tracking its performance in the high-dimensional limit. Even if we focus on a specific noise distribution, our methodology can be generalized to a wide class of trace ensembles, at the cost of more involved expressions.