Statistical mechanics of extensive-width Bayesian neural networks near interpolation

For three decades statistical mechanics has been providing a framework to analyse neural networks. However, the theoretically tractable models, e.g., perceptrons, random features models and kernel machines, or multi-index models and committee machines with few neurons, remained simple compared to those used in applications. In this paper we help reducing the gap between practical networks and their theoretical understanding through a statistical physics analysis of the supervised learning of a two-layer fully connected network with generic weight distribution and activation function, whose hidden layer is large but remains proportional to the inputs dimension. This makes it more realistic than infinitely wide networks where no feature learning occurs, but also more expressive than narrow ones or with fixed inner weights. We focus on the Bayes-optimal learning in the teacher-student scenario, i.e., with a dataset generated by another network with the same architecture. We operate around interpolation, where the number of trainable parameters and of data are comparable and feature learning emerges. Our analysis uncovers a rich phenomenology with various learning transitions as the number of data increases. In particular, the more strongly the features (i.e., hidden neurons of the target) contribute to the observed responses, the less data is needed to learn them. Moreover, when the data is scarce, the model only learns non-linear combinations of the teacher weights, rather than "specialising" by aligning its weights with the teacher's. Specialisation occurs only when enough data becomes available, but it can be hard to find for practical training algorithms, possibly due to statistical-to-computational~gaps.

Optimal generalisation and learning transition in extensive-width shallow neural networks near interpolation

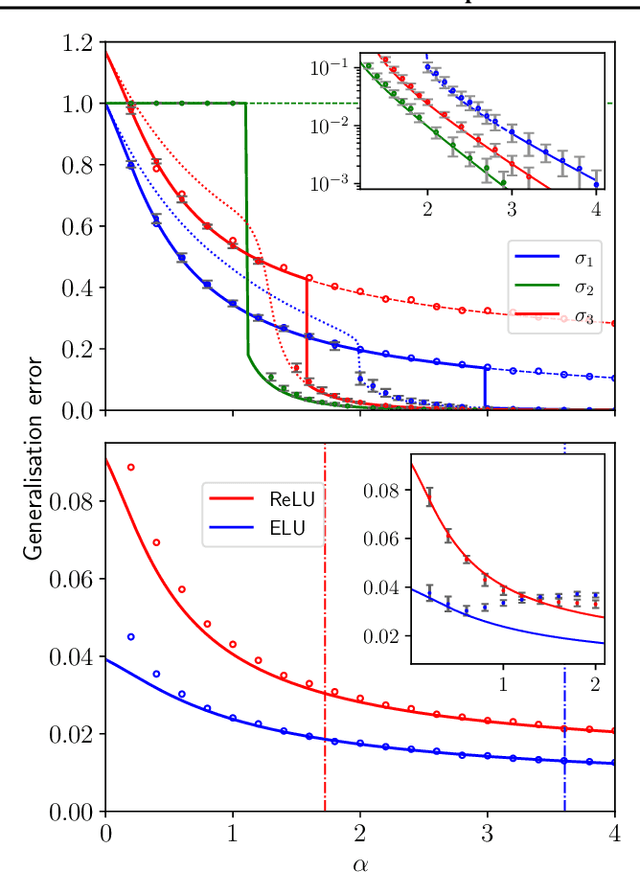
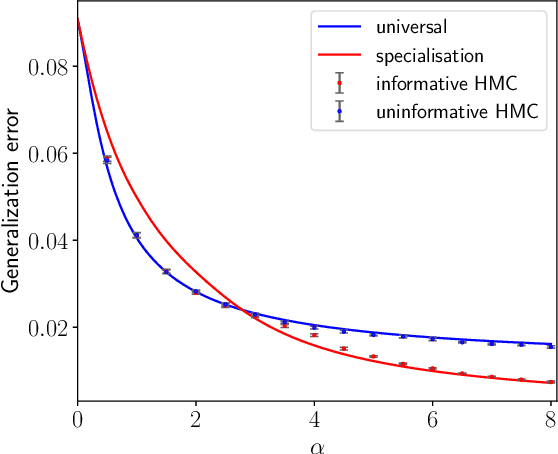
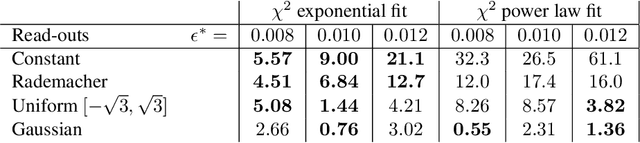
We consider a teacher-student model of supervised learning with a fully-trained 2-layer neural network whose width $k$ and input dimension $d$ are large and proportional. We compute the Bayes-optimal generalisation error of the network for any activation function in the regime where the number of training data $n$ scales quadratically with the input dimension, i.e., around the interpolation threshold where the number of trainable parameters $kd+k$ and of data points $n$ are comparable. Our analysis tackles generic weight distributions. Focusing on binary weights, we uncover a discontinuous phase transition separating a "universal" phase from a "specialisation" phase. In the first, the generalisation error is independent of the weight distribution and decays slowly with the sampling rate $n/d^2$, with the student learning only some non-linear combinations of the teacher weights. In the latter, the error is weight distribution-dependent and decays faster due to the alignment of the student towards the teacher network. We thus unveil the existence of a highly predictive solution near interpolation, which is however potentially hard to find.

Asymptotic Bayes risk of semi-supervised multitask learning on Gaussian mixture

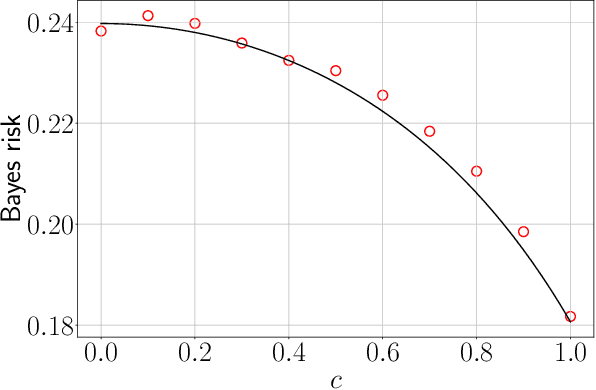
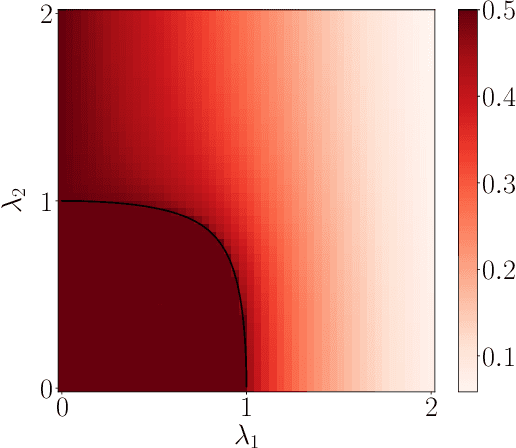
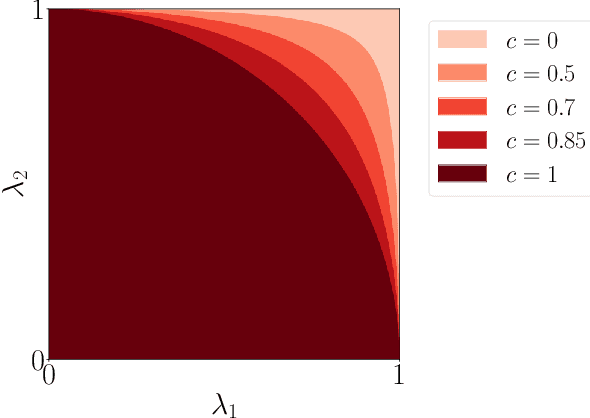
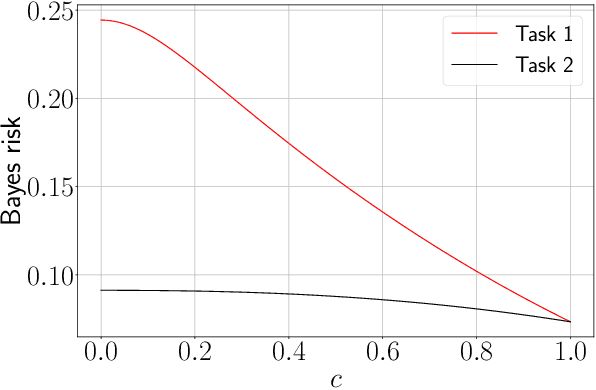
The article considers semi-supervised multitask learning on a Gaussian mixture model (GMM). Using methods from statistical physics, we compute the asymptotic Bayes risk of each task in the regime of large datasets in high dimension, from which we analyze the role of task similarity in learning and evaluate the performance gain when tasks are learned together rather than separately. In the supervised case, we derive a simple algorithm that attains the Bayes optimal performance.