How transformers learn structured data: insights from hierarchical filtering

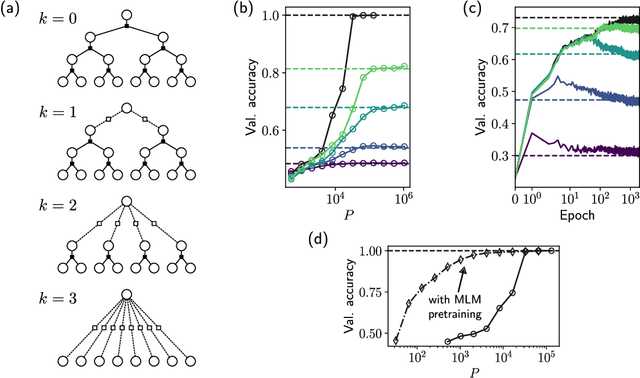
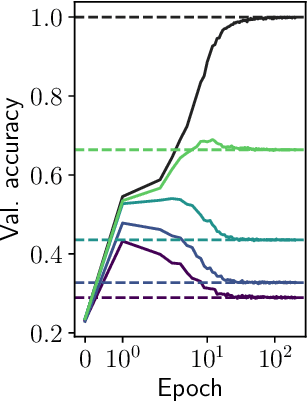
We introduce a hierarchical filtering procedure for generative models of sequences on trees, enabling control over the range of positional correlations in the data. Leveraging this controlled setting, we provide evidence that vanilla encoder-only transformer architectures can implement the optimal Belief Propagation algorithm on both root classification and masked language modeling tasks. Correlations at larger distances corresponding to increasing layers of the hierarchy are sequentially included as the network is trained. We analyze how the transformer layers succeed by focusing on attention maps from models trained with varying degrees of filtering. These attention maps show clear evidence for iterative hierarchical reconstruction of correlations, and we can relate these observations to a plausible implementation of the exact inference algorithm for the network sizes considered.

Kernel Density Estimators in Large Dimensions

This paper studies Kernel density estimation for a high-dimensional distribution $\rho(x)$. Traditional approaches have focused on the limit of large number of data points $n$ and fixed dimension $d$. We analyze instead the regime where both the number $n$ of data points $y_i$ and their dimensionality $d$ grow with a fixed ratio $\alpha=(\log n)/d$. Our study reveals three distinct statistical regimes for the kernel-based estimate of the density $\hat \rho_h^{\mathcal {D}}(x)=\frac{1}{n h^d}\sum_{i=1}^n K\left(\frac{x-y_i}{h}\right)$, depending on the bandwidth $h$: a classical regime for large bandwidth where the Central Limit Theorem (CLT) holds, which is akin to the one found in traditional approaches. Below a certain value of the bandwidth, $h_{CLT}(\alpha)$, we find that the CLT breaks down. The statistics of $\hat \rho_h^{\mathcal {D}}(x)$ for a fixed $x$ drawn from $\rho(x)$ is given by a heavy-tailed distribution (an alpha-stable distribution). In particular below a value $h_G(\alpha)$, we find that $\hat \rho_h^{\mathcal {D}}(x)$ is governed by extreme value statistics: only a few points in the database matter and give the dominant contribution to the density estimator. We provide a detailed analysis for high-dimensional multivariate Gaussian data. We show that the optimal bandwidth threshold based on Kullback-Leibler divergence lies in the new statistical regime identified in this paper. Our findings reveal limitations of classical approaches, show the relevance of these new statistical regimes, and offer new insights for Kernel density estimation in high-dimensional settings.

Dynamical Regimes of Diffusion Models

Using statistical physics methods, we study generative diffusion models in the regime where the dimension of space and the number of data are large, and the score function has been trained optimally. Our analysis reveals three distinct dynamical regimes during the backward generative diffusion process. The generative dynamics, starting from pure noise, encounters first a 'speciation' transition where the gross structure of data is unraveled, through a mechanism similar to symmetry breaking in phase transitions. It is followed at later time by a 'collapse' transition where the trajectories of the dynamics become attracted to one of the memorized data points, through a mechanism which is similar to the condensation in a glass phase. For any dataset, the speciation time can be found from a spectral analysis of the correlation matrix, and the collapse time can be found from the estimation of an 'excess entropy' in the data. The dependence of the collapse time on the dimension and number of data provides a thorough characterization of the curse of dimensionality for diffusion models. Analytical solutions for simple models like high-dimensional Gaussian mixtures substantiate these findings and provide a theoretical framework, while extensions to more complex scenarios and numerical validations with real datasets confirm the theoretical predictions.

The Decimation Scheme for Symmetric Matrix Factorization

Matrix factorization is an inference problem that has acquired importance due to its vast range of applications that go from dictionary learning to recommendation systems and machine learning with deep networks. The study of its fundamental statistical limits represents a true challenge, and despite a decade-long history of efforts in the community, there is still no closed formula able to describe its optimal performances in the case where the rank of the matrix scales linearly with its size. In the present paper, we study this extensive rank problem, extending the alternative 'decimation' procedure that we recently introduced, and carry out a thorough study of its performance. Decimation aims at recovering one column/line of the factors at a time, by mapping the problem into a sequence of neural network models of associative memory at a tunable temperature. Though being sub-optimal, decimation has the advantage of being theoretically analyzable. We extend its scope and analysis to two families of matrices. For a large class of compactly supported priors, we show that the replica symmetric free entropy of the neural network models takes a universal form in the low temperature limit. For sparse Ising prior, we show that the storage capacity of the neural network models diverges as sparsity in the patterns increases, and we introduce a simple algorithm based on a ground state search that implements decimation and performs matrix factorization, with no need of an informative initialization.

Sparse Representations, Inference and Learning

In recent years statistical physics has proven to be a valuable tool to probe into large dimensional inference problems such as the ones occurring in machine learning. Statistical physics provides analytical tools to study fundamental limitations in their solutions and proposes algorithms to solve individual instances. In these notes, based on the lectures by Marc M\'ezard in 2022 at the summer school in Les Houches, we will present a general framework that can be used in a large variety of problems with weak long-range interactions, including the compressed sensing problem, or the problem of learning in a perceptron. We shall see how these problems can be studied at the replica symmetric level, using developments of the cavity methods, both as a theoretical tool and as an algorithm.

Matrix factorization with neural networks

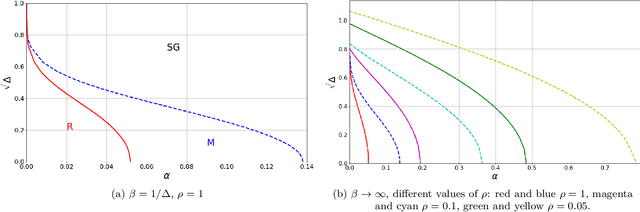
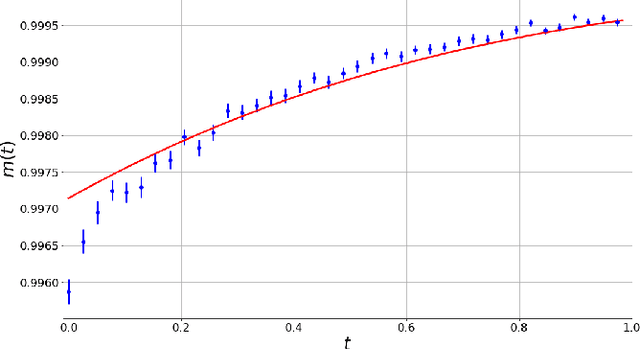
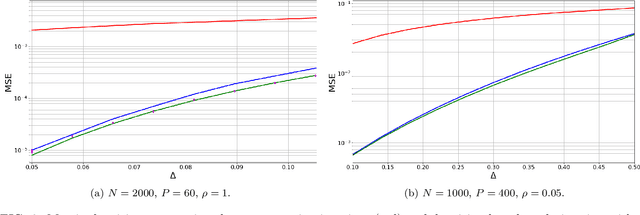
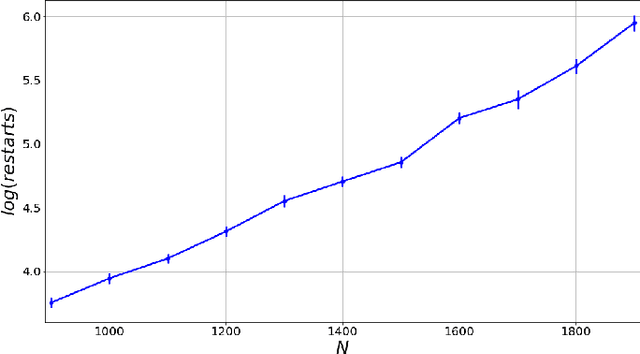
Matrix factorization is an important mathematical problem encountered in the context of dictionary learning, recommendation systems and machine learning. We introduce a new `decimation' scheme that maps it to neural network models of associative memory and provide a detailed theoretical analysis of its performance, showing that decimation is able to factorize extensive-rank matrices and to denoise them efficiently. We introduce a decimation algorithm based on ground-state search of the neural network, which shows performances that match the theoretical prediction.

Capturing the learning curves of generic features maps for realistic data sets with a teacher-student model

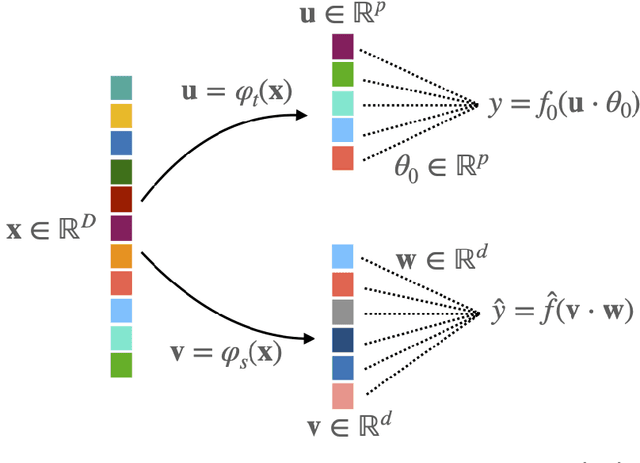
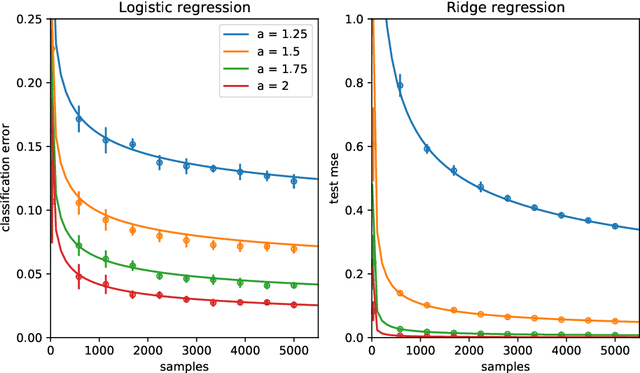
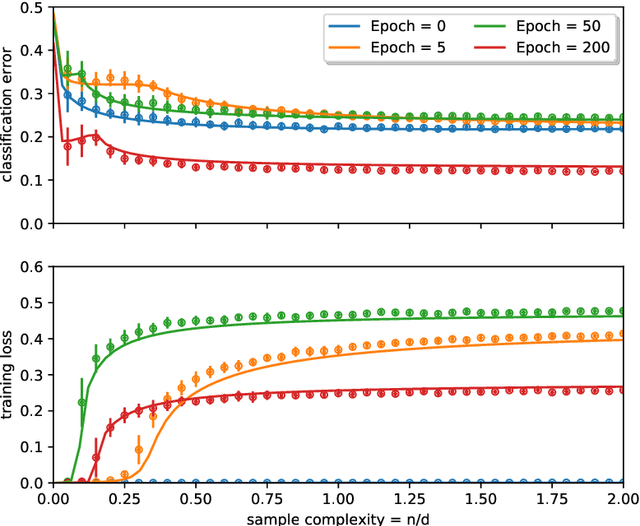
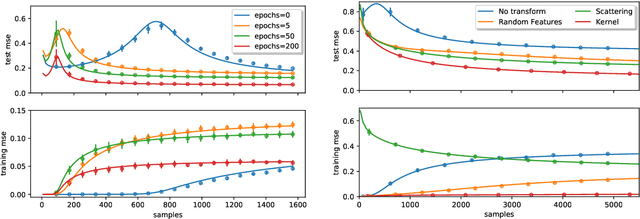
Teacher-student models provide a powerful framework in which the typical case performance of high-dimensional supervised learning tasks can be studied in closed form. In this setting, labels are assigned to data - often taken to be Gaussian i.i.d. - by a teacher model, and the goal is to characterise the typical performance of the student model in recovering the parameters that generated the labels. In this manuscript we discuss a generalisation of this setting where the teacher and student can act on different spaces, generated with fixed, but generic feature maps. This is achieved via the rigorous study of a high-dimensional Gaussian covariate model. Our contribution is two-fold: First, we prove a rigorous formula for the asymptotic training loss and generalisation error achieved by empirical risk minimization for this model. Second, we present a number of situations where the learning curve of the model captures the one of a \emph{realistic data set} learned with kernel regression and classification, with out-of-the-box feature maps such as random projections or scattering transforms, or with pre-learned ones - such as the features learned by training multi-layer neural networks. We discuss both the power and the limitations of the Gaussian teacher-student framework as a typical case analysis capturing learning curves as encountered in practice on real data sets.

Epidemic mitigation by statistical inference from contact tracing data

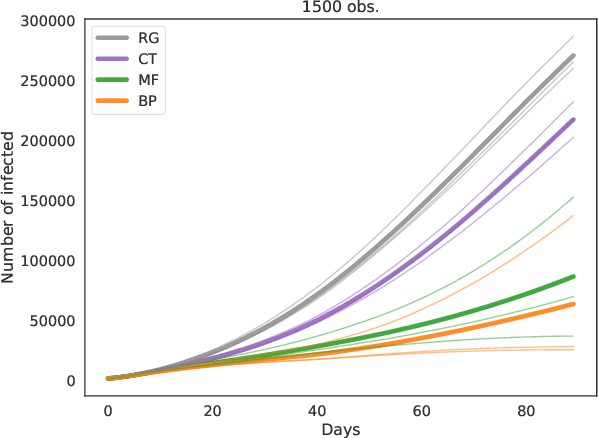
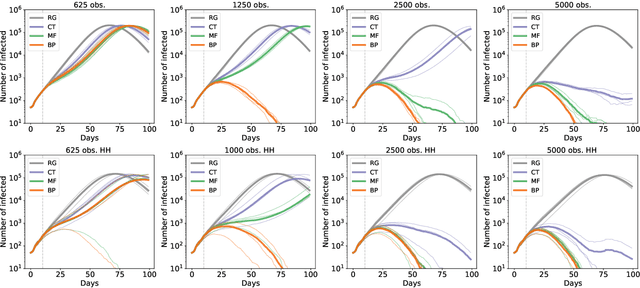
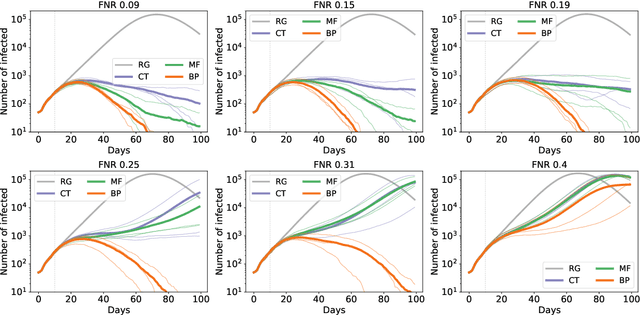
Contact-tracing is an essential tool in order to mitigate the impact of pandemic such as the COVID-19. In order to achieve efficient and scalable contact-tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation in order to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible, but before the fraction of infected people reaches the scale where a lock-down becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized and thus compatible with privacy preserving standards. We conclude that probabilistic risk estimation is capable to enhance performance of digital contact tracing and should be considered in the currently developed mobile applications.

The Gaussian equivalence of generative models for learning with two-layer neural networks

Understanding the impact of data structure on learning in neural networks remains a key challenge for the theory of neural networks. Many theoretical works on neural networks do not explicitly model training data, or assume that inputs are drawn independently from some factorised probability distribution. Here, we go beyond the simple i.i.d. modelling paradigm by studying neural networks trained on data drawn from structured generative models. We make three contributions: First, we establish rigorous conditions under which a class of generative models shares key statistical properties with an appropriately chosen Gaussian feature model. Second, we use this Gaussian equivalence theorem (GET) to derive a closed set of equations that describe the dynamics of two-layer neural networks trained using one-pass stochastic gradient descent on data drawn from a large class of generators. We complement our theoretical results by experiments demonstrating how our theory applies to deep, pre-trained generative models.

Generalisation error in learning with random features and the hidden manifold model

We study generalised linear regression and classification for a synthetically generated dataset encompassing different problems of interest, such as learning with random features, neural networks in the lazy training regime, and the hidden manifold model. We consider the high-dimensional regime and using the replica method from statistical physics, we provide a closed-form expression for the asymptotic generalisation performance in these problems, valid in both the under- and over-parametrised regimes and for a broad choice of generalised linear model loss functions. In particular, we show how to obtain analytically the so-called double descent behaviour for logistic regression with a peak at the interpolation threshold, we illustrate the superiority of orthogonal against random Gaussian projections in learning with random features, and discuss the role played by correlations in the data generated by the hidden manifold model. Beyond the interest in these particular problems, the theoretical formalism introduced in this manuscript provides a path to further extensions to more complex tasks.