On How Iterative Magnitude Pruning Discovers Local Receptive Fields in Fully Connected Neural Networks

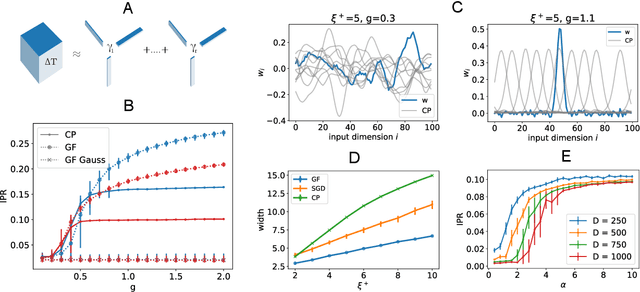
Since its use in the Lottery Ticket Hypothesis, iterative magnitude pruning (IMP) has become a popular method for extracting sparse subnetworks that can be trained to high performance. Despite this, the underlying nature of IMP's general success remains unclear. One possibility is that IMP is especially capable of extracting and maintaining strong inductive biases. In support of this, recent work has shown that applying IMP to fully connected neural networks (FCNs) leads to the emergence of local receptive fields (RFs), an architectural feature present in mammalian visual cortex and convolutional neural networks. The question of how IMP is able to do this remains unanswered. Inspired by results showing that training FCNs on synthetic images with highly non-Gaussian statistics (e.g., sharp edges) is sufficient to drive the formation of local RFs, we hypothesize that IMP iteratively maximizes the non-Gaussian statistics present in the representations of FCNs, creating a feedback loop that enhances localization. We develop a new method for measuring the effect of individual weights on the statistics of the FCN representations ("cavity method"), which allows us to find evidence in support of this hypothesis. Our work, which is the first to study the effect IMP has on the representations of neural networks, sheds parsimonious light one way in which IMP can drive the formation of strong inductive biases.

Feature learning in finite-width Bayesian deep linear networks with multiple outputs and convolutional layers

Deep linear networks have been extensively studied, as they provide simplified models of deep learning. However, little is known in the case of finite-width architectures with multiple outputs and convolutional layers. In this manuscript, we provide rigorous results for the statistics of functions implemented by the aforementioned class of networks, thus moving closer to a complete characterization of feature learning in the Bayesian setting. Our results include: (i) an exact and elementary non-asymptotic integral representation for the joint prior distribution over the outputs, given in terms of a mixture of Gaussians; (ii) an analytical formula for the posterior distribution in the case of squared error loss function (Gaussian likelihood); (iii) a quantitative description of the feature learning infinite-width regime, using large deviation theory. From a physical perspective, deep architectures with multiple outputs or convolutional layers represent different manifestations of kernel shape renormalization, and our work provides a dictionary that translates this physics intuition and terminology into rigorous Bayesian statistics.

Machine learning at the mesoscale: a computation-dissipation bottleneck

The cost of information processing in physical systems calls for a trade-off between performance and energetic expenditure. Here we formulate and study a computation-dissipation bottleneck in mesoscopic systems used as input-output devices. Using both real datasets and synthetic tasks, we show how non-equilibrium leads to enhanced performance. Our framework sheds light on a crucial compromise between information compression, input-output computation and dynamic irreversibility induced by non-reciprocal interactions.

Neural networks trained with SGD learn distributions of increasing complexity

The ability of deep neural networks to generalise well even when they interpolate their training data has been explained using various "simplicity biases". These theories postulate that neural networks avoid overfitting by first learning simple functions, say a linear classifier, before learning more complex, non-linear functions. Meanwhile, data structure is also recognised as a key ingredient for good generalisation, yet its role in simplicity biases is not yet understood. Here, we show that neural networks trained using stochastic gradient descent initially classify their inputs using lower-order input statistics, like mean and covariance, and exploit higher-order statistics only later during training. We first demonstrate this distributional simplicity bias (DSB) in a solvable model of a neural network trained on synthetic data. We empirically demonstrate DSB in a range of deep convolutional networks and visual transformers trained on CIFAR10, and show that it even holds in networks pre-trained on ImageNet. We discuss the relation of DSB to other simplicity biases and consider its implications for the principle of Gaussian universality in learning.

Data-driven emergence of convolutional structure in neural networks

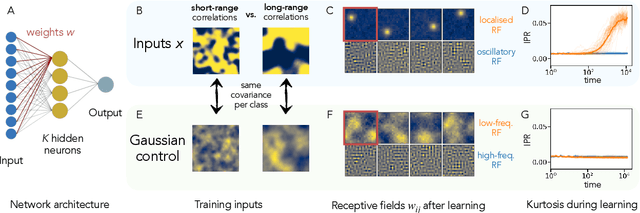
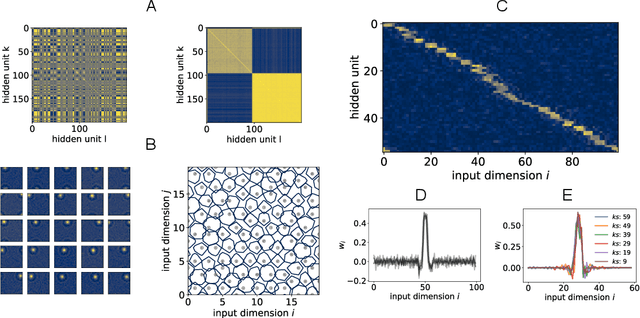
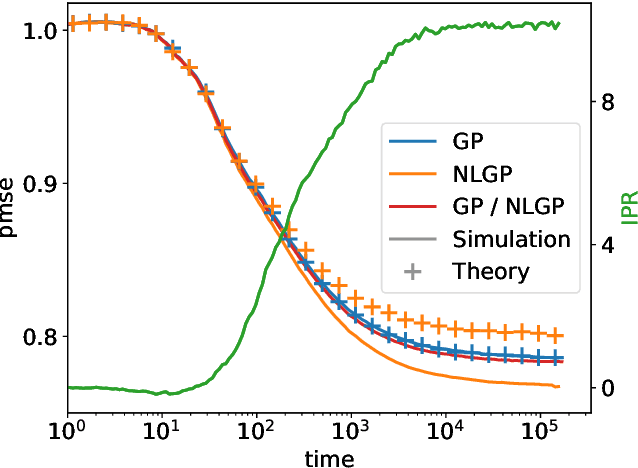
Exploiting data invariances is crucial for efficient learning in both artificial and biological neural circuits. Understanding how neural networks can discover appropriate representations capable of harnessing the underlying symmetries of their inputs is thus crucial in machine learning and neuroscience. Convolutional neural networks, for example, were designed to exploit translation symmetry and their capabilities triggered the first wave of deep learning successes. However, learning convolutions directly from translation-invariant data with a fully-connected network has so far proven elusive. Here, we show how initially fully-connected neural networks solving a discrimination task can learn a convolutional structure directly from their inputs, resulting in localised, space-tiling receptive fields. These receptive fields match the filters of a convolutional network trained on the same task. By carefully designing data models for the visual scene, we show that the emergence of this pattern is triggered by the non-Gaussian, higher-order local structure of the inputs, which has long been recognised as the hallmark of natural images. We provide an analytical and numerical characterisation of the pattern-formation mechanism responsible for this phenomenon in a simple model, which results in an unexpected link between receptive field formation and the tensor decomposition of higher-order input correlations. These results provide a new perspective on the development of low-level feature detectors in various sensory modalities, and pave the way for studying the impact of higher-order statistics on learning in neural networks.

Input correlations impede suppression of chaos and learning in balanced rate networks

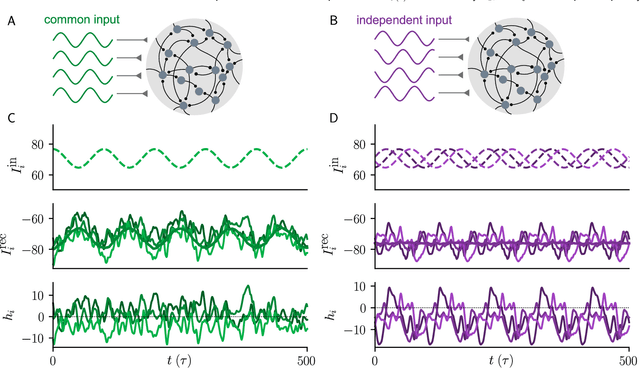
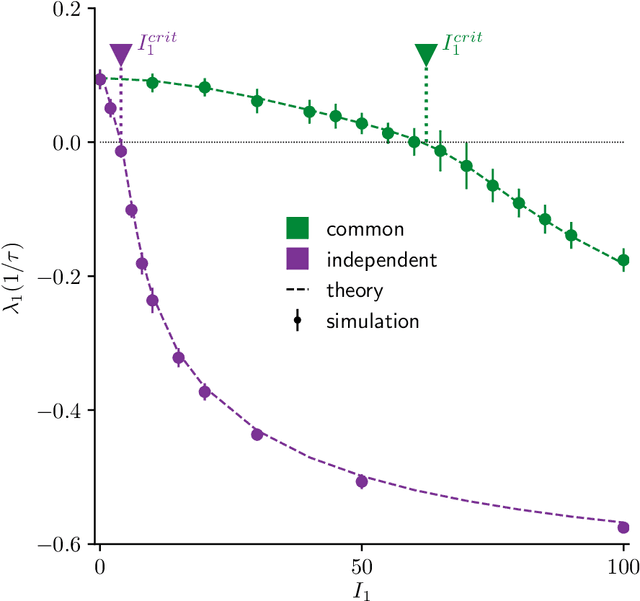
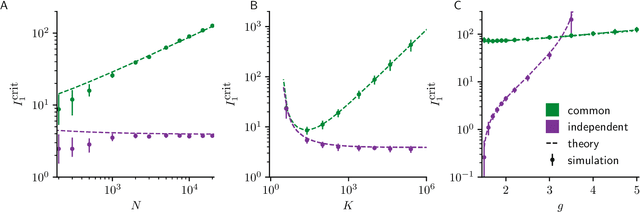
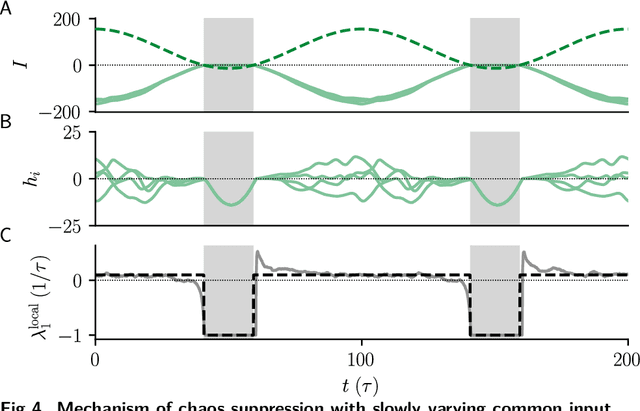
Neural circuits exhibit complex activity patterns, both spontaneously and evoked by external stimuli. Information encoding and learning in neural circuits depend on how well time-varying stimuli can control spontaneous network activity. We show that in firing-rate networks in the balanced state, external control of recurrent dynamics, i.e., the suppression of internally-generated chaotic variability, strongly depends on correlations in the input. A unique feature of balanced networks is that, because common external input is dynamically canceled by recurrent feedback, it is far easier to suppress chaos with independent inputs into each neuron than through common input. To study this phenomenon we develop a non-stationary dynamic mean-field theory that determines how the activity statistics and largest Lyapunov exponent depend on frequency and amplitude of the input, recurrent coupling strength, and network size, for both common and independent input. We also show that uncorrelated inputs facilitate learning in balanced networks.

Epidemic mitigation by statistical inference from contact tracing data

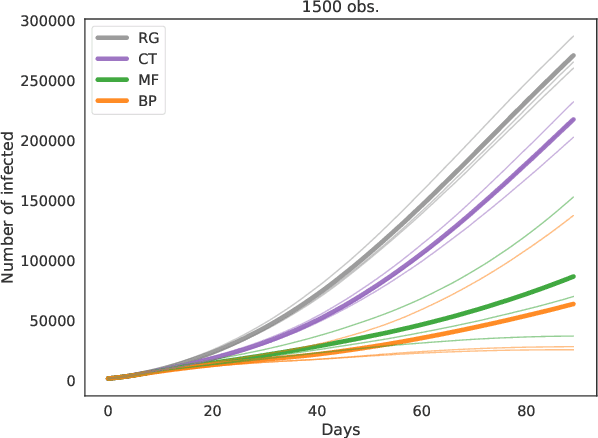
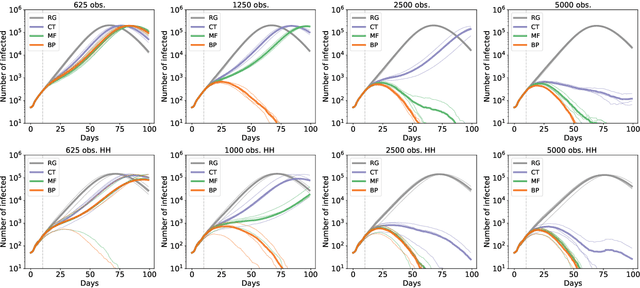
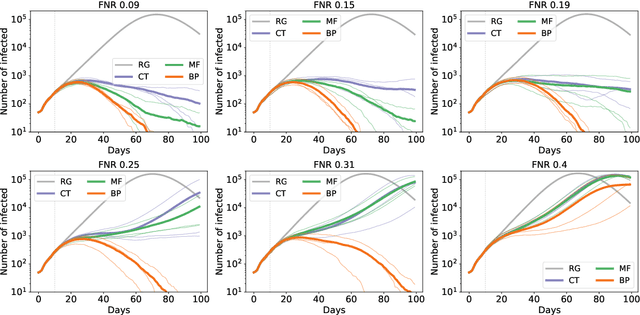
Contact-tracing is an essential tool in order to mitigate the impact of pandemic such as the COVID-19. In order to achieve efficient and scalable contact-tracing in real time, digital devices can play an important role. While a lot of attention has been paid to analyzing the privacy and ethical risks of the associated mobile applications, so far much less research has been devoted to optimizing their performance and assessing their impact on the mitigation of the epidemic. We develop Bayesian inference methods to estimate the risk that an individual is infected. This inference is based on the list of his recent contacts and their own risk levels, as well as personal information such as results of tests or presence of syndromes. We propose to use probabilistic risk estimation in order to optimize testing and quarantining strategies for the control of an epidemic. Our results show that in some range of epidemic spreading (typically when the manual tracing of all contacts of infected people becomes practically impossible, but before the fraction of infected people reaches the scale where a lock-down becomes unavoidable), this inference of individuals at risk could be an efficient way to mitigate the epidemic. Our approaches translate into fully distributed algorithms that only require communication between individuals who have recently been in contact. Such communication may be encrypted and anonymized and thus compatible with privacy preserving standards. We conclude that probabilistic risk estimation is capable to enhance performance of digital contact tracing and should be considered in the currently developed mobile applications.

Optimal Learning with Excitatory and Inhibitory synapses

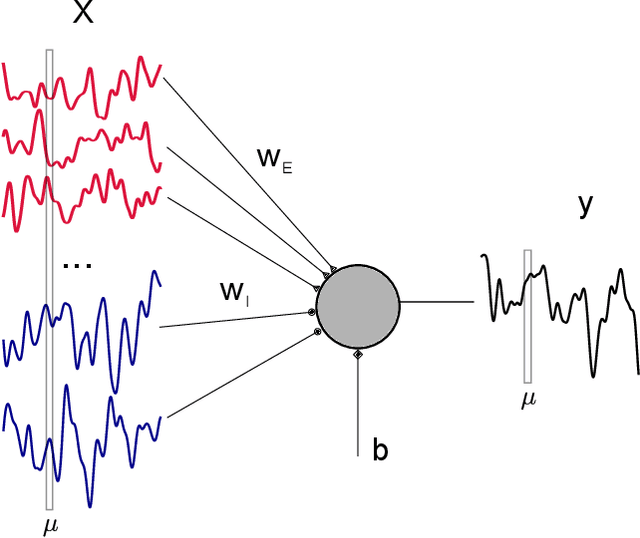
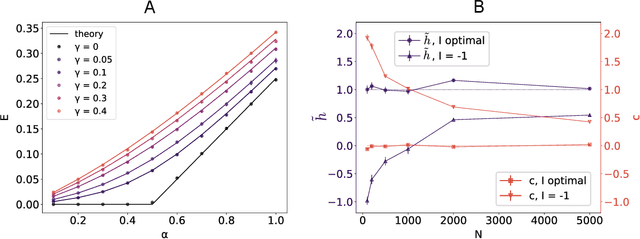
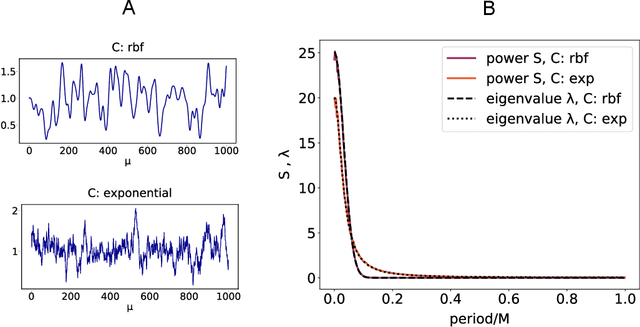
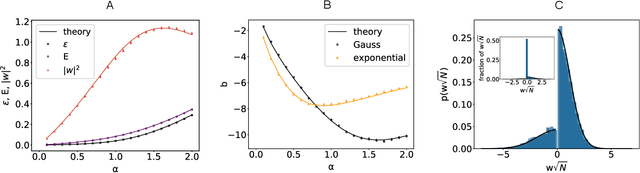
Characterizing the relation between weight structure and input/output statistics is fundamental for understanding the computational capabilities of neural circuits. In this work, I study the problem of storing associations between analog signals in the presence of correlations, using methods from statistical mechanics. I characterize the typical learning performance in terms of the power spectrum of random input and output processes. I show that optimal synaptic weight configurations reach a capacity of 0.5 for any fraction of excitatory to inhibitory weights and have a peculiar synaptic distribution with a finite fraction of silent synapses. I further provide a link between typical learning performance and principal components analysis in single cases. These results may shed light on the synaptic profile of brain circuits, such as cerebellar structures, that are thought to engage in processing time-dependent signals and performing on-line prediction.

Training dynamically balanced excitatory-inhibitory networks

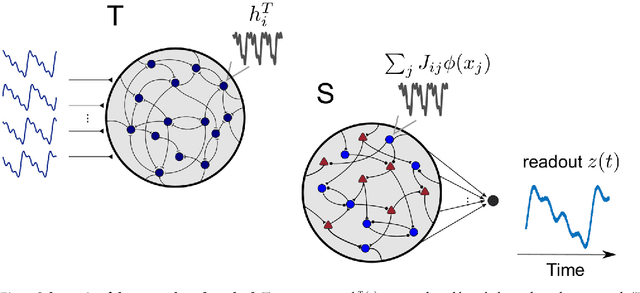
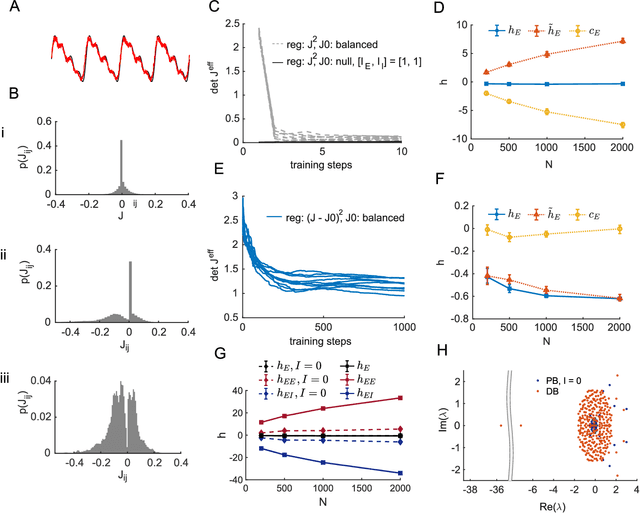
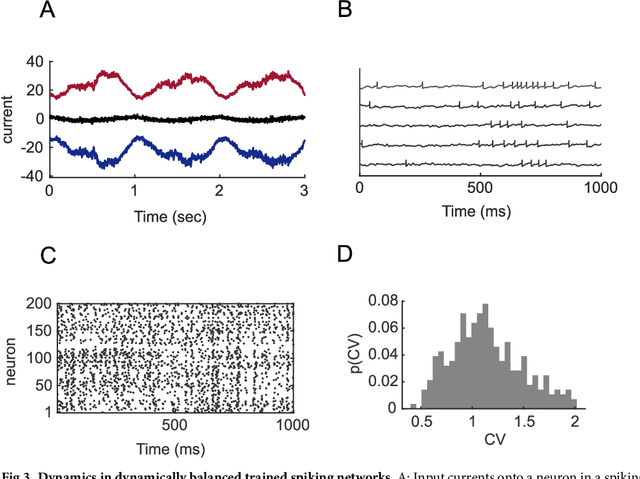
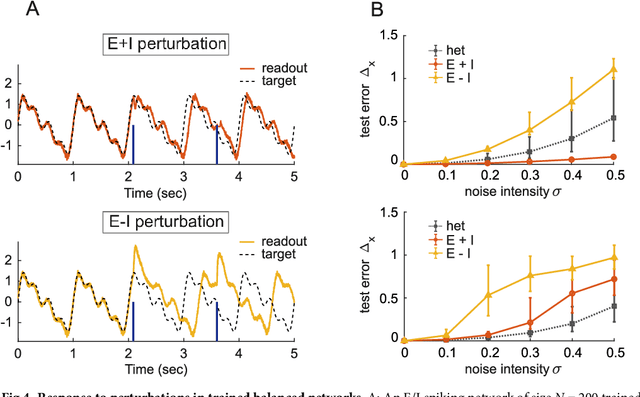
The construction of biologically plausible models of neural circuits is crucial for understanding the computational properties of the nervous system. Constructing functional networks composed of separate excitatory and inhibitory neurons obeying Dale's law presents a number of challenges. We show how a target-based approach, when combined with a fast online constrained optimization technique, is capable of building functional models of rate and spiking recurrent neural networks in which excitation and inhibition are balanced. Balanced networks can be trained to produce complicated temporal patterns and to solve input-output tasks while retaining biologically desirable features such as Dale's law and response variability.

Unreasonable Effectiveness of Learning Neural Networks: From Accessible States and Robust Ensembles to Basic Algorithmic Schemes

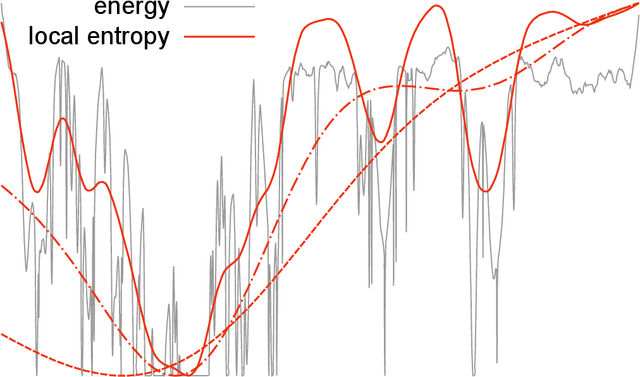
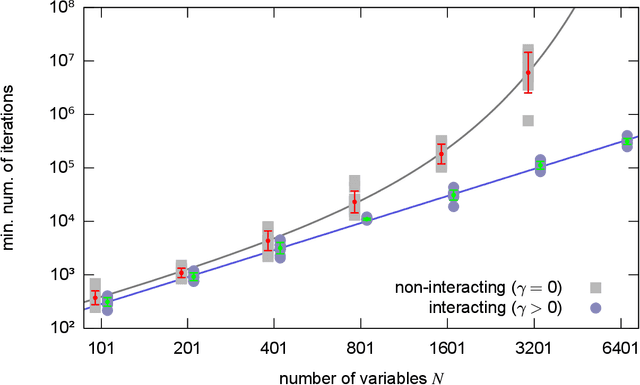
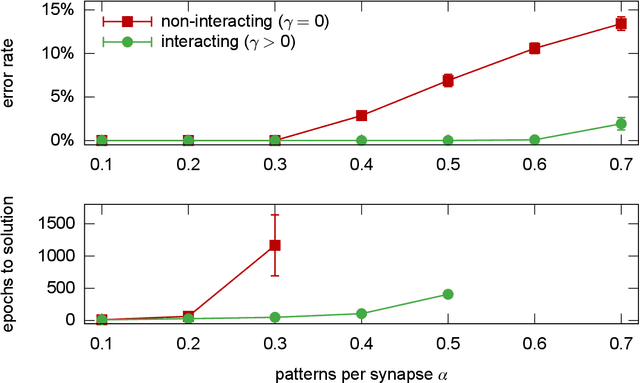
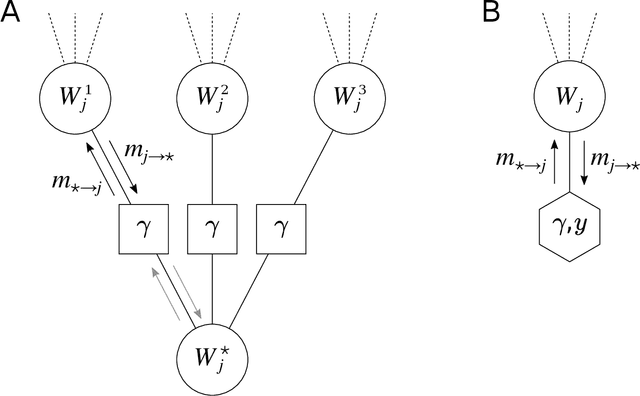
In artificial neural networks, learning from data is a computationally demanding task in which a large number of connection weights are iteratively tuned through stochastic-gradient-based heuristic processes over a cost-function. It is not well understood how learning occurs in these systems, in particular how they avoid getting trapped in configurations with poor computational performance. Here we study the difficult case of networks with discrete weights, where the optimization landscape is very rough even for simple architectures, and provide theoretical and numerical evidence of the existence of rare - but extremely dense and accessible - regions of configurations in the network weight space. We define a novel measure, which we call the "robust ensemble" (RE), which suppresses trapping by isolated configurations and amplifies the role of these dense regions. We analytically compute the RE in some exactly solvable models, and also provide a general algorithmic scheme which is straightforward to implement: define a cost-function given by a sum of a finite number of replicas of the original cost-function, with a constraint centering the replicas around a driving assignment. To illustrate this, we derive several powerful new algorithms, ranging from Markov Chains to message passing to gradient descent processes, where the algorithms target the robust dense states, resulting in substantial improvements in performance. The weak dependence on the number of precision bits of the weights leads us to conjecture that very similar reasoning applies to more conventional neural networks. Analogous algorithmic schemes can also be applied to other optimization problems.