A generalized neural tangent kernel for surrogate gradient learning

State-of-the-art neural network training methods depend on the gradient of the network function. Therefore, they cannot be applied to networks whose activation functions do not have useful derivatives, such as binary and discrete-time spiking neural networks. To overcome this problem, the activation function's derivative is commonly substituted with a surrogate derivative, giving rise to surrogate gradient learning (SGL). This method works well in practice but lacks theoretical foundation. The neural tangent kernel (NTK) has proven successful in the analysis of gradient descent. Here, we provide a generalization of the NTK, which we call the surrogate gradient NTK, that enables the analysis of SGL. First, we study a naive extension of the NTK to activation functions with jumps, demonstrating that gradient descent for such activation functions is also ill-posed in the infinite-width limit. To address this problem, we generalize the NTK to gradient descent with surrogate derivatives, i.e., SGL. We carefully define this generalization and expand the existing key theorems on the NTK with mathematical rigor. Further, we illustrate our findings with numerical experiments. Finally, we numerically compare SGL in networks with sign activation function and finite width to kernel regression with the surrogate gradient NTK; the results confirm that the surrogate gradient NTK provides a good characterization of SGL.

Input correlations impede suppression of chaos and learning in balanced rate networks

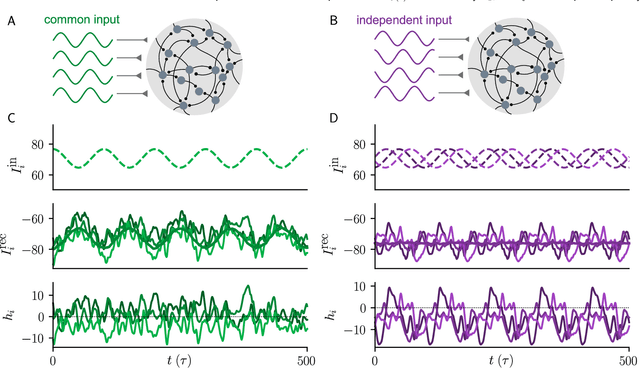
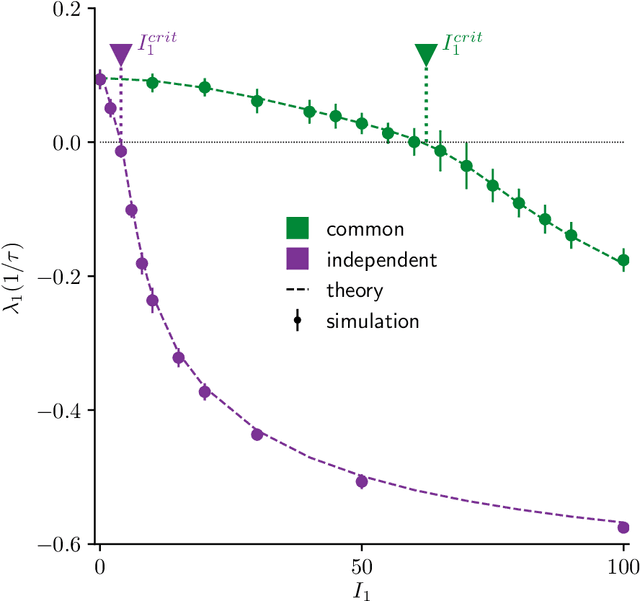
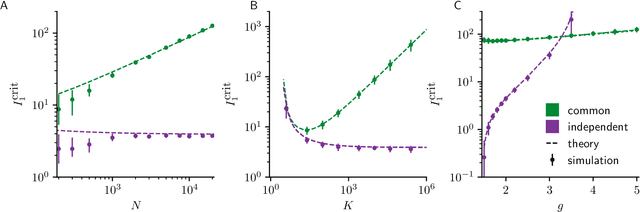
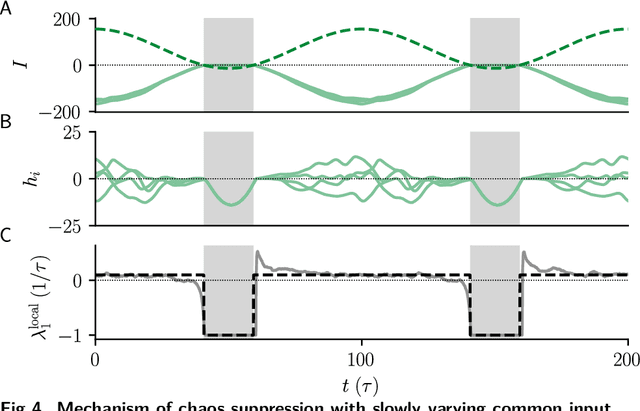
Neural circuits exhibit complex activity patterns, both spontaneously and evoked by external stimuli. Information encoding and learning in neural circuits depend on how well time-varying stimuli can control spontaneous network activity. We show that in firing-rate networks in the balanced state, external control of recurrent dynamics, i.e., the suppression of internally-generated chaotic variability, strongly depends on correlations in the input. A unique feature of balanced networks is that, because common external input is dynamically canceled by recurrent feedback, it is far easier to suppress chaos with independent inputs into each neuron than through common input. To study this phenomenon we develop a non-stationary dynamic mean-field theory that determines how the activity statistics and largest Lyapunov exponent depend on frequency and amplitude of the input, recurrent coupling strength, and network size, for both common and independent input. We also show that uncorrelated inputs facilitate learning in balanced networks.