Sparse chaos in cortical circuits

Nerve impulses, the currency of information flow in the brain, are generated by an instability of the neuronal membrane potential dynamics. Neuronal circuits exhibit collective chaos that appears essential for learning, memory, sensory processing, and motor control. However, the factors controlling the nature and intensity of collective chaos in neuronal circuits are not well understood. Here we use computational ergodic theory to demonstrate that basic features of nerve impulse generation profoundly affect collective chaos in neuronal circuits. Numerically exact calculations of Lyapunov spectra, Kolmogorov-Sinai-entropy, and upper and lower bounds on attractor dimension show that changes in nerve impulse generation in individual neurons moderately impact information encoding rates but qualitatively transform phase space structure. Specifically, we find a drastic reduction in the number of unstable manifolds, Kolmogorov-Sinai entropy, and attractor dimension. Beyond a critical point, marked by the simultaneous breakdown of the diffusion approximation, a peak in the largest Lyapunov exponent, and a localization transition of the leading covariant Lyapunov vector, networks exhibit sparse chaos: prolonged periods of near stable dynamics interrupted by short bursts of intense chaos. Analysis of large, more realistically structured networks supports the generality of these findings. In cortical circuits, biophysical properties appear tuned to this regime of sparse chaos. Our results reveal a close link between fundamental aspects of single-neuron biophysics and the collective dynamics of cortical circuits, suggesting that nerve impulse generation mechanisms are adapted to enhance circuit controllability and information flow.

SparseProp: Efficient Event-Based Simulation and Training of Sparse Recurrent Spiking Neural Networks

Spiking Neural Networks (SNNs) are biologically-inspired models that are capable of processing information in streams of action potentials. However, simulating and training SNNs is computationally expensive due to the need to solve large systems of coupled differential equations. In this paper, we introduce SparseProp, a novel event-based algorithm for simulating and training sparse SNNs. Our algorithm reduces the computational cost of both the forward and backward pass operations from O(N) to O(log(N)) per network spike, thereby enabling numerically exact simulations of large spiking networks and their efficient training using backpropagation through time. By leveraging the sparsity of the network, SparseProp eliminates the need to iterate through all neurons at each spike, employing efficient state updates instead. We demonstrate the efficacy of SparseProp across several classical integrate-and-fire neuron models, including a simulation of a sparse SNN with one million LIF neurons. This results in a speed-up exceeding four orders of magnitude relative to previous event-based implementations. Our work provides an efficient and exact solution for training large-scale spiking neural networks and opens up new possibilities for building more sophisticated brain-inspired models.

Gradient Flossing: Improving Gradient Descent through Dynamic Control of Jacobians

Training recurrent neural networks (RNNs) remains a challenge due to the instability of gradients across long time horizons, which can lead to exploding and vanishing gradients. Recent research has linked these problems to the values of Lyapunov exponents for the forward-dynamics, which describe the growth or shrinkage of infinitesimal perturbations. Here, we propose gradient flossing, a novel approach to tackling gradient instability by pushing Lyapunov exponents of the forward dynamics toward zero during learning. We achieve this by regularizing Lyapunov exponents through backpropagation using differentiable linear algebra. This enables us to "floss" the gradients, stabilizing them and thus improving network training. We demonstrate that gradient flossing controls not only the gradient norm but also the condition number of the long-term Jacobian, facilitating multidimensional error feedback propagation. We find that applying gradient flossing prior to training enhances both the success rate and convergence speed for tasks involving long time horizons. For challenging tasks, we show that gradient flossing during training can further increase the time horizon that can be bridged by backpropagation through time. Moreover, we demonstrate the effectiveness of our approach on various RNN architectures and tasks of variable temporal complexity. Additionally, we provide a simple implementation of our gradient flossing algorithm that can be used in practice. Our results indicate that gradient flossing via regularizing Lyapunov exponents can significantly enhance the effectiveness of RNN training and mitigate the exploding and vanishing gradient problem.

Input correlations impede suppression of chaos and learning in balanced rate networks

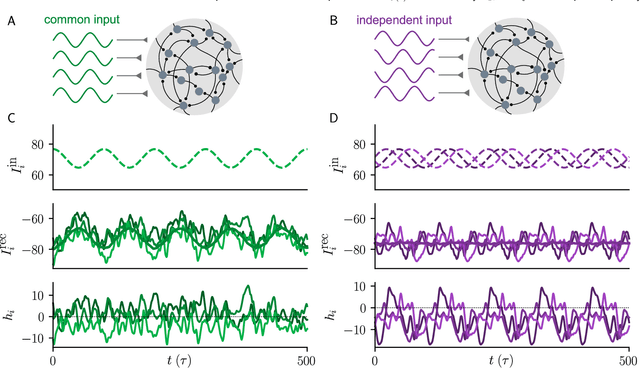
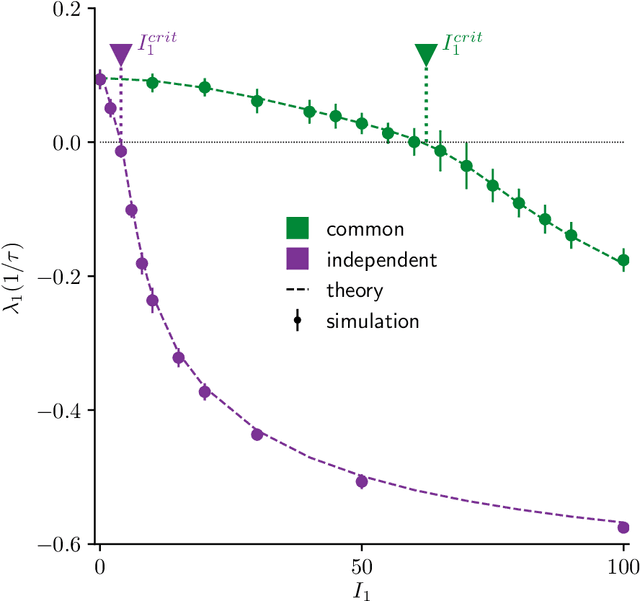
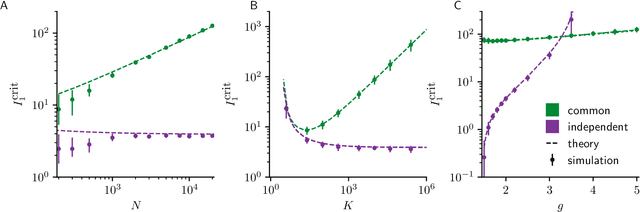
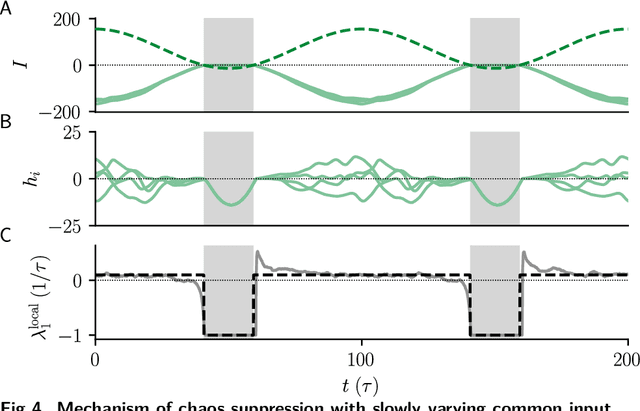
Neural circuits exhibit complex activity patterns, both spontaneously and evoked by external stimuli. Information encoding and learning in neural circuits depend on how well time-varying stimuli can control spontaneous network activity. We show that in firing-rate networks in the balanced state, external control of recurrent dynamics, i.e., the suppression of internally-generated chaotic variability, strongly depends on correlations in the input. A unique feature of balanced networks is that, because common external input is dynamically canceled by recurrent feedback, it is far easier to suppress chaos with independent inputs into each neuron than through common input. To study this phenomenon we develop a non-stationary dynamic mean-field theory that determines how the activity statistics and largest Lyapunov exponent depend on frequency and amplitude of the input, recurrent coupling strength, and network size, for both common and independent input. We also show that uncorrelated inputs facilitate learning in balanced networks.