Ramin Khajeh
Input correlations impede suppression of chaos and learning in balanced rate networks
Jan 24, 2022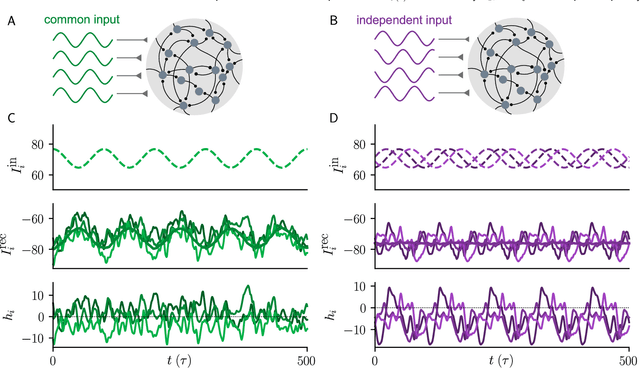
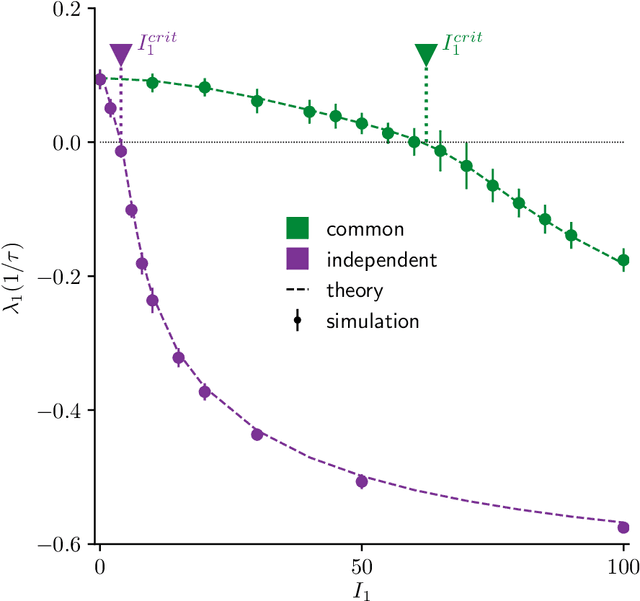
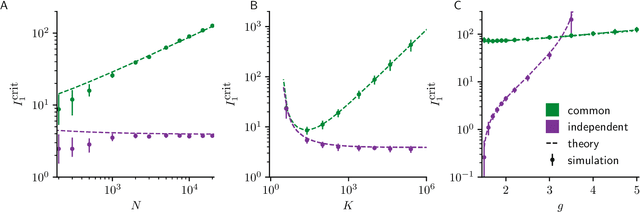
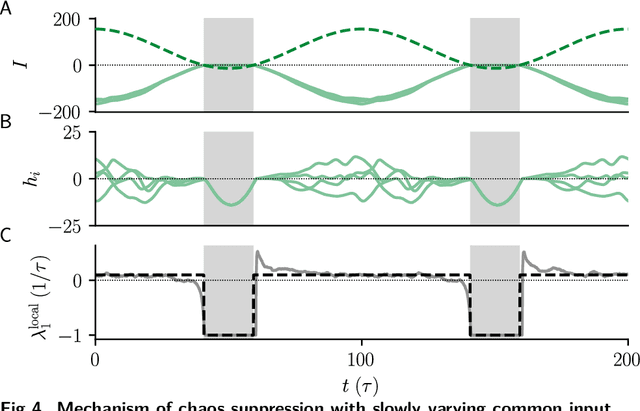
Abstract:Neural circuits exhibit complex activity patterns, both spontaneously and evoked by external stimuli. Information encoding and learning in neural circuits depend on how well time-varying stimuli can control spontaneous network activity. We show that in firing-rate networks in the balanced state, external control of recurrent dynamics, i.e., the suppression of internally-generated chaotic variability, strongly depends on correlations in the input. A unique feature of balanced networks is that, because common external input is dynamically canceled by recurrent feedback, it is far easier to suppress chaos with independent inputs into each neuron than through common input. To study this phenomenon we develop a non-stationary dynamic mean-field theory that determines how the activity statistics and largest Lyapunov exponent depend on frequency and amplitude of the input, recurrent coupling strength, and network size, for both common and independent input. We also show that uncorrelated inputs facilitate learning in balanced networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge