On How Iterative Magnitude Pruning Discovers Local Receptive Fields in Fully Connected Neural Networks

Since its use in the Lottery Ticket Hypothesis, iterative magnitude pruning (IMP) has become a popular method for extracting sparse subnetworks that can be trained to high performance. Despite this, the underlying nature of IMP's general success remains unclear. One possibility is that IMP is especially capable of extracting and maintaining strong inductive biases. In support of this, recent work has shown that applying IMP to fully connected neural networks (FCNs) leads to the emergence of local receptive fields (RFs), an architectural feature present in mammalian visual cortex and convolutional neural networks. The question of how IMP is able to do this remains unanswered. Inspired by results showing that training FCNs on synthetic images with highly non-Gaussian statistics (e.g., sharp edges) is sufficient to drive the formation of local RFs, we hypothesize that IMP iteratively maximizes the non-Gaussian statistics present in the representations of FCNs, creating a feedback loop that enhances localization. We develop a new method for measuring the effect of individual weights on the statistics of the FCN representations ("cavity method"), which allows us to find evidence in support of this hypothesis. Our work, which is the first to study the effect IMP has on the representations of neural networks, sheds parsimonious light one way in which IMP can drive the formation of strong inductive biases.

Koopman Learning with Episodic Memory

Koopman operator theory, a data-driven dynamical systems framework, has found significant success in learning models from complex, real-world data sets, enabling state-of-the-art prediction and control. The greater interpretability and lower computational costs of these models, compared to traditional machine learning methodologies, make Koopman learning an especially appealing approach. Despite this, little work has been performed on endowing Koopman learning with the ability to learn from its own mistakes. To address this, we equip Koopman methods - developed for predicting non-stationary time-series - with an episodic memory mechanism, enabling global recall of (or attention to) periods in time where similar dynamics previously occurred. We find that a basic implementation of Koopman learning with episodic memory leads to significant improvements in prediction on synthetic and real-world data. Our framework has considerable potential for expansion, allowing for future advances, and opens exciting new directions for Koopman learning.

On Equivalent Optimization of Machine Learning Methods

At the core of many machine learning methods resides an iterative optimization algorithm for their training. Such optimization algorithms often come with a plethora of choices regarding their implementation. In the case of deep neural networks, choices of optimizer, learning rate, batch size, etc. must be made. Despite the fundamental way in which these choices impact the training of deep neural networks, there exists no general method for identifying when they lead to equivalent, or non-equivalent, optimization trajectories. By viewing iterative optimization as a discrete-time dynamical system, we are able to leverage Koopman operator theory, where it is known that conjugate dynamics can have identical spectral objects. We find highly overlapping Koopman spectra associated with the application of online mirror and gradient descent to specific problems, illustrating that such a data-driven approach can corroborate the recently discovered analytical equivalence between the two optimizers. We extend our analysis to feedforward, fully connected neural networks, providing the first general characterization of when choices of learning rate, batch size, layer width, data set, and activation function lead to equivalent, and non-equivalent, evolution of network parameters during training. Among our main results, we find that learning rate to batch size ratio, layer width, nature of data set (handwritten vs. synthetic), and activation function affect the nature of conjugacy. Our data-driven approach is general and can be utilized broadly to compare the optimization of machine learning methods.

An Operator Theoretic Perspective on Pruning Deep Neural Networks

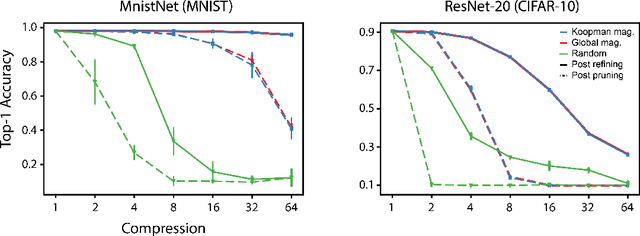
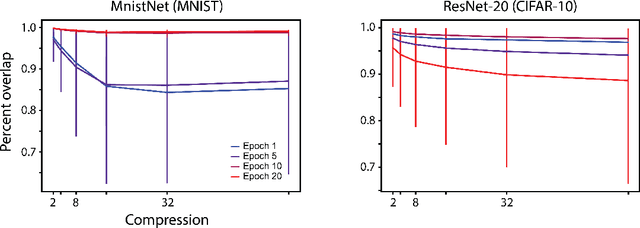
The discovery of sparse subnetworks that are able to perform as well as full models has found broad applied and theoretical interest. While many pruning methods have been developed to this end, the na\"ive approach of removing parameters based on their magnitude has been found to be as robust as more complex, state-of-the-art algorithms. The lack of theory behind magnitude pruning's success, especially pre-convergence, and its relation to other pruning methods, such as gradient based pruning, are outstanding open questions in the field that are in need of being addressed. We make use of recent advances in dynamical systems theory, namely Koopman operator theory, to define a new class of theoretically motivated pruning algorithms. We show that these algorithms can be equivalent to magnitude and gradient based pruning, unifying these seemingly disparate methods, and that they can be used to shed light on magnitude pruning's performance during early training.

Universality of Deep Neural Network Lottery Tickets: A Renormalization Group Perspective

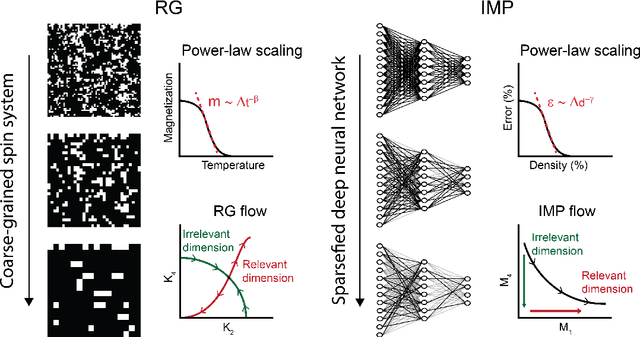
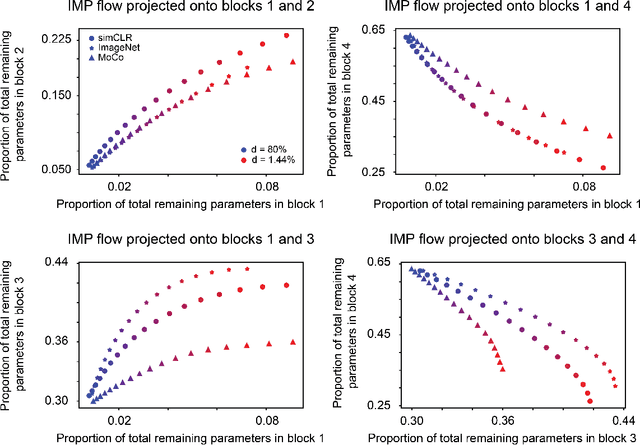
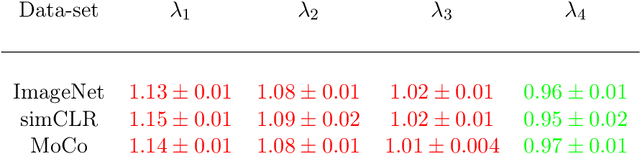
Foundational work on the Lottery Ticket Hypothesis has suggested an exciting corollary: winning tickets found in the context of one task can be transferred to similar tasks, possibly even across different architectures. While this has become of broad practical and theoretical interest, to date, there exists no detailed understanding of why winning ticket universality exists, or any way of knowing \textit{a priori} whether a given ticket can be transferred to a given task. To address these outstanding open questions, we make use of renormalization group theory, one of the most successful tools in theoretical physics. We find that iterative magnitude pruning, the method used for discovering winning tickets, is a renormalization group scheme. This opens the door to a wealth of existing numerical and theoretical tools, some of which we leverage here to examine winning ticket universality in large scale lottery ticket experiments, as well as sheds new light on the success iterative magnitude pruning has found in the field of sparse machine learning.