Universality of Deep Neural Network Lottery Tickets: A Renormalization Group Perspective

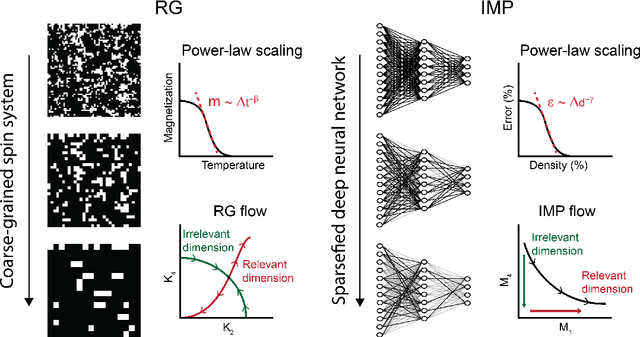
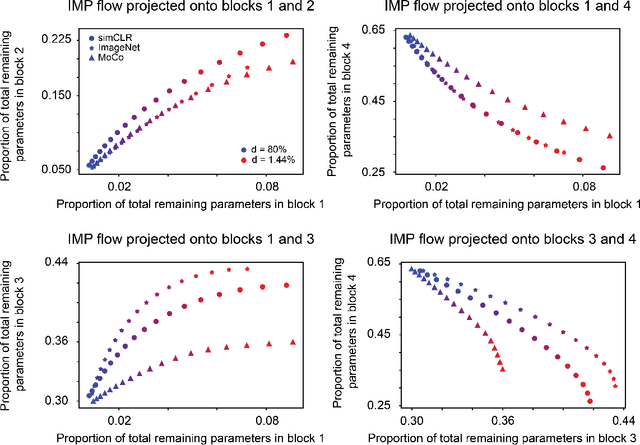
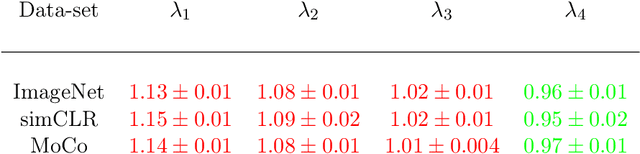
Foundational work on the Lottery Ticket Hypothesis has suggested an exciting corollary: winning tickets found in the context of one task can be transferred to similar tasks, possibly even across different architectures. While this has become of broad practical and theoretical interest, to date, there exists no detailed understanding of why winning ticket universality exists, or any way of knowing \textit{a priori} whether a given ticket can be transferred to a given task. To address these outstanding open questions, we make use of renormalization group theory, one of the most successful tools in theoretical physics. We find that iterative magnitude pruning, the method used for discovering winning tickets, is a renormalization group scheme. This opens the door to a wealth of existing numerical and theoretical tools, some of which we leverage here to examine winning ticket universality in large scale lottery ticket experiments, as well as sheds new light on the success iterative magnitude pruning has found in the field of sparse machine learning.

Local error quantification for efficient neural network dynamical system solvers

Neural Networks have been identified as powerful tools for the study of complex systems. A noteworthy example is the Neural Network Differential Equation (NN DE) solver, which can provide functional approximations to the solutions of a wide variety of differential equations. However, there is a lack of work on the role precise error quantification can play in their predictions: most variants focus on ambiguous and/or global measures of performance like the loss function. We address this in the context of dynamical system NN DE solvers, leveraging their \textit{learnt} information to develop more accurate and efficient solvers, while still pursuing an unsupervised approach that does not rely on external tools or data. We achieve this via methods that precisely quantify NN DE solver errors at local scales, thus allowing the user the capacity for efficient and targeted error correction. We exemplify the utility of our methods by testing them on a nonlinear and a chaotic system each.

A blueprint for building efficient Neural Network Differential Equation Solvers

Neural Networks are well known to have universal approximation properties for wide classes of Lebesgue integrable functions. We describe a collection of strategies and applications sourced from various fields of mathematics and physics to detail a rough blueprint for building efficient Neural Network differential equation solvers.

Optimizing Neural Networks via Koopman Operator Theory

Koopman operator theory, a powerful framework for discovering the underlying dynamics of nonlinear dynamical systems, was recently shown to be intimately connected with neural network training. In this work, we take the first steps in making use of this connection. As Koopman operator theory is a linear theory, a successful implementation of it in evolving network weights and biases offers the promise of accelerated training, especially in the context of deep networks, where optimization is inherently a non-convex problem. We show that Koopman operator theory methods allow for accurate predictions of the weights and biases of a feedforward, fully connected deep network over a non-trivial range of training time. During this time window, we find that our approach is at least 10x faster than gradient descent based methods, in line with the results expected from our complexity analysis. We highlight additional methods by which our results can be expanded to broader classes of networks and larger time intervals, which shall be the focus of future work in this novel intersection between dynamical systems and neural network theory.

Hamiltonian Neural Networks for solving differential equations

There has been a wave of interest in applying machine learning to study dynamical systems. In particular, neural networks have been applied to solve the equations of motion, and therefore, track the evolution of a system. In contrast to other applications of neural networks and machine learning, dynamical systems -- depending on their underlying symmetries -- possess invariants such as energy, momentum, and angular momentum. Traditional numerical iteration methods usually violate these conservation laws, propagating errors in time, and reducing the predictability of the method. We present a Hamiltonian neural network that solves the differential equations that govern dynamical systems. This unsupervised model is learning solutions that satisfy identically, up to an arbitrarily small error, Hamilton's equations and, therefore, conserve the Hamiltonian invariants. Once it is optimized, the proposed architecture is considered a symplectic unit due to the introduction of an efficient parametric form of solutions. In addition, by sharing the network parameters and the choice of an appropriate activation function drastically improve the predictability of the network. An error analysis is derived and states that the numerical errors depend on the overall network performance. The symplectic architecture is then employed to solve the equations for the nonlinear oscillator and the chaotic Henon-Heiles dynamical system. In both systems, the symplectic Euler integrator requires two orders more evaluation points than the Hamiltonian network in order to achieve the same order of the numerical error in the predicted phase space trajectories.