First principles physics-informed neural network for quantum wavefunctions and eigenvalue surfaces

Physics-informed neural networks have been widely applied to learn general parametric solutions of differential equations. Here, we propose a neural network to discover parametric eigenvalue and eigenfunction surfaces of quantum systems. We apply our method to solve the hydrogen molecular ion. This is an ab-initio deep learning method that solves the Schrodinger equation with the Coulomb potential yielding realistic wavefunctions that include a cusp at the ion positions. The neural solutions are continuous and differentiable functions of the interatomic distance and their derivatives are analytically calculated by applying automatic differentiation. Such a parametric and analytical form of the solutions is useful for further calculations such as the determination of force fields.

Transfer Learning with Physics-Informed Neural Networks for Efficient Simulation of Branched Flows

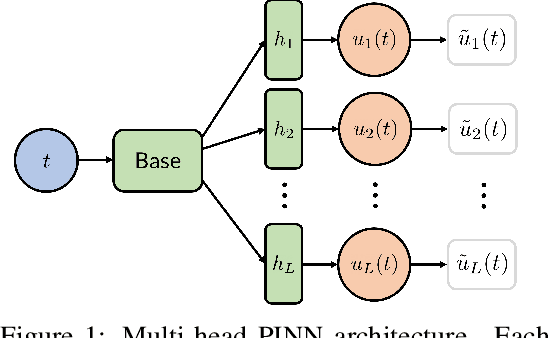
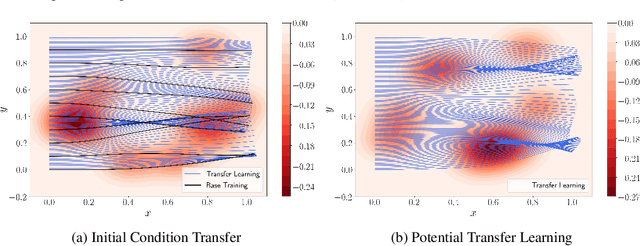
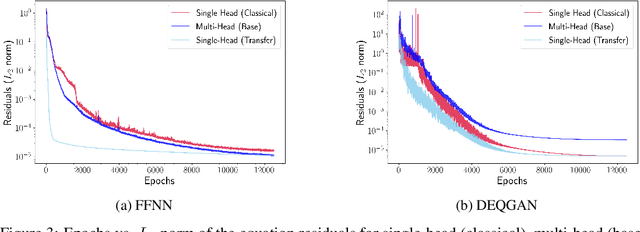
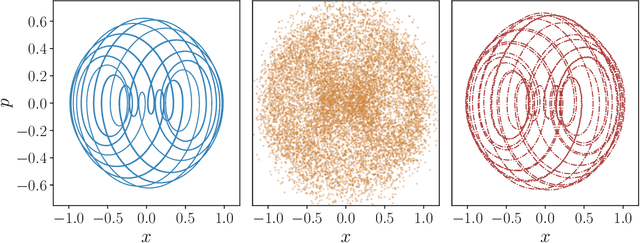
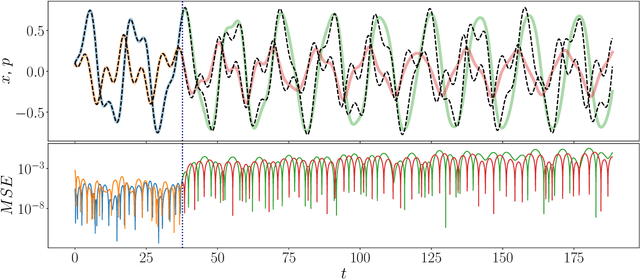
Physics-Informed Neural Networks (PINNs) offer a promising approach to solving differential equations and, more generally, to applying deep learning to problems in the physical sciences. We adopt a recently developed transfer learning approach for PINNs and introduce a multi-head model to efficiently obtain accurate solutions to nonlinear systems of ordinary differential equations with random potentials. In particular, we apply the method to simulate stochastic branched flows, a universal phenomenon in random wave dynamics. Finally, we compare the results achieved by feed forward and GAN-based PINNs on two physically relevant transfer learning tasks and show that our methods provide significant computational speedups in comparison to standard PINNs trained from scratch.

RcTorch: a PyTorch Reservoir Computing Package with Automated Hyper-Parameter Optimization

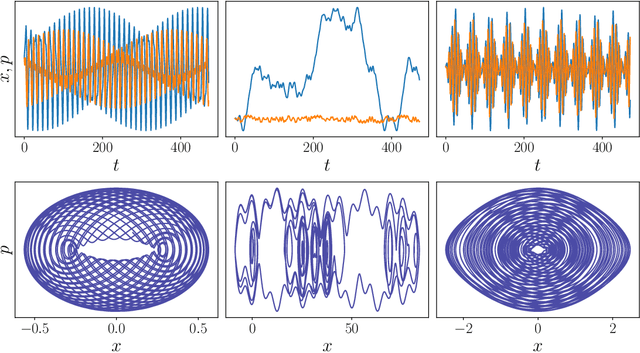
Reservoir computers (RCs) are among the fastest to train of all neural networks, especially when they are compared to other recurrent neural networks. RC has this advantage while still handling sequential data exceptionally well. However, RC adoption has lagged other neural network models because of the model's sensitivity to its hyper-parameters (HPs). A modern unified software package that automatically tunes these parameters is missing from the literature. Manually tuning these numbers is very difficult, and the cost of traditional grid search methods grows exponentially with the number of HPs considered, discouraging the use of the RC and limiting the complexity of the RC models which can be devised. We address these problems by introducing RcTorch, a PyTorch based RC neural network package with automated HP tuning. Herein, we demonstrate the utility of RcTorch by using it to predict the complex dynamics of a driven pendulum being acted upon by varying forces. This work includes coding examples. Example Python Jupyter notebooks can be found on our GitHub repository https://github.com/blindedjoy/RcTorch and documentation can be found at https://rctorch.readthedocs.io/.

Physics-Informed Neural Networks for Quantum Eigenvalue Problems

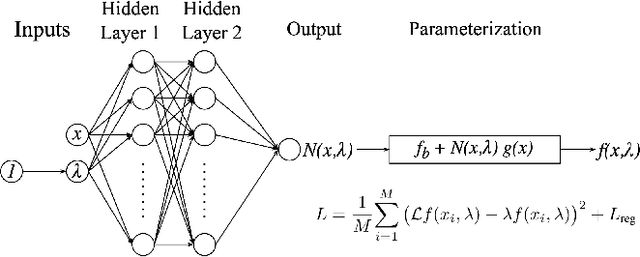
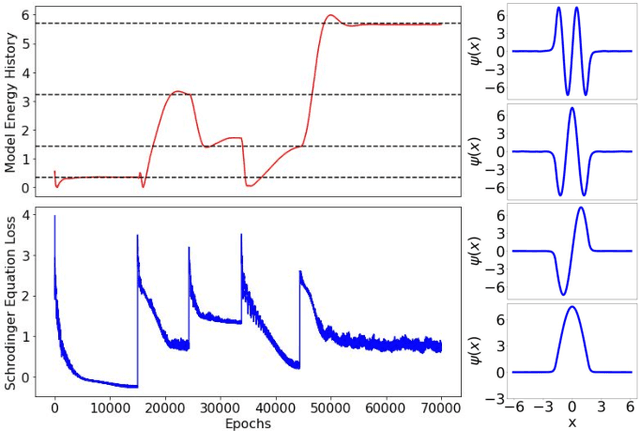
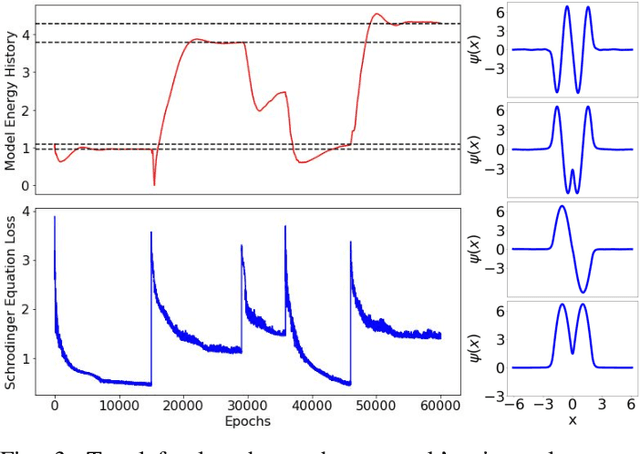
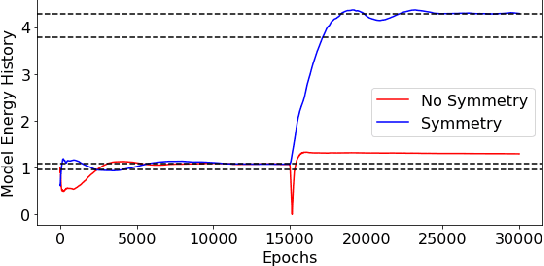
Eigenvalue problems are critical to several fields of science and engineering. We expand on the method of using unsupervised neural networks for discovering eigenfunctions and eigenvalues for differential eigenvalue problems. The obtained solutions are given in an analytical and differentiable form that identically satisfies the desired boundary conditions. The network optimization is data-free and depends solely on the predictions of the neural network. We introduce two physics-informed loss functions. The first, called ortho-loss, motivates the network to discover pair-wise orthogonal eigenfunctions. The second loss term, called norm-loss, requests the discovery of normalized eigenfunctions and is used to avoid trivial solutions. We find that embedding even or odd symmetries to the neural network architecture further improves the convergence for relevant problems. Lastly, a patience condition can be used to automatically recognize eigenfunction solutions. This proposed unsupervised learning method is used to solve the finite well, multiple finite wells, and hydrogen atom eigenvalue quantum problems.

One-Shot Transfer Learning of Physics-Informed Neural Networks

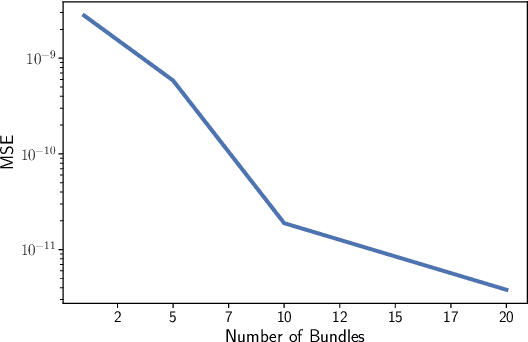
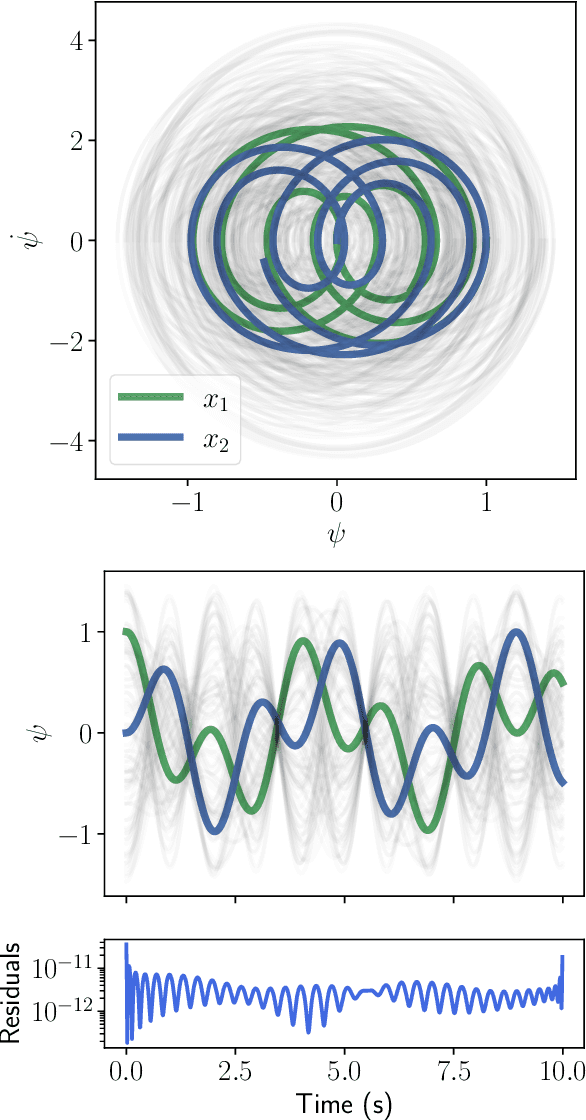
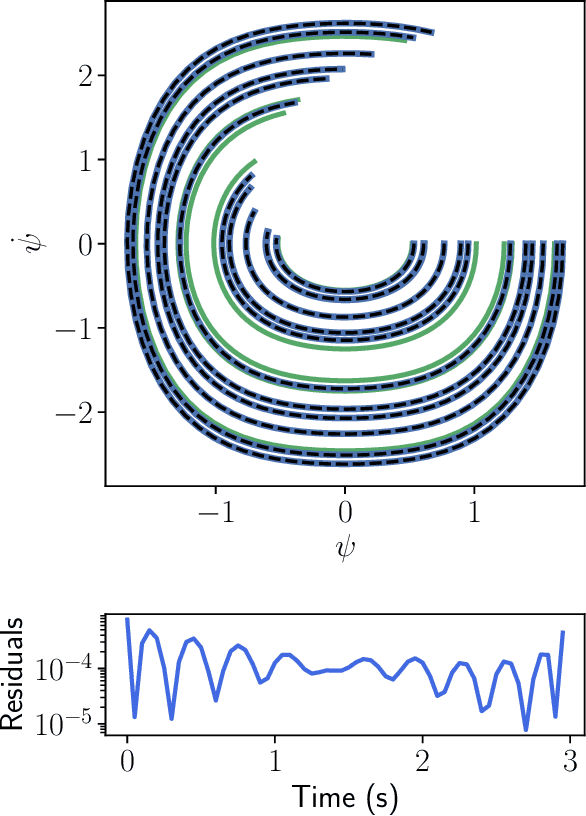
Solving differential equations efficiently and accurately sits at the heart of progress in many areas of scientific research, from classical dynamical systems to quantum mechanics. There is a surge of interest in using Physics-Informed Neural Networks (PINNs) to tackle such problems as they provide numerous benefits over traditional numerical approaches. Despite their potential benefits for solving differential equations, transfer learning has been under explored. In this study, we present a general framework for transfer learning PINNs that results in one-shot inference for linear systems of both ordinary and partial differential equations. This means that highly accurate solutions to many unknown differential equations can be obtained instantaneously without retraining an entire network. We demonstrate the efficacy of the proposed deep learning approach by solving several real-world problems, such as first- and second-order linear ordinary equations, the Poisson equation, and the time-dependent Schrodinger complex-value partial differential equation.

Modeling the effect of the vaccination campaign on the Covid-19 pandemic

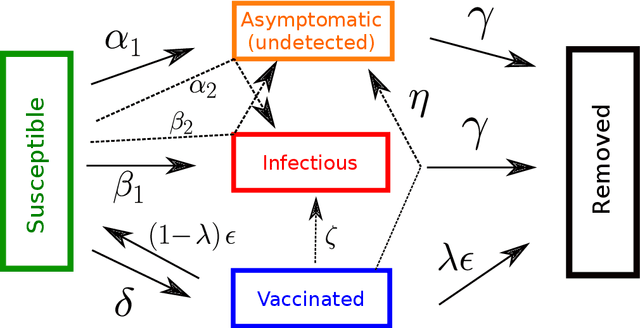
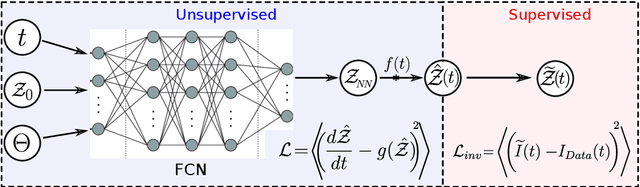
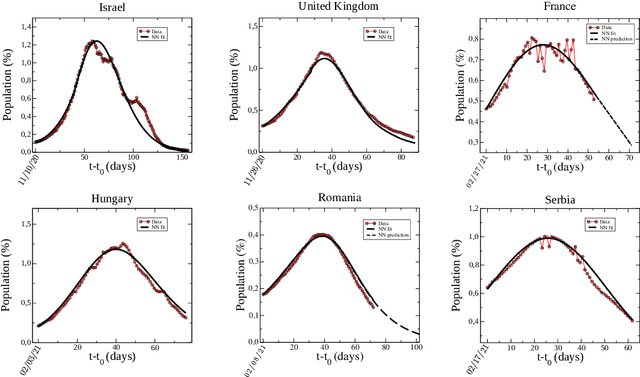
Population-wide vaccination is critical for containing the SARS-CoV-2 (Covid-19) pandemic when combined with restrictive and prevention measures. In this study, we introduce SAIVR, a mathematical model able to forecast the Covid-19 epidemic evolution during the vaccination campaign. SAIVR extends the widely used Susceptible-Infectious-Removed (SIR) model by considering the Asymptomatic (A) and Vaccinated (V) compartments. The model contains several parameters and initial conditions that are estimated by employing a semi-supervised machine learning procedure. After training an unsupervised neural network to solve the SAIVR differential equations, a supervised framework then estimates the optimal conditions and parameters that best fit recent infectious curves of 27 countries. Instructed by these results, we performed an extensive study on the temporal evolution of the pandemic under varying values of roll-out daily rates, vaccine efficacy, and a broad range of societal vaccine hesitancy/denial levels. The concept of herd immunity is questioned by studying future scenarios which involve different vaccination efforts and more infectious Covid-19 variants.

Unsupervised Reservoir Computing for Solving Ordinary Differential Equations

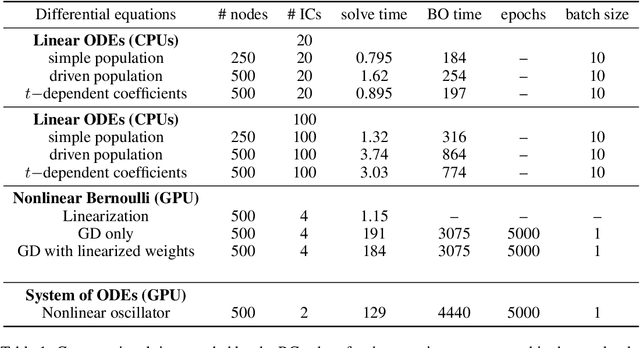
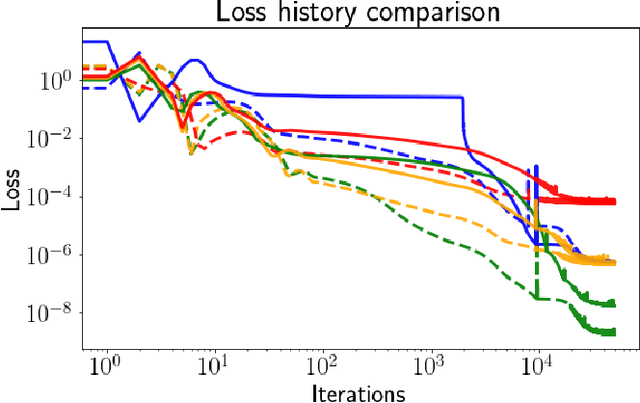
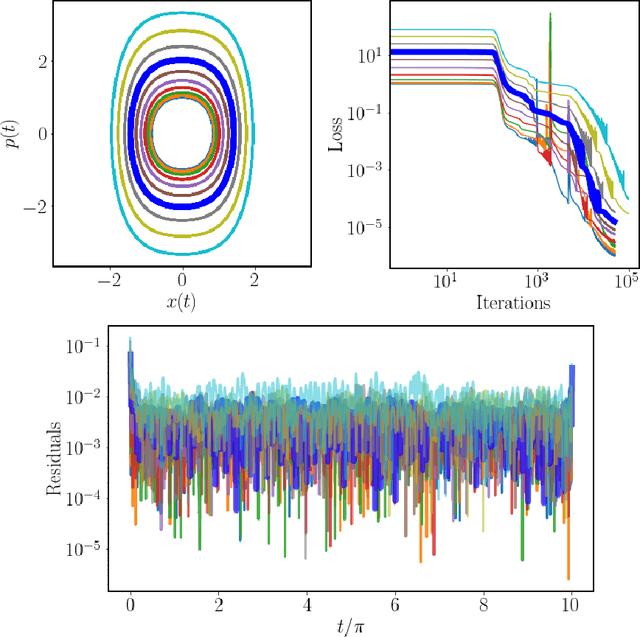
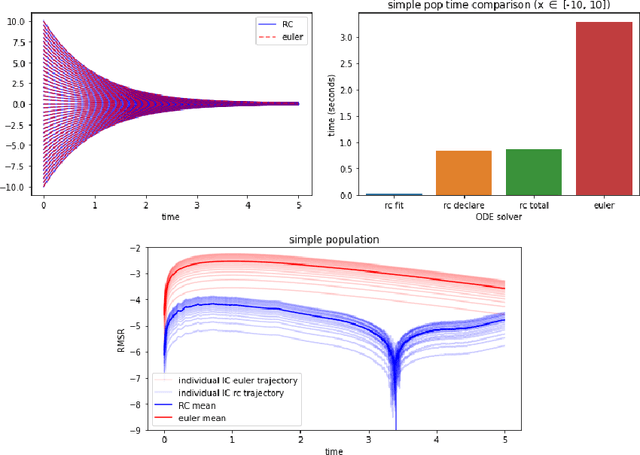
There is a wave of interest in using unsupervised neural networks for solving differential equations. The existing methods are based on feed-forward networks, {while} recurrent neural network differential equation solvers have not yet been reported. We introduce an unsupervised reservoir computing (RC), an echo-state recurrent neural network capable of discovering approximate solutions that satisfy ordinary differential equations (ODEs). We suggest an approach to calculate time derivatives of recurrent neural network outputs without using backpropagation. The internal weights of an RC are fixed, while only a linear output layer is trained, yielding efficient training. However, RC performance strongly depends on finding the optimal hyper-parameters, which is a computationally expensive process. We use Bayesian optimization to efficiently discover optimal sets in a high-dimensional hyper-parameter space and numerically show that one set is robust and can be used to solve an ODE for different initial conditions and time ranges. A closed-form formula for the optimal output weights is derived to solve first order linear equations in a backpropagation-free learning process. We extend the RC approach by solving nonlinear system of ODEs using a hybrid optimization method consisting of gradient descent and Bayesian optimization. Evaluation of linear and nonlinear systems of equations demonstrates the efficiency of the RC ODE solver.

Port-Hamiltonian Neural Networks for Learning Explicit Time-Dependent Dynamical Systems

Accurately learning the temporal behavior of dynamical systems requires models with well-chosen learning biases. Recent innovations embed the Hamiltonian and Lagrangian formalisms into neural networks and demonstrate a significant improvement over other approaches in predicting trajectories of physical systems. These methods generally tackle autonomous systems that depend implicitly on time or systems for which a control signal is known apriori. Despite this success, many real world dynamical systems are non-autonomous, driven by time-dependent forces and experience energy dissipation. In this study, we address the challenge of learning from such non-autonomous systems by embedding the port-Hamiltonian formalism into neural networks, a versatile framework that can capture energy dissipation and time-dependent control forces. We show that the proposed \emph{port-Hamiltonian neural network} can efficiently learn the dynamics of nonlinear physical systems of practical interest and accurately recover the underlying stationary Hamiltonian, time-dependent force, and dissipative coefficient. A promising outcome of our network is its ability to learn and predict chaotic systems such as the Duffing equation, for which the trajectories are typically hard to learn.

Encoding Involutory Invariance in Neural Networks

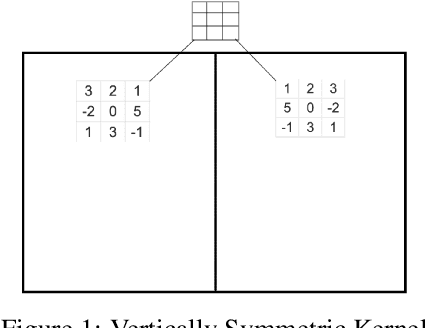
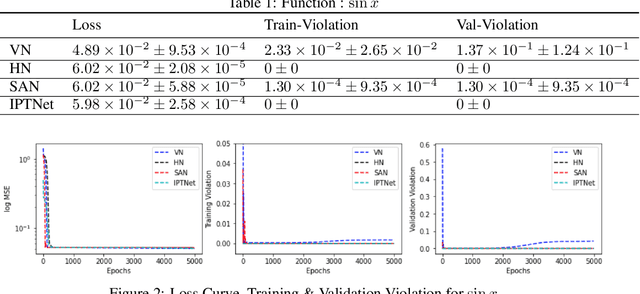
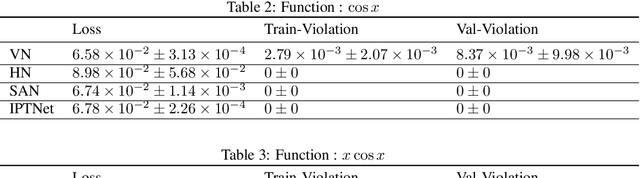
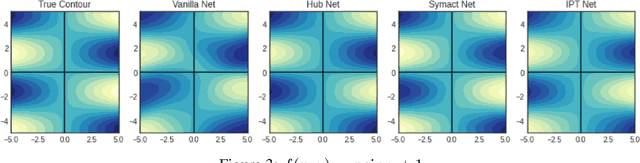
In certain situations, Neural Networks (NN) are trained upon data that obey underlying physical symmetries. However, it is not guaranteed that NNs will obey the underlying symmetry unless embedded in the network structure. In this work, we explore a special kind of symmetry where functions are invariant with respect to involutory linear/affine transformations up to parity $p=\pm 1$. We develop mathematical theorems and propose NN architectures that ensure invariance and universal approximation properties. Numerical experiments indicate that the proposed models outperform baseline networks while respecting the imposed symmetry. An adaption of our technique to convolutional NN classification tasks for datasets with inherent horizontal/vertical reflection symmetry has also been proposed.

A New Artificial Neuron Proposal with Trainable Simultaneous Local and Global Activation Function

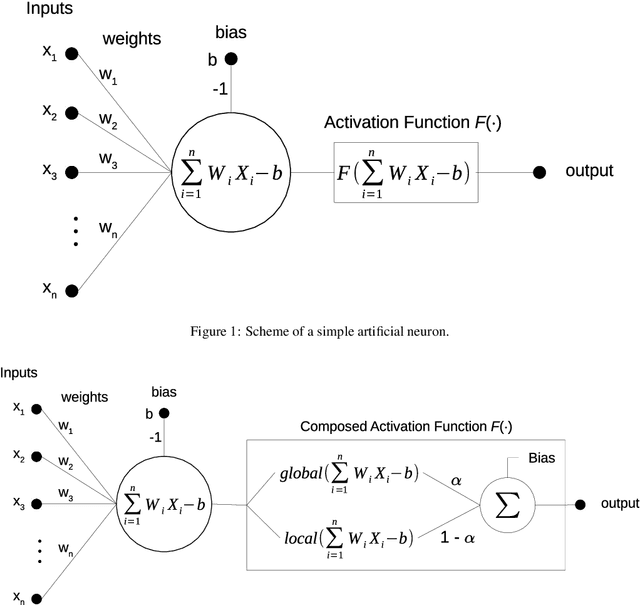
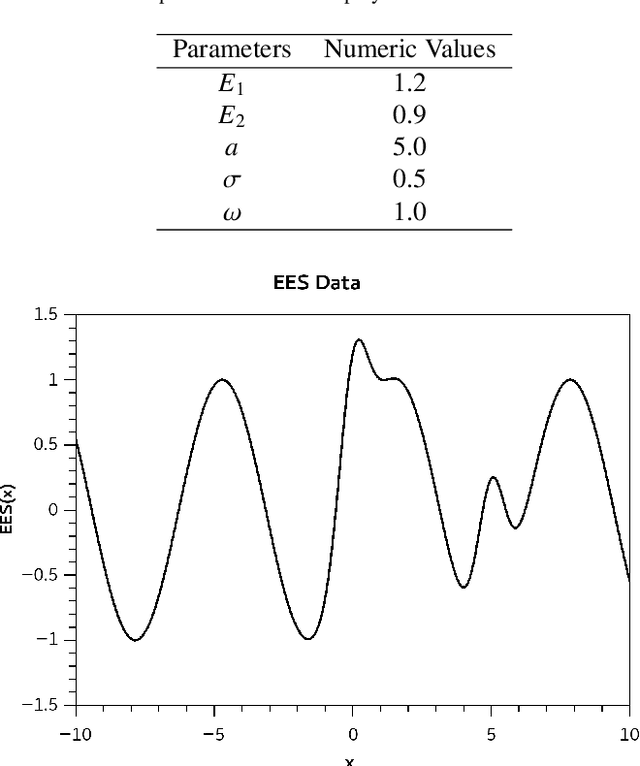
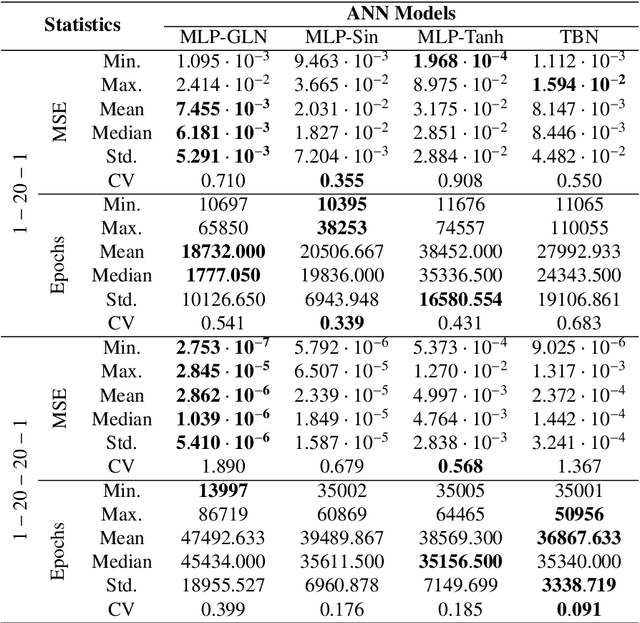
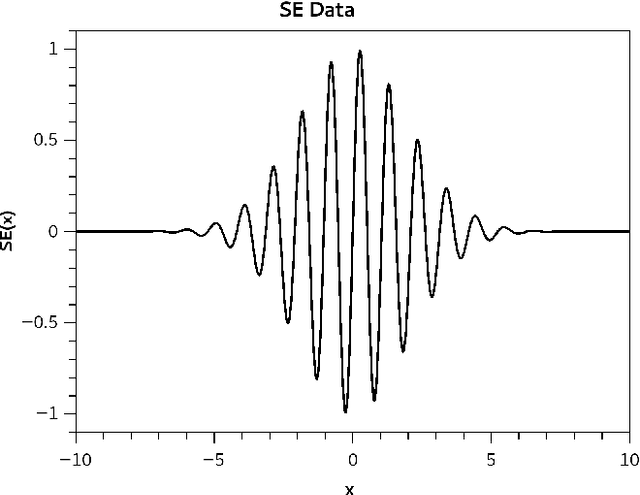
The activation function plays a fundamental role in the artificial neural network learning process. However, there is no obvious choice or procedure to determine the best activation function, which depends on the problem. This study proposes a new artificial neuron, named global-local neuron, with a trainable activation function composed of two components, a global and a local. The global component term used here is relative to a mathematical function to describe a general feature present in all problem domain. The local component is a function that can represent a localized behavior, like a transient or a perturbation. This new neuron can define the importance of each activation function component in the learning phase. Depending on the problem, it results in a purely global, or purely local, or a mixed global and local activation function after the training phase. Here, the trigonometric sine function was employed for the global component and the hyperbolic tangent for the local component. The proposed neuron was tested for problems where the target was a purely global function, or purely local function, or a composition of two global and local functions. Two classes of test problems were investigated, regression problems and differential equations solving. The experimental tests demonstrated the Global-Local Neuron network's superior performance, compared with simple neural networks with sine or hyperbolic tangent activation function, and with a hybrid network that combines these two simple neural networks.