A New Artificial Neuron Proposal with Trainable Simultaneous Local and Global Activation Function
Paper and Code
Jan 15, 2021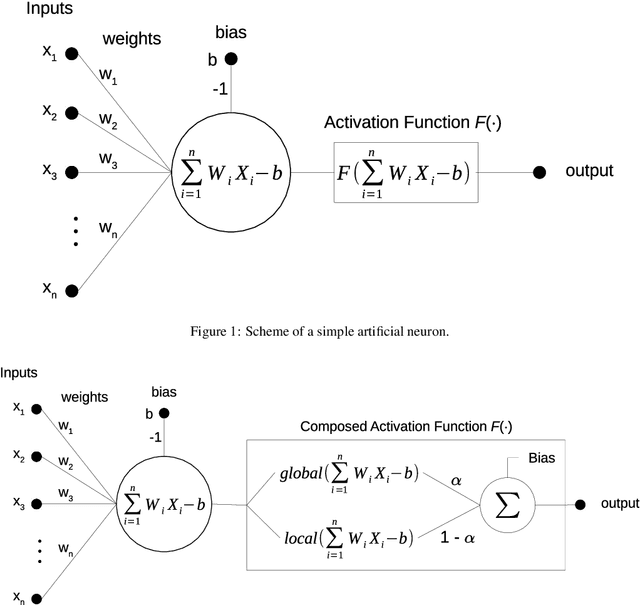
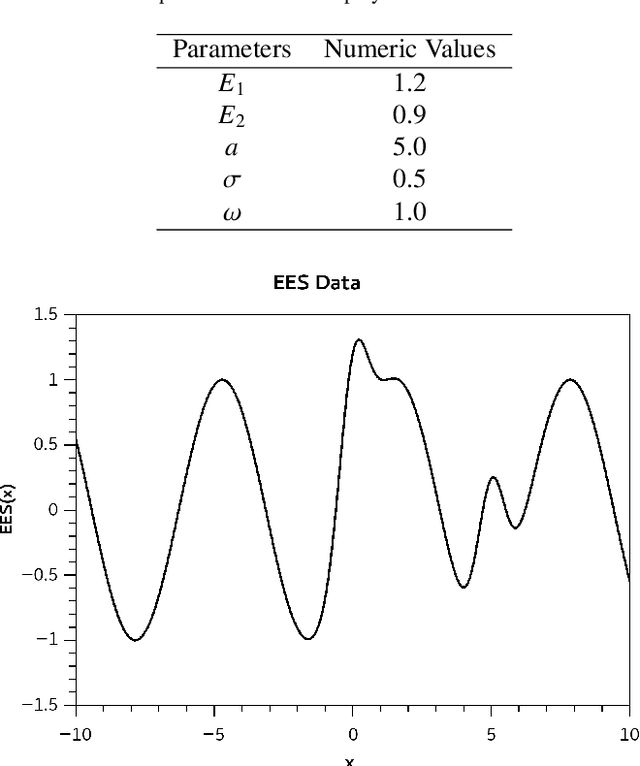
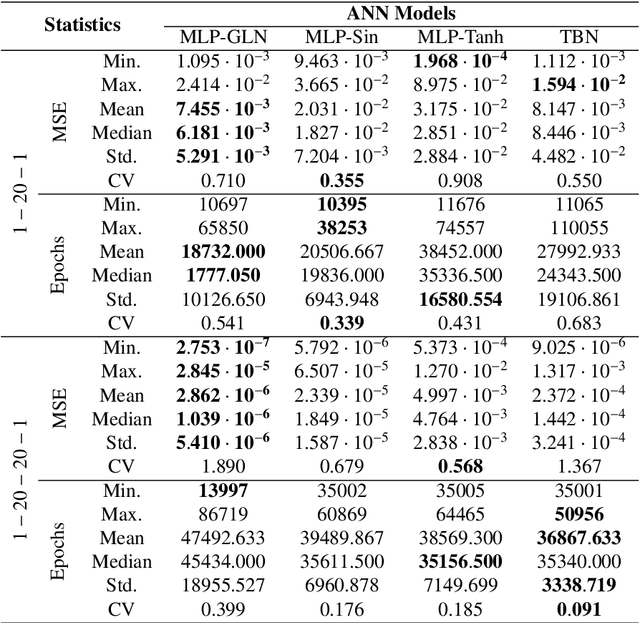
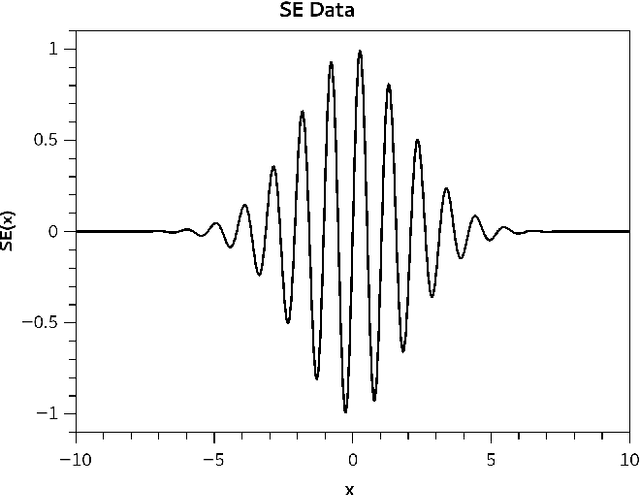
The activation function plays a fundamental role in the artificial neural network learning process. However, there is no obvious choice or procedure to determine the best activation function, which depends on the problem. This study proposes a new artificial neuron, named global-local neuron, with a trainable activation function composed of two components, a global and a local. The global component term used here is relative to a mathematical function to describe a general feature present in all problem domain. The local component is a function that can represent a localized behavior, like a transient or a perturbation. This new neuron can define the importance of each activation function component in the learning phase. Depending on the problem, it results in a purely global, or purely local, or a mixed global and local activation function after the training phase. Here, the trigonometric sine function was employed for the global component and the hyperbolic tangent for the local component. The proposed neuron was tested for problems where the target was a purely global function, or purely local function, or a composition of two global and local functions. Two classes of test problems were investigated, regression problems and differential equations solving. The experimental tests demonstrated the Global-Local Neuron network's superior performance, compared with simple neural networks with sine or hyperbolic tangent activation function, and with a hybrid network that combines these two simple neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge