Encoding Involutory Invariance in Neural Networks

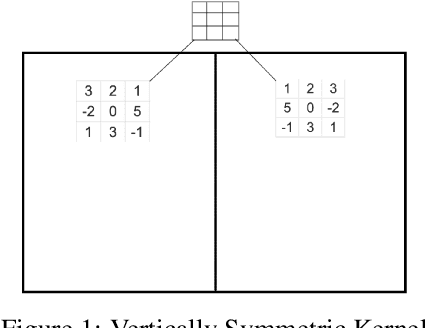
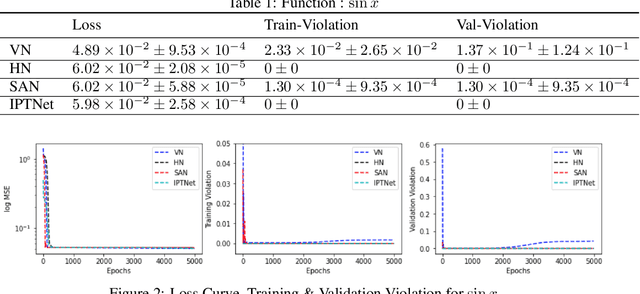
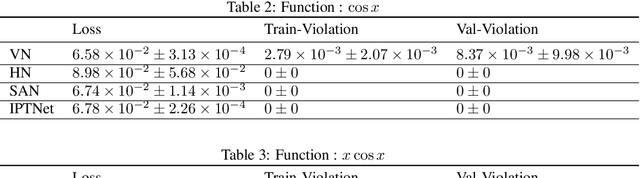
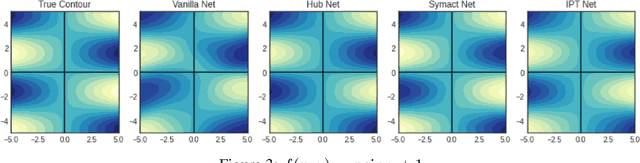
In certain situations, Neural Networks (NN) are trained upon data that obey underlying physical symmetries. However, it is not guaranteed that NNs will obey the underlying symmetry unless embedded in the network structure. In this work, we explore a special kind of symmetry where functions are invariant with respect to involutory linear/affine transformations up to parity $p=\pm 1$. We develop mathematical theorems and propose NN architectures that ensure invariance and universal approximation properties. Numerical experiments indicate that the proposed models outperform baseline networks while respecting the imposed symmetry. An adaption of our technique to convolutional NN classification tasks for datasets with inherent horizontal/vertical reflection symmetry has also been proposed.

Fairly Constricted Particle Swarm Optimization

We have adapted the use of exponentially averaged momentum in PSO to multi-objective optimization problems. The algorithm was built on top of SMPSO, a state-of-the-art MOO solver, and we present a novel mathematical analysis of constriction fairness. We extend this analysis to the use of momentum and propose rich alternatives of parameter sets which are theoretically sound. We call our proposed algorithm "Fairly Constricted PSO with Exponentially-Averaged Momentum", FCPSO-em.

A Swarm Variant for the Schrödinger Solver

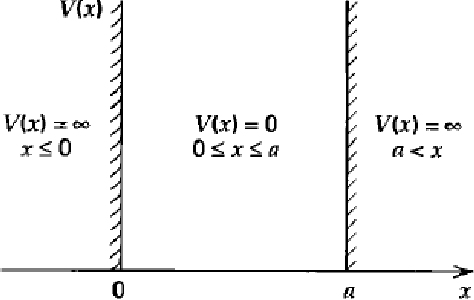
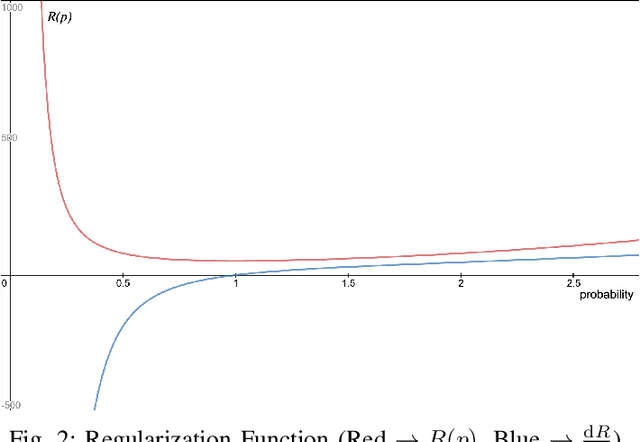
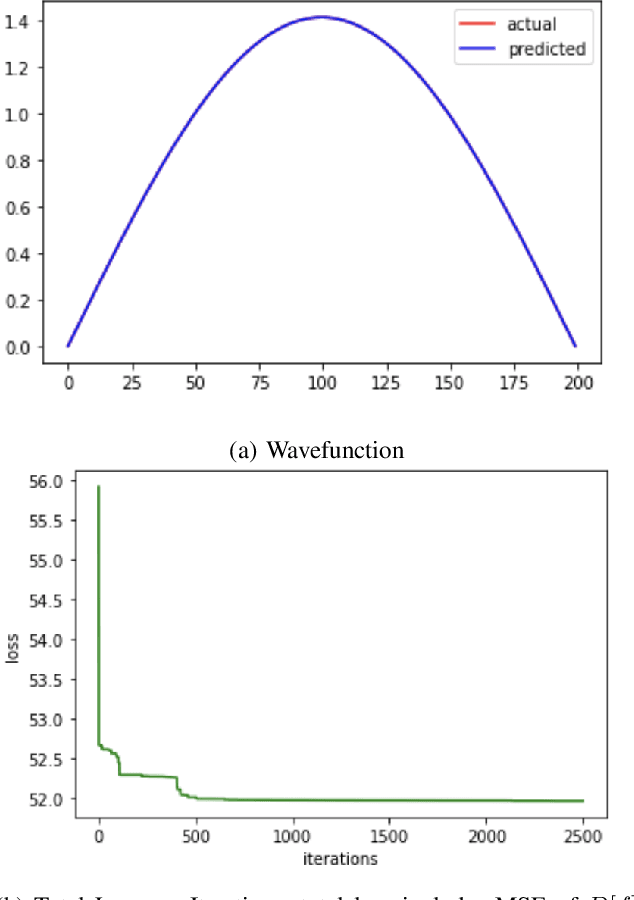
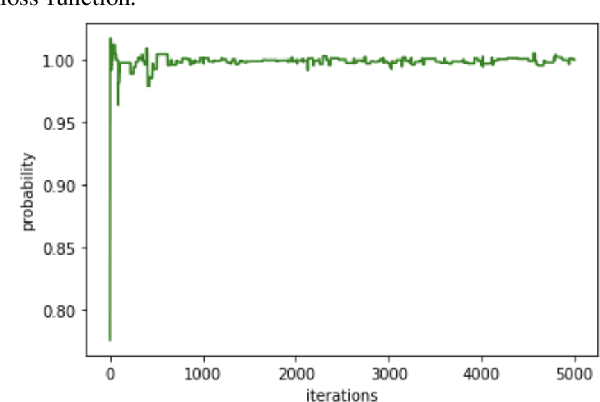
This paper introduces application of the Exponentially Averaged Momentum Particle Swarm Optimization (EM-PSO) as a derivative-free optimizer for Neural Networks. It adopts PSO's major advantages such as search space exploration and higher robustness to local minima compared to gradient-descent optimizers such as Adam. Neural network based solvers endowed with gradient optimization are now being used to approximate solutions to Differential Equations. Here, we demonstrate the novelty of EM-PSO in approximating gradients and leveraging the property in solving the Schr\"odinger equation, for the Particle-in-a-Box problem. We also provide the optimal set of hyper-parameters supported by mathematical proofs, suited for our algorithm.