A Particle-based Sparse Gaussian Process Optimizer

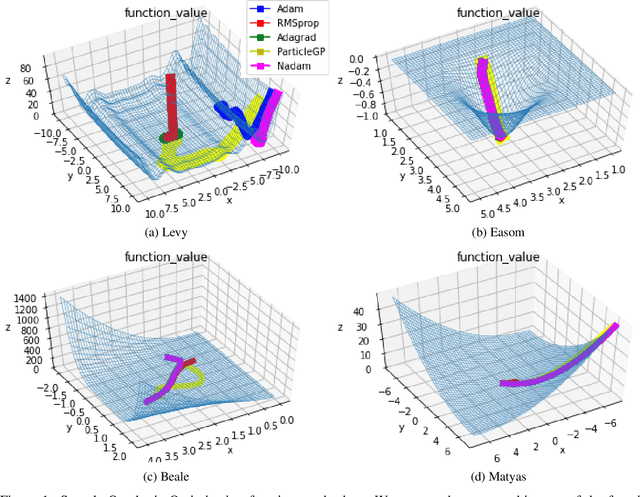
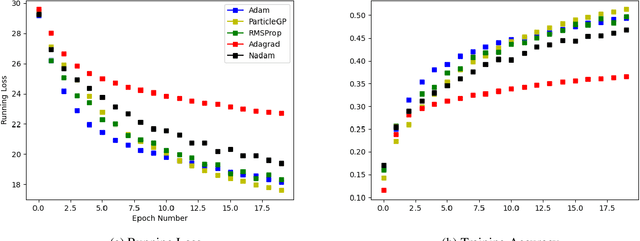
Task learning in neural networks typically requires finding a globally optimal minimizer to a loss function objective. Conventional designs of swarm based optimization methods apply a fixed update rule, with possibly an adaptive step-size for gradient descent based optimization. While these methods gain huge success in solving different optimization problems, there are some cases where these schemes are either inefficient or suffering from local-minimum. We present a new particle-swarm-based framework utilizing Gaussian Process Regression to learn the underlying dynamical process of descent. The biggest advantage of this approach is greater exploration around the current state before deciding a descent direction. Empirical results show our approach can escape from the local minima compare with the widely-used state-of-the-art optimizers when solving non-convex optimization problems. We also test our approach under high-dimensional parameter space case, namely, image classification task.

A Swarm Variant for the Schrödinger Solver

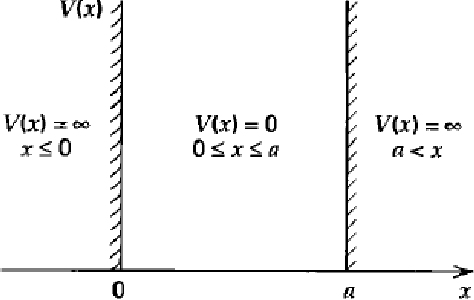
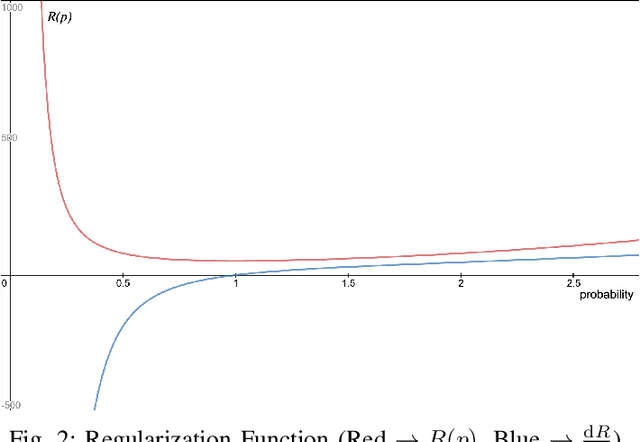
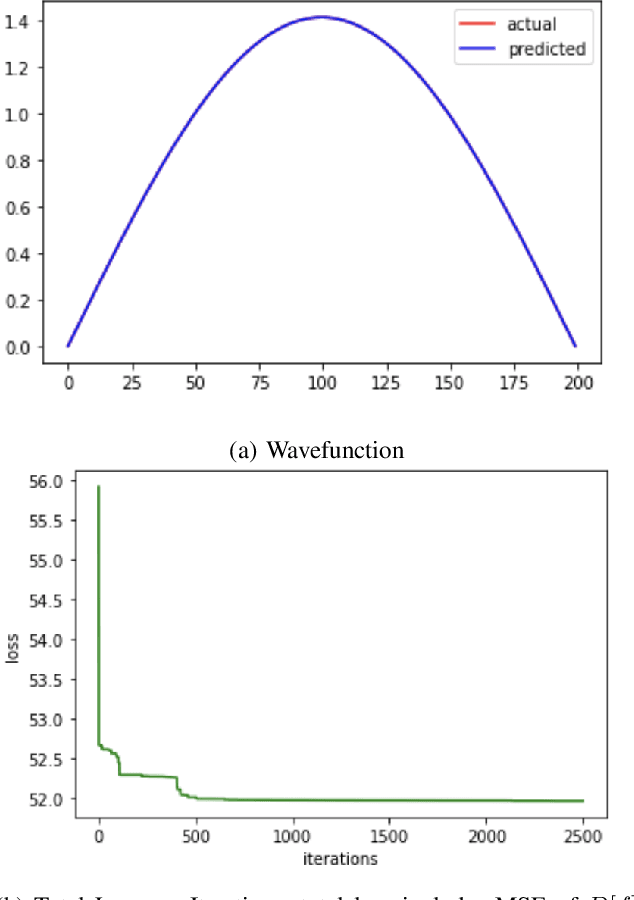
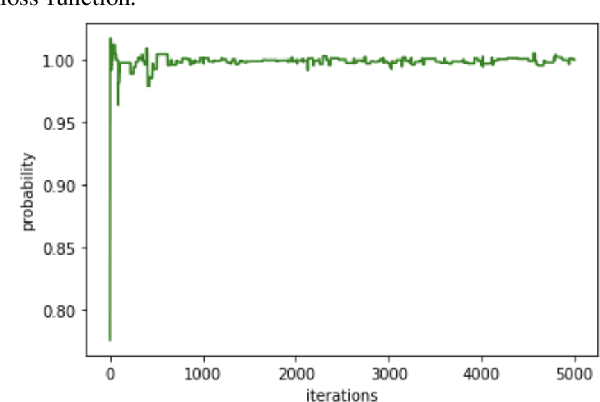
This paper introduces application of the Exponentially Averaged Momentum Particle Swarm Optimization (EM-PSO) as a derivative-free optimizer for Neural Networks. It adopts PSO's major advantages such as search space exploration and higher robustness to local minima compared to gradient-descent optimizers such as Adam. Neural network based solvers endowed with gradient optimization are now being used to approximate solutions to Differential Equations. Here, we demonstrate the novelty of EM-PSO in approximating gradients and leveraging the property in solving the Schr\"odinger equation, for the Particle-in-a-Box problem. We also provide the optimal set of hyper-parameters supported by mathematical proofs, suited for our algorithm.