RcTorch: a PyTorch Reservoir Computing Package with Automated Hyper-Parameter Optimization

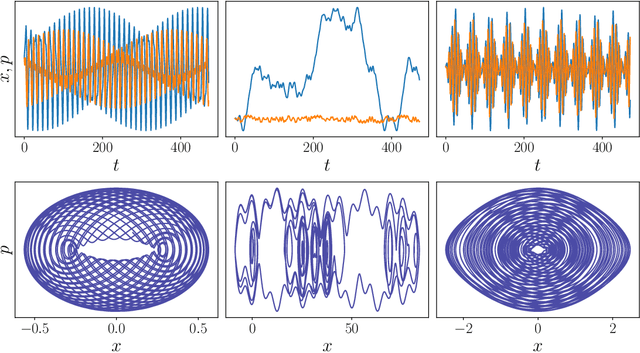
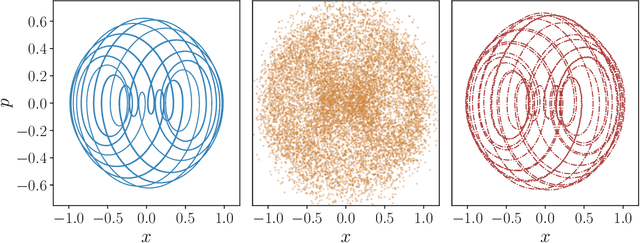
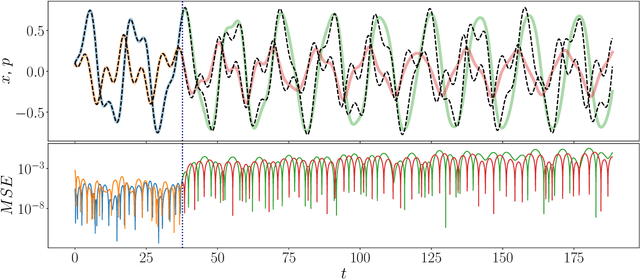
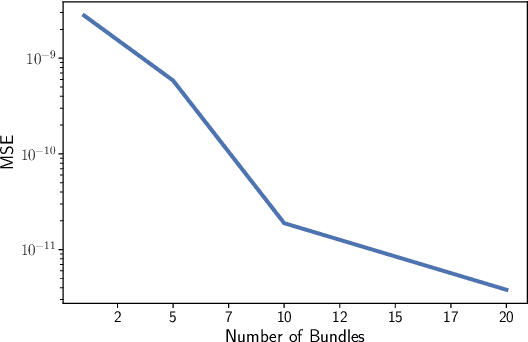
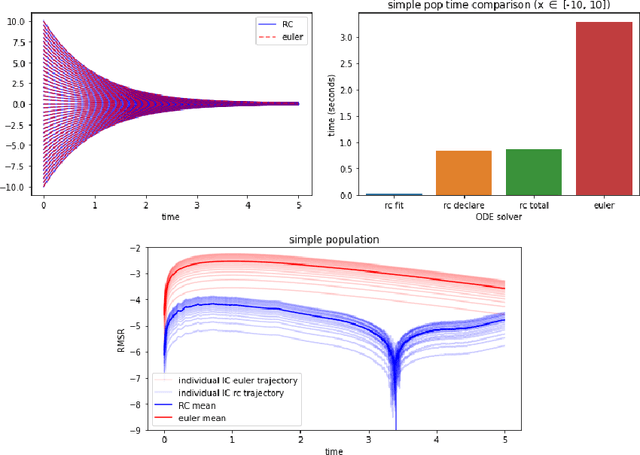
Reservoir computers (RCs) are among the fastest to train of all neural networks, especially when they are compared to other recurrent neural networks. RC has this advantage while still handling sequential data exceptionally well. However, RC adoption has lagged other neural network models because of the model's sensitivity to its hyper-parameters (HPs). A modern unified software package that automatically tunes these parameters is missing from the literature. Manually tuning these numbers is very difficult, and the cost of traditional grid search methods grows exponentially with the number of HPs considered, discouraging the use of the RC and limiting the complexity of the RC models which can be devised. We address these problems by introducing RcTorch, a PyTorch based RC neural network package with automated HP tuning. Herein, we demonstrate the utility of RcTorch by using it to predict the complex dynamics of a driven pendulum being acted upon by varying forces. This work includes coding examples. Example Python Jupyter notebooks can be found on our GitHub repository https://github.com/blindedjoy/RcTorch and documentation can be found at https://rctorch.readthedocs.io/.

One-Shot Transfer Learning of Physics-Informed Neural Networks

Solving differential equations efficiently and accurately sits at the heart of progress in many areas of scientific research, from classical dynamical systems to quantum mechanics. There is a surge of interest in using Physics-Informed Neural Networks (PINNs) to tackle such problems as they provide numerous benefits over traditional numerical approaches. Despite their potential benefits for solving differential equations, transfer learning has been under explored. In this study, we present a general framework for transfer learning PINNs that results in one-shot inference for linear systems of both ordinary and partial differential equations. This means that highly accurate solutions to many unknown differential equations can be obtained instantaneously without retraining an entire network. We demonstrate the efficacy of the proposed deep learning approach by solving several real-world problems, such as first- and second-order linear ordinary equations, the Poisson equation, and the time-dependent Schrodinger complex-value partial differential equation.

Unsupervised Reservoir Computing for Solving Ordinary Differential Equations

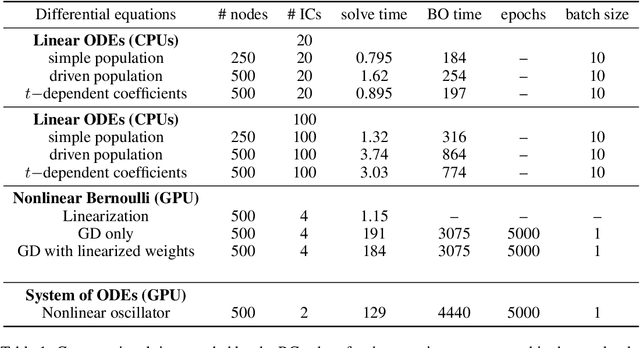
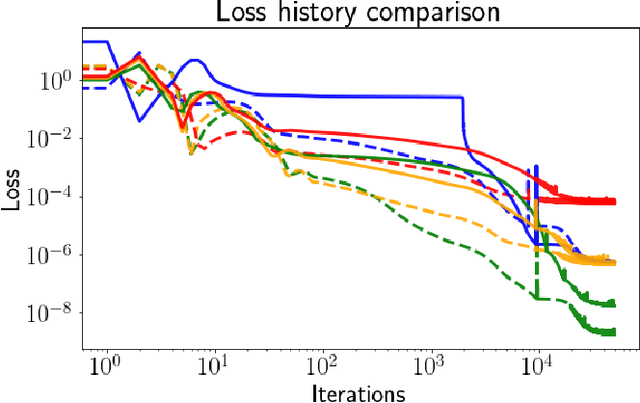
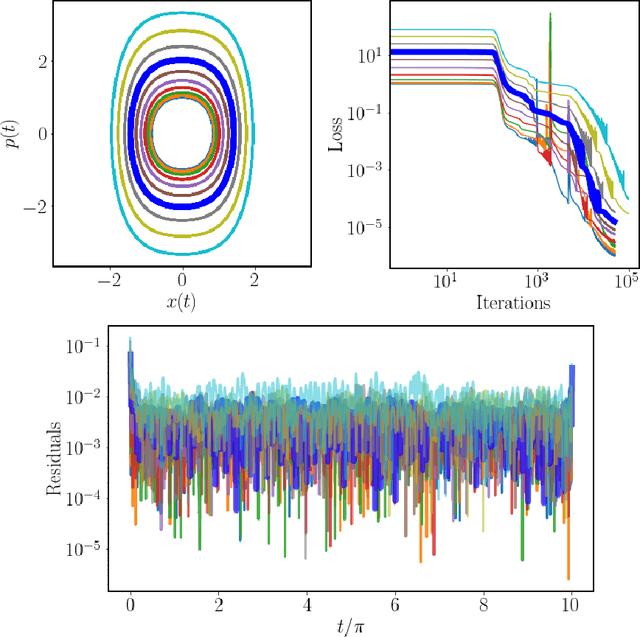
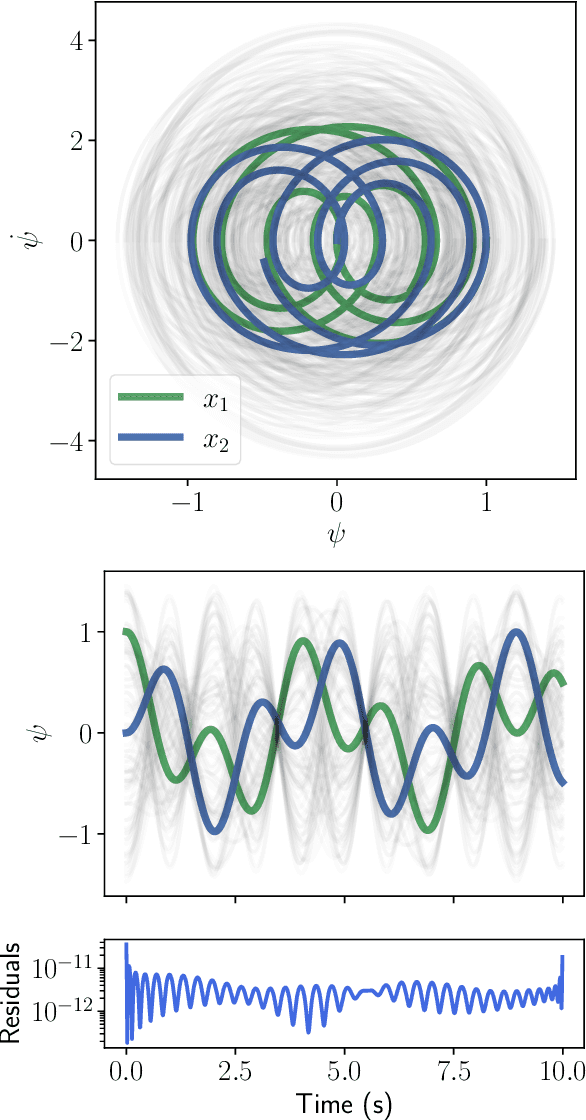
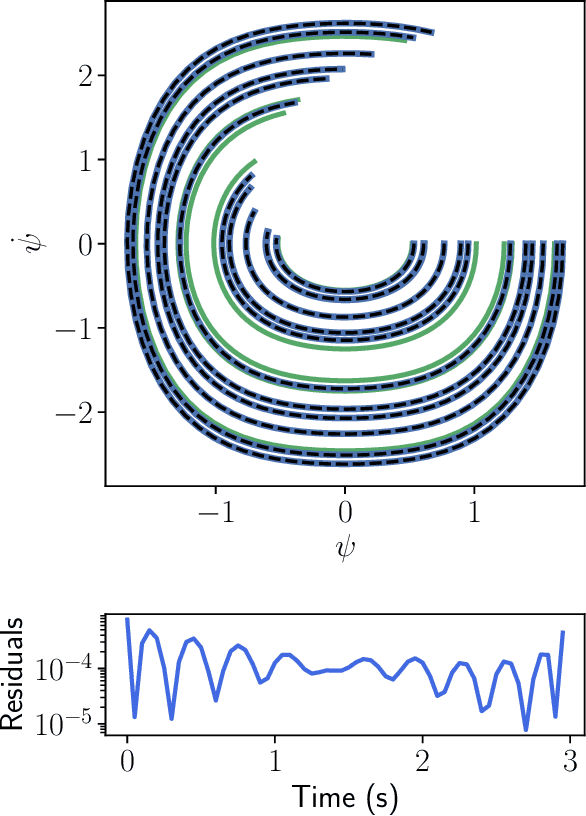
There is a wave of interest in using unsupervised neural networks for solving differential equations. The existing methods are based on feed-forward networks, {while} recurrent neural network differential equation solvers have not yet been reported. We introduce an unsupervised reservoir computing (RC), an echo-state recurrent neural network capable of discovering approximate solutions that satisfy ordinary differential equations (ODEs). We suggest an approach to calculate time derivatives of recurrent neural network outputs without using backpropagation. The internal weights of an RC are fixed, while only a linear output layer is trained, yielding efficient training. However, RC performance strongly depends on finding the optimal hyper-parameters, which is a computationally expensive process. We use Bayesian optimization to efficiently discover optimal sets in a high-dimensional hyper-parameter space and numerically show that one set is robust and can be used to solve an ODE for different initial conditions and time ranges. A closed-form formula for the optimal output weights is derived to solve first order linear equations in a backpropagation-free learning process. We extend the RC approach by solving nonlinear system of ODEs using a hybrid optimization method consisting of gradient descent and Bayesian optimization. Evaluation of linear and nonlinear systems of equations demonstrates the efficiency of the RC ODE solver.