One-Shot Transfer Learning of Physics-Informed Neural Networks

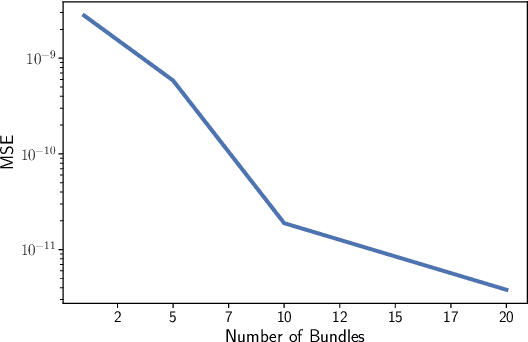
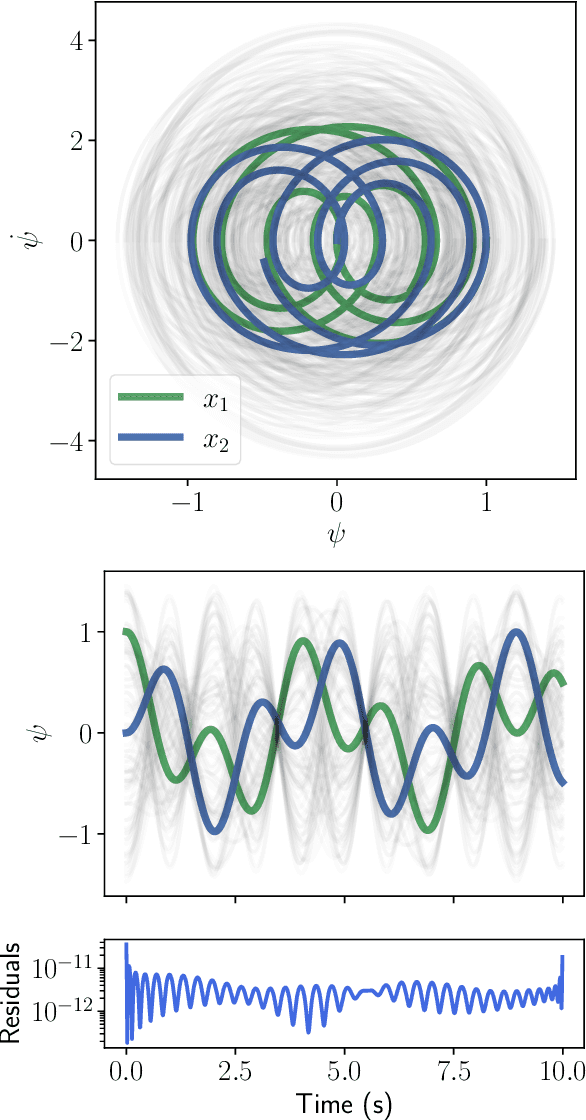
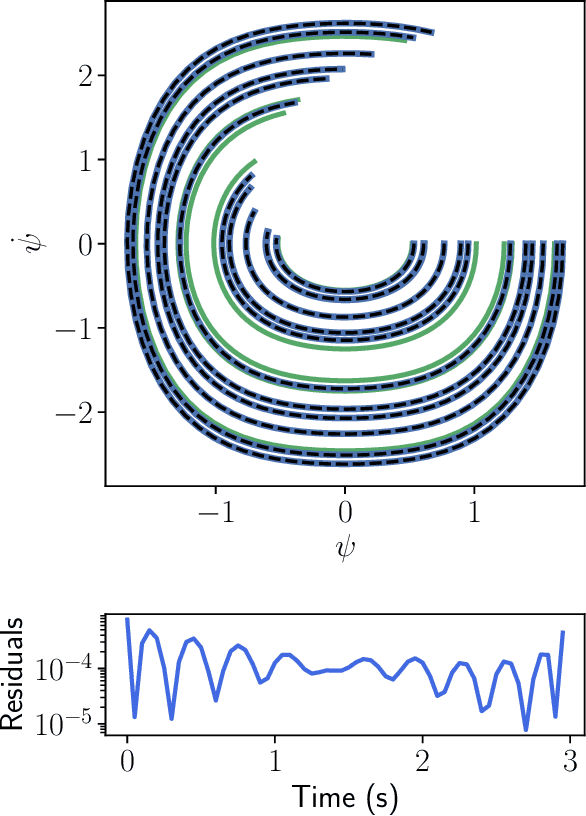
Solving differential equations efficiently and accurately sits at the heart of progress in many areas of scientific research, from classical dynamical systems to quantum mechanics. There is a surge of interest in using Physics-Informed Neural Networks (PINNs) to tackle such problems as they provide numerous benefits over traditional numerical approaches. Despite their potential benefits for solving differential equations, transfer learning has been under explored. In this study, we present a general framework for transfer learning PINNs that results in one-shot inference for linear systems of both ordinary and partial differential equations. This means that highly accurate solutions to many unknown differential equations can be obtained instantaneously without retraining an entire network. We demonstrate the efficacy of the proposed deep learning approach by solving several real-world problems, such as first- and second-order linear ordinary equations, the Poisson equation, and the time-dependent Schrodinger complex-value partial differential equation.

Port-Hamiltonian Neural Networks for Learning Explicit Time-Dependent Dynamical Systems

Accurately learning the temporal behavior of dynamical systems requires models with well-chosen learning biases. Recent innovations embed the Hamiltonian and Lagrangian formalisms into neural networks and demonstrate a significant improvement over other approaches in predicting trajectories of physical systems. These methods generally tackle autonomous systems that depend implicitly on time or systems for which a control signal is known apriori. Despite this success, many real world dynamical systems are non-autonomous, driven by time-dependent forces and experience energy dissipation. In this study, we address the challenge of learning from such non-autonomous systems by embedding the port-Hamiltonian formalism into neural networks, a versatile framework that can capture energy dissipation and time-dependent control forces. We show that the proposed \emph{port-Hamiltonian neural network} can efficiently learn the dynamics of nonlinear physical systems of practical interest and accurately recover the underlying stationary Hamiltonian, time-dependent force, and dissipative coefficient. A promising outcome of our network is its ability to learn and predict chaotic systems such as the Duffing equation, for which the trajectories are typically hard to learn.

Tuning Mixed Input Hyperparameters on the Fly for Efficient Population Based AutoRL

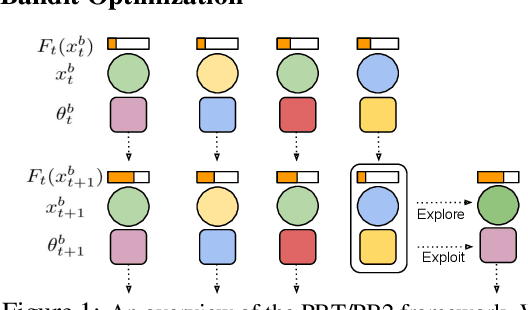
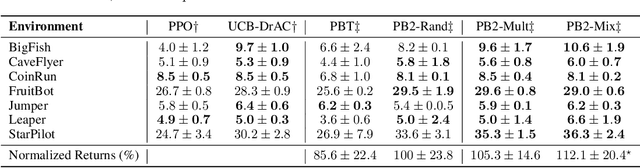
Despite a series of recent successes in reinforcement learning (RL), many RL algorithms remain sensitive to hyperparameters. As such, there has recently been interest in the field of AutoRL, which seeks to automate design decisions to create more general algorithms. Recent work suggests that population based approaches may be effective AutoRL algorithms, by learning hyperparameter schedules on the fly. In particular, the PB2 algorithm is able to achieve strong performance in RL tasks by formulating online hyperparameter optimization as time varying GP-bandit problem, while also providing theoretical guarantees. However, PB2 is only designed to work for continuous hyperparameters, which severely limits its utility in practice. In this paper we introduce a new (provably) efficient hierarchical approach for optimizing both continuous and categorical variables, using a new time-varying bandit algorithm specifically designed for the population based training regime. We evaluate our approach on the challenging Procgen benchmark, where we show that explicitly modelling dependence between data augmentation and other hyperparameters improves generalization.

VIGN: Variational Integrator Graph Networks

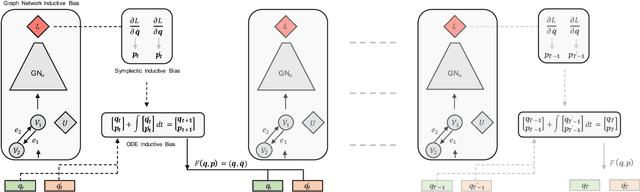
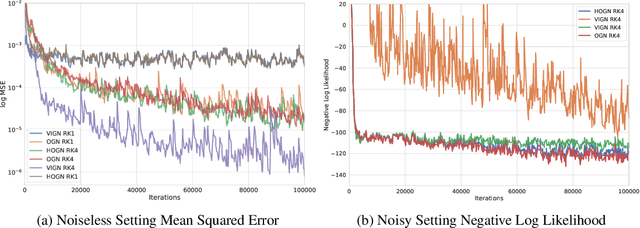
Rich, physically-informed inductive biases play an imperative role in accurately modelling the time dynamics of physical systems. In this paper, we introduce Variational Integrator Graph Networks (VIGNs), the first approach to combine a Variational Integrator (VI) inductive bias with a Graph Network (GN) and demonstrate an order of magnitude improvement in performance, both in terms of data-efficient learning and predictive accuracy, over existing methods. We show that this improvement arises because VIs induce coupled learning of generalized position and momentum updates which can be formulated as a Partitioned Runge-Kutta (PRK) method. We empirically establish that VIGN outperforms numerous methods in learning from existing datasets with noise.

DYNOTEARS: Structure Learning from Time-Series Data

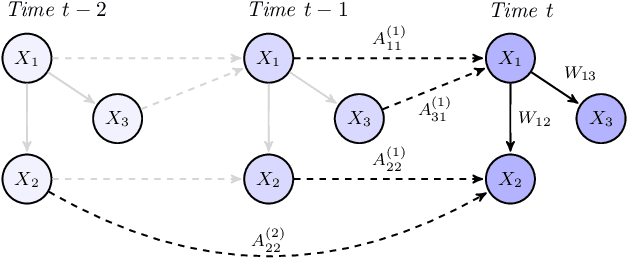
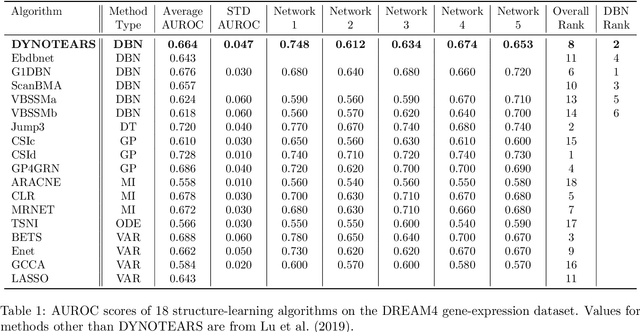
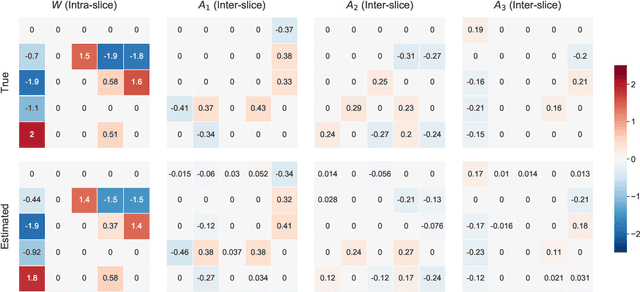
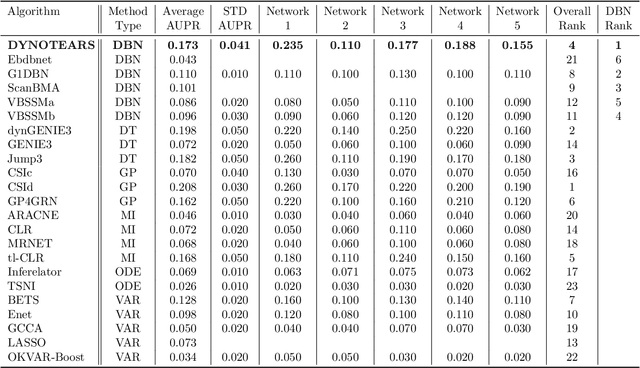
In this paper, we revisit the structure learning problem for dynamic Bayesian networks and propose a method that simultaneously estimates contemporaneous (intra-slice) and time-lagged (inter-slice) relationships between variables in a time-series. Our approach is score-based, and revolves around minimizing a penalized loss subject to an acyclicity constraint. To solve this problem, we leverage a recent algebraic result characterizing the acyclicity constraint as a smooth equality constraint. The resulting algorithm, which we call DYNOTEARS, outperforms other methods on simulated data, especially in high-dimensions as the number of variables increases. We also apply this algorithm on real datasets from two different domains, finance and molecular biology, and analyze the resulting output. Compared to state-of-the-art methods for learning dynamic Bayesian networks, our method is both scalable and accurate on real data. The simple formulation, and competitive performance of our method make it suitable for a variety of problems where one seeks to learn connections between variables across time.