DYNOTEARS: Structure Learning from Time-Series Data

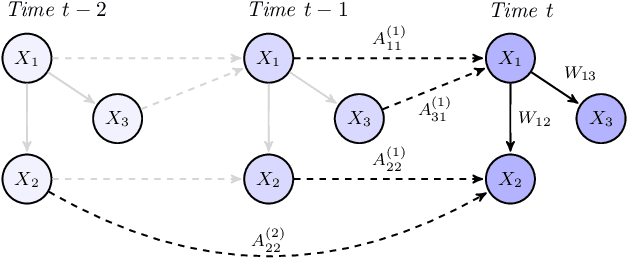
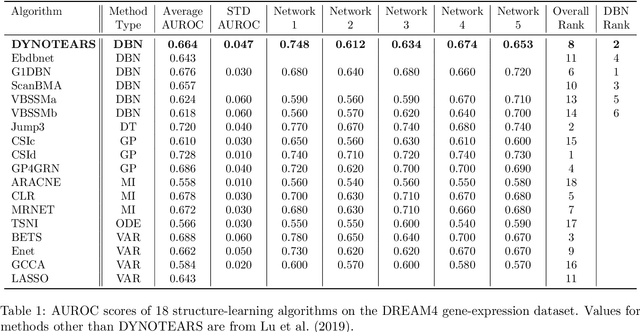
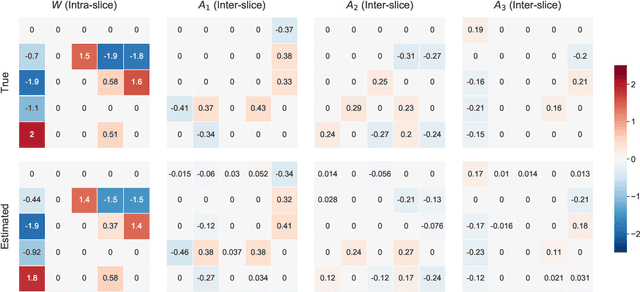
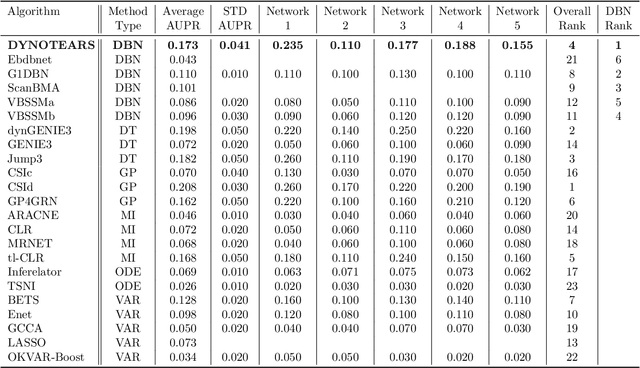
In this paper, we revisit the structure learning problem for dynamic Bayesian networks and propose a method that simultaneously estimates contemporaneous (intra-slice) and time-lagged (inter-slice) relationships between variables in a time-series. Our approach is score-based, and revolves around minimizing a penalized loss subject to an acyclicity constraint. To solve this problem, we leverage a recent algebraic result characterizing the acyclicity constraint as a smooth equality constraint. The resulting algorithm, which we call DYNOTEARS, outperforms other methods on simulated data, especially in high-dimensions as the number of variables increases. We also apply this algorithm on real datasets from two different domains, finance and molecular biology, and analyze the resulting output. Compared to state-of-the-art methods for learning dynamic Bayesian networks, our method is both scalable and accurate on real data. The simple formulation, and competitive performance of our method make it suitable for a variety of problems where one seeks to learn connections between variables across time.

Clusters in Explanation Space: Inferring disease subtypes from model explanations

Identification of disease subtypes and corresponding biomarkers can substantially improve clinical diagnosis and treatment selection. Discovering these subtypes in noisy, high dimensional biomedical data is often impossible for humans and challenging for machines. We introduce a new approach to facilitate the discovery of disease subtypes: Instead of analyzing the original data, we train a diagnostic classifier (healthy vs. diseased) and extract instance-wise explanations for the classifier's decisions. The distribution of instances in the explanation space of our diagnostic classifier amplifies the different reasons for belonging to the same class - resulting in a representation that is uniquely useful for discovering latent subtypes. We compare our ability to recover subtypes via cluster analysis on model explanations to classical cluster analysis on the original data. In multiple datasets with known ground-truth subclasses, most compellingly on UK Biobank brain imaging data and transcriptome data from the Cancer Genome Atlas, we show that cluster analysis on model explanations substantially outperforms the classical approach. While we believe clustering in explanation space to be particularly valuable for inferring disease subtypes, the method is more general and applicable to any kind of sub-type identification.

EMAP: Explanation by Minimal Adversarial Perturbation

Modern instance-based model-agnostic explanation methods (LIME, SHAP, L2X) are of great use in data-heavy industries for model diagnostics, and for end-user explanations. These methods generally return either a weighting or subset of input features as an explanation of the classification of an instance. An alternative literature argues instead that counterfactual instances provide a more useable characterisation of a black box classifier's decisions. We present EMAP, a neural network based approach which returns as Explanation the Minimal Adversarial Perturbation to an instance required to cause the underlying black box model to missclassify. We show that this approach combines the two paradigms, recovering the output of feature-weighting methods in continuous feature spaces, whilst also indicating the direction in which the nearest counterfactuals can be found. Our method also provides an implicit confidence estimate in its own explanations, adding a clarity to model diagnostics other methods lack. Additionally, EMAP improves upon the speed of sampling-based methods such as LIME by an order of magnitude, allowing for model explanations in time-critical applications, or at the dataset level, where sampling-based methods are infeasible. We extend our approach to categorical features using a partitioned Gumbel layer, and demonstrate its efficacy on several standard datasets.

Auditing and Achieving Intersectional Fairness in Classification Problems

Machine learning algorithms are extensively used to make increasingly more consequential decisions, so that achieving optimal predictive performance can no longer be the only focus. This paper explores intersectional fairness, that is fairness when intersections of multiple sensitive attributes -- such as race, age, nationality, etc. -- are considered. Previous research has mainly been focusing on fairness with respect to a single sensitive attribute, with intersectional fairness being comparatively less studied despite its critical importance for modern machine learning applications. We introduce intersectional fairness metrics by extending prior work, and provide different methodologies to audit discrimination in a given dataset or model outputs. Secondly, we develop novel post-processing techniques to mitigate any detected bias in a classification model. Our proposed methodology does not rely on any assumptions regarding the underlying model and aims at guaranteeing fairness while preserving good predictive performance. Finally, we give guidance on a practical implementation, showing how the proposed methods perform on a real-world dataset.

Input-Output Non-Linear Dynamical Systems applied to Physiological Condition Monitoring

We present a non-linear dynamical system for modelling the effect of drug infusions on the vital signs of patients admitted in Intensive Care Units (ICUs). More specifically we are interested in modelling the effect of a widely used anaesthetic drug (Propofol) on a patient's monitored depth of anaesthesia and haemodynamics. We compare our approach with one from the Pharmacokinetics/Pharmacodynamics (PK/PD) literature and show that we can provide significant improvements in performance without requiring the incorporation of expert physiological knowledge in our system.

Discriminative Switching Linear Dynamical Systems applied to Physiological Condition Monitoring

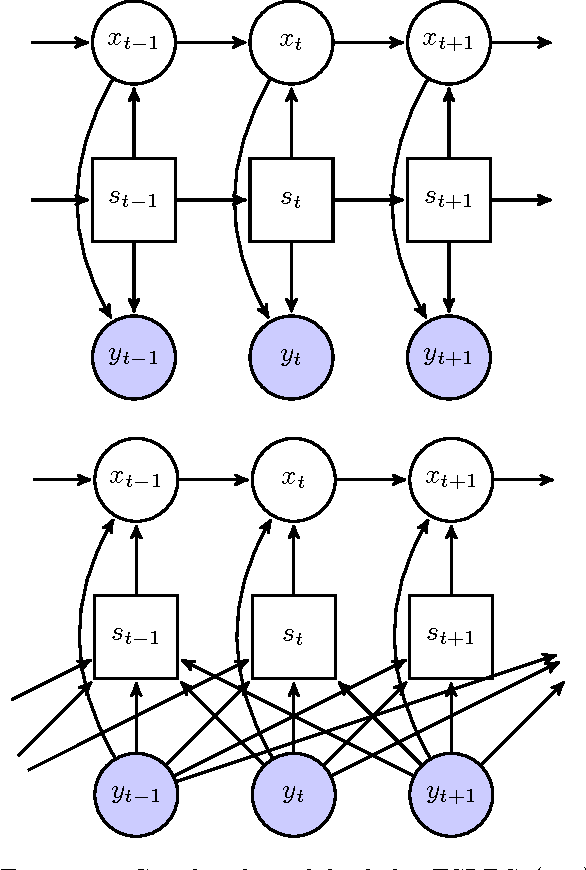
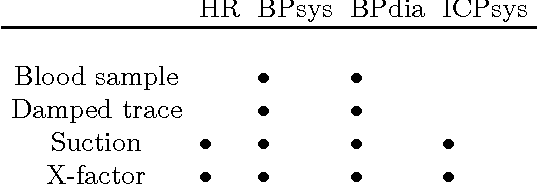
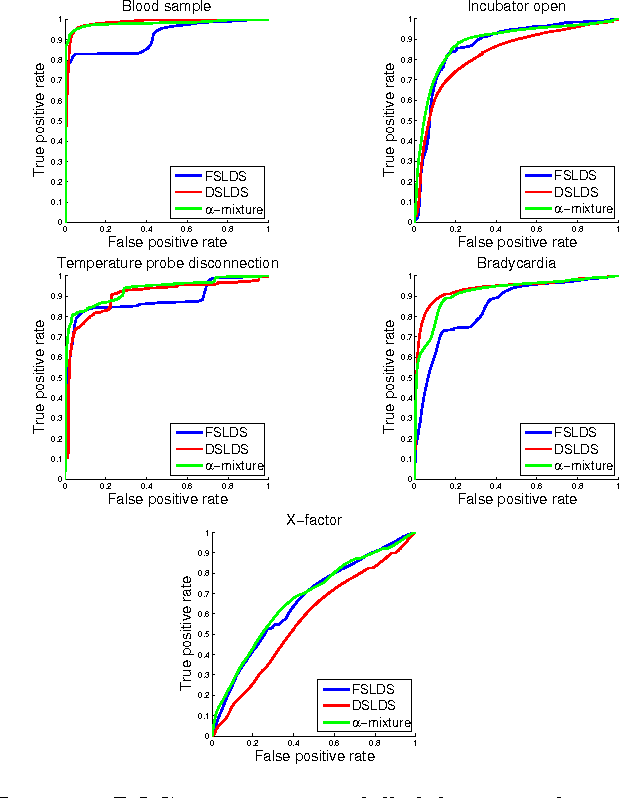
We present a Discriminative Switching Linear Dynamical System (DSLDS) applied to patient monitoring in Intensive Care Units (ICUs). Our approach is based on identifying the state-of-health of a patient given their observed vital signs using a discriminative classifier, and then inferring their underlying physiological values conditioned on this status. The work builds on the Factorial Switching Linear Dynamical System (FSLDS) (Quinn et al., 2009) which has been previously used in a similar setting. The FSLDS is a generative model, whereas the DSLDS is a discriminative model. We demonstrate on two real-world datasets that the DSLDS is able to outperform the FSLDS in most cases of interest, and that an $\alpha$-mixture of the two models achieves higher performance than either of the two models separately.