Bryon Aragam
Towards Interpretable Deep Generative Models via Causal Representation Learning
Apr 15, 2025Abstract:Recent developments in generative artificial intelligence (AI) rely on machine learning techniques such as deep learning and generative modeling to achieve state-of-the-art performance across wide-ranging domains. These methods' surprising performance is due in part to their ability to learn implicit "representations'' of complex, multi-modal data. Unfortunately, deep neural networks are notoriously black boxes that obscure these representations, making them difficult to interpret or analyze. To resolve these difficulties, one approach is to build new interpretable neural network models from the ground up. This is the goal of the emerging field of causal representation learning (CRL) that uses causality as a vector for building flexible, interpretable, and transferable generative AI. CRL can be seen as a culmination of three intrinsically statistical problems: (i) latent variable models such as factor analysis; (ii) causal graphical models with latent variables; and (iii) nonparametric statistics and deep learning. This paper reviews recent progress in CRL from a statistical perspective, focusing on connections to classical models and statistical and causal identifiablity results. This review also highlights key application areas, implementation strategies, and open statistical questions in CRL.
ScoreFlow: Mastering LLM Agent Workflows via Score-based Preference Optimization
Feb 06, 2025Abstract:Recent research has leveraged large language model multi-agent systems for complex problem-solving while trying to reduce the manual effort required to build them, driving the development of automated agent workflow optimization methods. However, existing methods remain inflexible due to representational limitations, a lack of adaptability, and poor scalability when relying on discrete optimization techniques. We address these challenges with ScoreFlow, a simple yet high-performance framework that leverages efficient gradient-based optimization in a continuous space. ScoreFlow incorporates Score-DPO, a novel variant of the direct preference optimization method that accounts for quantitative feedback. Across six benchmarks spanning question answering, coding, and mathematical reasoning, ScoreFlow achieves an 8.2% improvement over existing baselines. Moreover, it empowers smaller models to outperform larger ones with lower inference costs. Project: https://github.com/Gen-Verse/ScoreFlow
Dimension-independent rates for structured neural density estimation
Nov 22, 2024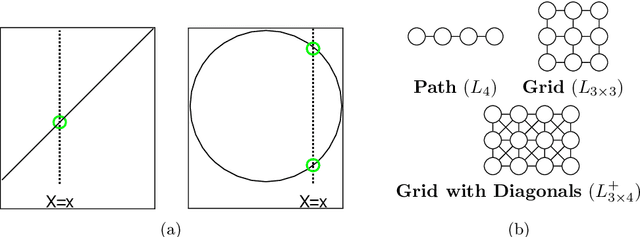



Abstract:We show that deep neural networks achieve dimension-independent rates of convergence for learning structured densities such as those arising in image, audio, video, and text applications. More precisely, we demonstrate that neural networks with a simple $L^2$-minimizing loss achieve a rate of $n^{-1/(4+r)}$ in nonparametric density estimation when the underlying density is Markov to a graph whose maximum clique size is at most $r$, and we provide evidence that in the aforementioned applications, this size is typically constant, i.e., $r=O(1)$. We then establish that the optimal rate in $L^1$ is $n^{-1/(2+r)}$ which, compared to the standard nonparametric rate of $n^{-1/(2+d)}$, reveals that the effective dimension of such problems is the size of the largest clique in the Markov random field. These rates are independent of the data's ambient dimension, making them applicable to realistic models of image, sound, video, and text data. Our results provide a novel justification for deep learning's ability to circumvent the curse of dimensionality, demonstrating dimension-independent convergence rates in these contexts.
Identifying General Mechanism Shifts in Linear Causal Representations
Oct 31, 2024



Abstract:We consider the linear causal representation learning setting where we observe a linear mixing of $d$ unknown latent factors, which follow a linear structural causal model. Recent work has shown that it is possible to recover the latent factors as well as the underlying structural causal model over them, up to permutation and scaling, provided that we have at least $d$ environments, each of which corresponds to perfect interventions on a single latent node (factor). After this powerful result, a key open problem faced by the community has been to relax these conditions: allow for coarser than perfect single-node interventions, and allow for fewer than $d$ of them, since the number of latent factors $d$ could be very large. In this work, we consider precisely such a setting, where we allow a smaller than $d$ number of environments, and also allow for very coarse interventions that can very coarsely \textit{change the entire causal graph over the latent factors}. On the flip side, we relax what we wish to extract to simply the \textit{list of nodes that have shifted between one or more environments}. We provide a surprising identifiability result that it is indeed possible, under some very mild standard assumptions, to identify the set of shifted nodes. Our identifiability proof moreover is a constructive one: we explicitly provide necessary and sufficient conditions for a node to be a shifted node, and show that we can check these conditions given observed data. Our algorithm lends itself very naturally to the sample setting where instead of just interventional distributions, we are provided datasets of samples from each of these distributions. We corroborate our results on both synthetic experiments as well as an interesting psychometric dataset. The code can be found at https://github.com/TianyuCodings/iLCS.
Model-free Estimation of Latent Structure via Multiscale Nonparametric Maximum Likelihood
Oct 29, 2024Abstract:Multivariate distributions often carry latent structures that are difficult to identify and estimate, and which better reflect the data generating mechanism than extrinsic structures exhibited simply by the raw data. In this paper, we propose a model-free approach for estimating such latent structures whenever they are present, without assuming they exist a priori. Given an arbitrary density $p_0$, we construct a multiscale representation of the density and propose data-driven methods for selecting representative models that capture meaningful discrete structure. Our approach uses a nonparametric maximum likelihood estimator to estimate the latent structure at different scales and we further characterize their asymptotic limits. By carrying out such a multiscale analysis, we obtain coarseto-fine structures inherent in the original distribution, which are integrated via a model selection procedure to yield an interpretable discrete representation of it. As an application, we design a clustering algorithm based on the proposed procedure and demonstrate its effectiveness in capturing a wide range of latent structures.
Likelihood-based Differentiable Structure Learning
Oct 08, 2024Abstract:Existing approaches to differentiable structure learning of directed acyclic graphs (DAGs) rely on strong identifiability assumptions in order to guarantee that global minimizers of the acyclicity-constrained optimization problem identifies the true DAG. Moreover, it has been observed empirically that the optimizer may exploit undesirable artifacts in the loss function. We explain and remedy these issues by studying the behavior of differentiable acyclicity-constrained programs under general likelihoods with multiple global minimizers. By carefully regularizing the likelihood, it is possible to identify the sparsest model in the Markov equivalence class, even in the absence of an identifiable parametrization. We first study the Gaussian case in detail, showing how proper regularization of the likelihood defines a score that identifies the sparsest model. Assuming faithfulness, it also recovers the Markov equivalence class. These results are then generalized to general models and likelihoods, where the same claims hold. These theoretical results are validated empirically, showing how this can be done using standard gradient-based optimizers, thus paving the way for differentiable structure learning under general models and losses.
Do LLMs dream of elephants (when told not to)? Latent concept association and associative memory in transformers
Jun 26, 2024



Abstract:Large Language Models (LLMs) have the capacity to store and recall facts. Through experimentation with open-source models, we observe that this ability to retrieve facts can be easily manipulated by changing contexts, even without altering their factual meanings. These findings highlight that LLMs might behave like an associative memory model where certain tokens in the contexts serve as clues to retrieving facts. We mathematically explore this property by studying how transformers, the building blocks of LLMs, can complete such memory tasks. We study a simple latent concept association problem with a one-layer transformer and we show theoretically and empirically that the transformer gathers information using self-attention and uses the value matrix for associative memory.
Greedy equivalence search for nonparametric graphical models
Jun 25, 2024Abstract:One of the hallmark achievements of the theory of graphical models and Bayesian model selection is the celebrated greedy equivalence search (GES) algorithm due to Chickering and Meek. GES is known to consistently estimate the structure of directed acyclic graph (DAG) models in various special cases including Gaussian and discrete models, which are in particular curved exponential families. A general theory that covers general nonparametric DAG models, however, is missing. Here, we establish the consistency of greedy equivalence search for general families of DAG models that satisfy smoothness conditions on the Markov factorization, and hence may not be curved exponential families, or even parametric. The proof leverages recent advances in nonparametric Bayes to construct a test for comparing misspecified DAG models that avoids arguments based on the Laplace approximation. Nonetheless, when the Laplace approximation is valid and a consistent scoring function exists, we recover the classical result. As a result, we obtain a general consistency theorem for GES applied to general DAG models.
On the Origins of Linear Representations in Large Language Models
Mar 06, 2024Abstract:Recent works have argued that high-level semantic concepts are encoded "linearly" in the representation space of large language models. In this work, we study the origins of such linear representations. To that end, we introduce a simple latent variable model to abstract and formalize the concept dynamics of the next token prediction. We use this formalism to show that the next token prediction objective (softmax with cross-entropy) and the implicit bias of gradient descent together promote the linear representation of concepts. Experiments show that linear representations emerge when learning from data matching the latent variable model, confirming that this simple structure already suffices to yield linear representations. We additionally confirm some predictions of the theory using the LLaMA-2 large language model, giving evidence that the simplified model yields generalizable insights.
Learning Interpretable Concepts: Unifying Causal Representation Learning and Foundation Models
Feb 14, 2024Abstract:To build intelligent machine learning systems, there are two broad approaches. One approach is to build inherently interpretable models, as endeavored by the growing field of causal representation learning. The other approach is to build highly-performant foundation models and then invest efforts into understanding how they work. In this work, we relate these two approaches and study how to learn human-interpretable concepts from data. Weaving together ideas from both fields, we formally define a notion of concepts and show that they can be provably recovered from diverse data. Experiments on synthetic data and large language models show the utility of our unified approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge