Dimension-independent rates for structured neural density estimation

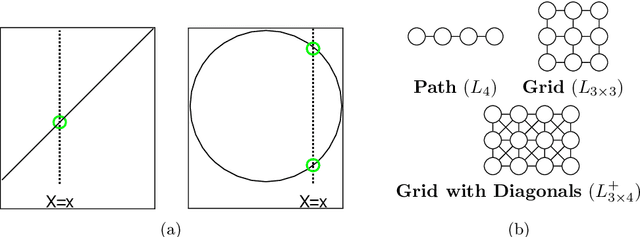
We show that deep neural networks achieve dimension-independent rates of convergence for learning structured densities such as those arising in image, audio, video, and text applications. More precisely, we demonstrate that neural networks with a simple $L^2$-minimizing loss achieve a rate of $n^{-1/(4+r)}$ in nonparametric density estimation when the underlying density is Markov to a graph whose maximum clique size is at most $r$, and we provide evidence that in the aforementioned applications, this size is typically constant, i.e., $r=O(1)$. We then establish that the optimal rate in $L^1$ is $n^{-1/(2+r)}$ which, compared to the standard nonparametric rate of $n^{-1/(2+d)}$, reveals that the effective dimension of such problems is the size of the largest clique in the Markov random field. These rates are independent of the data's ambient dimension, making them applicable to realistic models of image, sound, video, and text data. Our results provide a novel justification for deep learning's ability to circumvent the curse of dimensionality, demonstrating dimension-independent convergence rates in these contexts.

Set Learning for Accurate and Calibrated Models

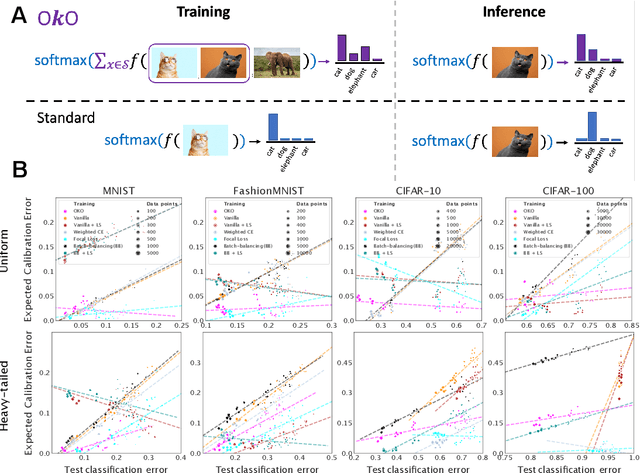
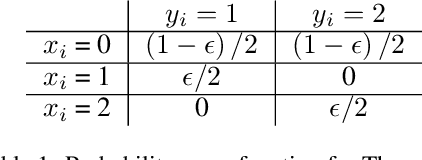
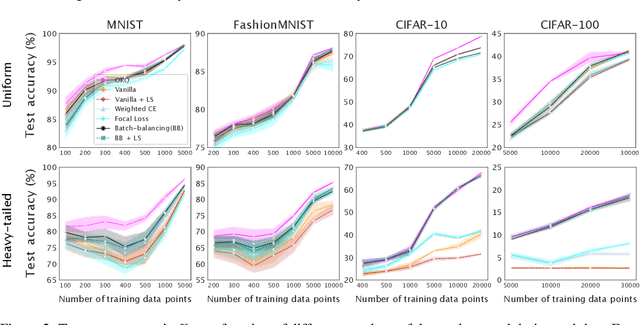
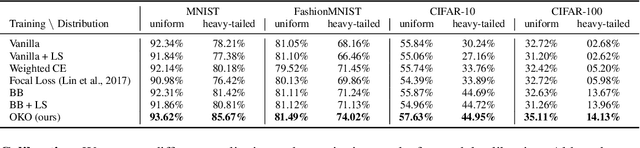
Model overconfidence and poor calibration are common in machine learning and difficult to account for when applying standard empirical risk minimization. In this work, we propose a novel method to alleviate these problems that we call odd-$k$-out learning (OKO), which minimizes the cross-entropy error for sets rather than for single examples. This naturally allows the model to capture correlations across data examples and achieves both better accuracy and calibration, especially in limited training data and class-imbalanced regimes. Perhaps surprisingly, OKO often yields better calibration even when training with hard labels and dropping any additional calibration parameter tuning, such as temperature scaling. We provide theoretical justification, establishing that OKO naturally yields better calibration, and provide extensive experimental analyses that corroborate our theoretical findings. We emphasize that OKO is a general framework that can be easily adapted to many settings and the trained model can be applied to single examples at inference time, without introducing significant run-time overhead or architecture changes.

Improving neural network representations using human similarity judgments

Deep neural networks have reached human-level performance on many computer vision tasks. However, the objectives used to train these networks enforce only that similar images are embedded at similar locations in the representation space, and do not directly constrain the global structure of the resulting space. Here, we explore the impact of supervising this global structure by linearly aligning it with human similarity judgments. We find that a naive approach leads to large changes in local representational structure that harm downstream performance. Thus, we propose a novel method that aligns the global structure of representations while preserving their local structure. This global-local transform considerably improves accuracy across a variety of few-shot learning and anomaly detection tasks. Our results indicate that human visual representations are globally organized in a way that facilitates learning from few examples, and incorporating this global structure into neural network representations improves performance on downstream tasks.

Sample Complexity Using Infinite Multiview Models

Recent works have demonstrated that the convergence rate of a nonparametric density estimator can be greatly improved by using a low-rank estimator when the target density is a convex combination of separable probability densities with Lipschitz continuous marginals, i.e. a multiview model. However, this assumption is very restrictive and it is not clear to what degree these findings can be extended to general pdfs. This work answers this question by introducing a new way of characterizing a pdf's complexity, the non-negative Lipschitz spectrum (NL-spectrum), which, unlike smoothness properties, can be used to characterize virtually any pdf. Finite sample bounds are presented that are dependent on the target density's NL-spectrum. From this dimension-independent rates of convergence are derived that characterize when an NL-spectrum allows for a fast rate of convergence.

Human alignment of neural network representations

Today's computer vision models achieve human or near-human level performance across a wide variety of vision tasks. However, their architectures, data, and learning algorithms differ in numerous ways from those that give rise to human vision. In this paper, we investigate the factors that affect alignment between the representations learned by neural networks and human concept representations. Human representations are inferred from behavioral responses in an odd-one-out triplet task, where humans were presented with three images and had to select the odd-one-out. We find that model scale and architecture have essentially no effect on alignment with human behavioral responses, whereas the training dataset and objective function have a much larger impact. Using a sparse Bayesian model of human conceptual representations, we partition triplets by the concept that distinguishes the two similar images from the odd-one-out, finding that some concepts such as food and animals are well-represented in neural network representations whereas others such as royal or sports-related objects are not. Overall, although models trained on larger, more diverse datasets achieve better alignment with humans than models trained on ImageNet alone, our results indicate that scaling alone is unlikely to be sufficient to train neural networks with conceptual representations that match those used by humans.

Generalized Identifiability Bounds for Mixture Models with Grouped Samples

Recent work has shown that finite mixture models with $m$ components are identifiable, while making no assumptions on the mixture components, so long as one has access to groups of samples of size $2m-1$ which are known to come from the same mixture component. In this work we generalize that result and show that, if every subset of $k$ mixture components of a mixture model are linearly independent, then that mixture model is identifiable with only $(2m-1)/(k-1)$ samples per group. We further show that this value cannot be improved. We prove an analogous result for a stronger form of identifiability known as "determinedness" along with a corresponding lower bound. This independence assumption almost surely holds if mixture components are chosen randomly from a $k$-dimensional space. We describe some implications of our results for multinomial mixture models and topic modeling.

Exposing Outlier Exposure: What Can Be Learned From Few, One, and Zero Outlier Images

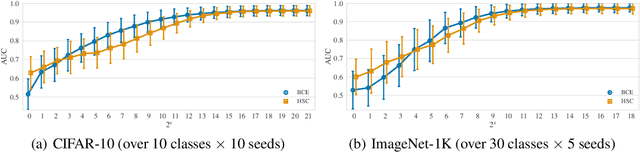
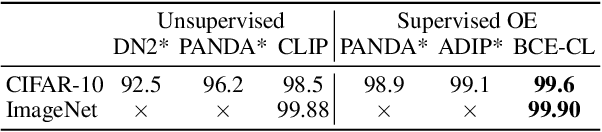
Traditionally anomaly detection (AD) is treated as an unsupervised problem utilizing only normal samples due to the intractability of characterizing everything that looks unlike the normal data. However, it has recently been found that unsupervised image anomaly detection can be drastically improved through the utilization of huge corpora of random images to represent anomalousness; a technique which is known as Outlier Exposure. In this paper we show that specialized AD learning methods seem actually superfluous and huge corpora of data expendable. For a common AD benchmark on ImageNet, standard classifiers and semi-supervised one-class methods trained to discern between normal samples and just a few random natural images are able to outperform the current state of the art in deep AD, and only one useful outlier sample is sufficient to perform competitively. We investigate this phenomenon and reveal that one-class methods are more robust towards the particular choice of training outliers. Furthermore, we find that a simple classifier based on representations from CLIP, a recent foundation model, achieves state-of-the-art results on CIFAR-10 and also outperforms all previous AD methods on ImageNet without any training samples (i.e., in a zero-shot setting).

VICE: Variational Interpretable Concept Embeddings

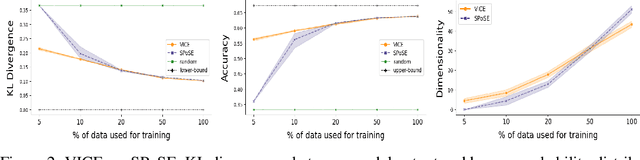
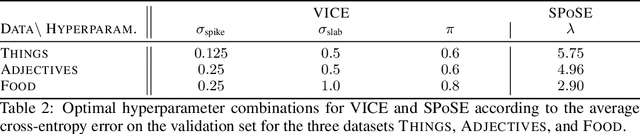
A central goal in the cognitive sciences is the development of computational models of mental representations of object concepts. This paper introduces Variational Interpretable Concept Embeddings (VICE), an approximate Bayesian method for learning interpretable object concept embeddings from human behavior in an odd-one-out triplet task. We use variational inference to obtain a sparse, non-negative solution with uncertainty estimates about each embedding value. We exploit these estimates to select the dimensions that explain the data automatically. We introduce a PAC learning bound for VICE that can be used to estimate generalization performance or determine a sufficient sample size for different experimental designs. VICE rivals or outperforms its predecessor, SPoSE, at predicting human behavior in the odd-one-out triplet task. Furthermore, VICE object representations are substantially more reproducible and consistent across random initializations.

Beyond Smoothness: Incorporating Low-Rank Analysis into Nonparametric Density Estimation

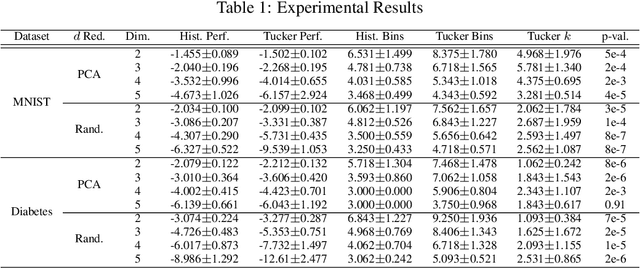
The construction and theoretical analysis of the most popular universally consistent nonparametric density estimators hinge on one functional property: smoothness. In this paper we investigate the theoretical implications of incorporating a multi-view latent variable model, a type of low-rank model, into nonparametric density estimation. To do this we perform extensive analysis on histogram-style estimators that integrate a multi-view model. Our analysis culminates in showing that there exists a universally consistent histogram-style estimator that converges to any multi-view model with a finite number of Lipschitz continuous components at a rate of $\widetilde{O}(1/\sqrt[3]{n})$ in $L^1$ error. In contrast, the standard histogram estimator can converge at a rate slower than $1/\sqrt[d]{n}$ on the same class of densities. We also introduce a new nonparametric latent variable model based on the Tucker decomposition. A rudimentary implementation of our estimators experimentally demonstrates a considerable performance improvement over the standard histogram estimator. We also provide a thorough analysis of the sample complexity of our Tucker decomposition-based model and a variety of other results. Thus, our paper provides solid theoretical foundations for extending low-rank techniques to the nonparametric setting

Learning Interpretable Concept Groups in CNNs

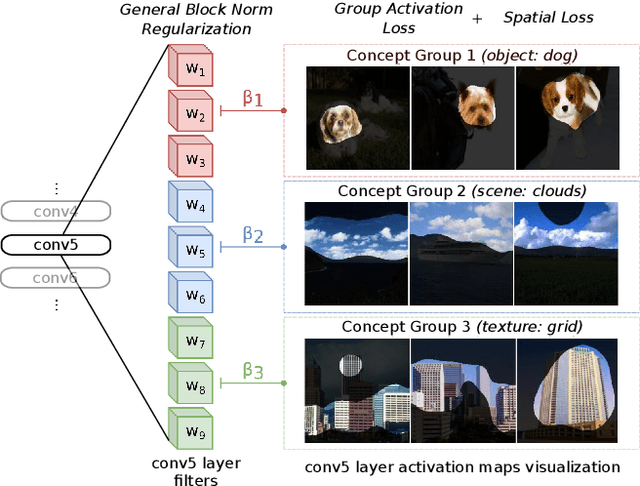
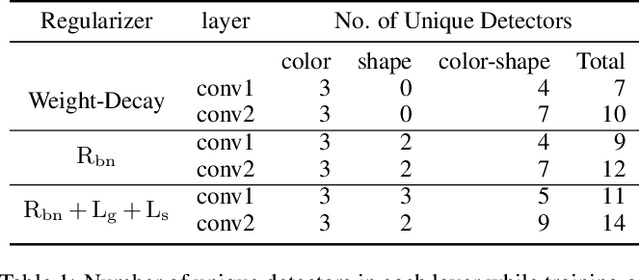
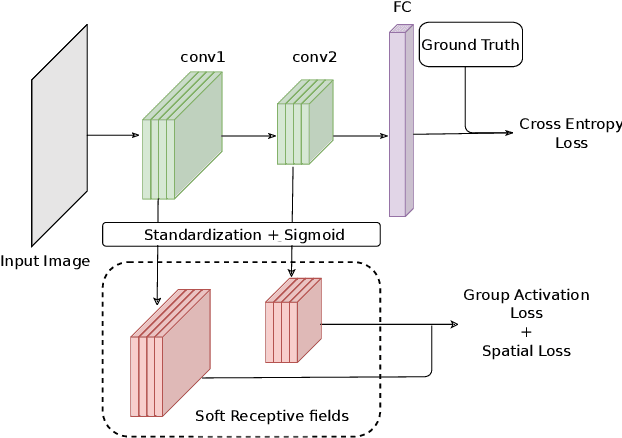
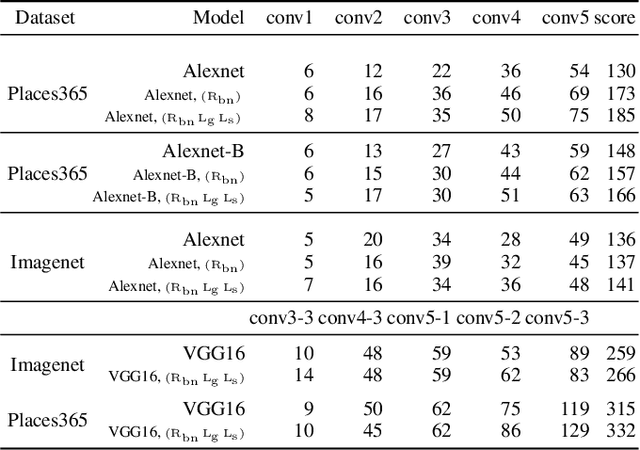
We propose a novel training methodology -- Concept Group Learning (CGL) -- that encourages training of interpretable CNN filters by partitioning filters in each layer into concept groups, each of which is trained to learn a single visual concept. We achieve this through a novel regularization strategy that forces filters in the same group to be active in similar image regions for a given layer. We additionally use a regularizer to encourage a sparse weighting of the concept groups in each layer so that a few concept groups can have greater importance than others. We quantitatively evaluate CGL's model interpretability using standard interpretability evaluation techniques and find that our method increases interpretability scores in most cases. Qualitatively we compare the image regions that are most active under filters learned using CGL versus filters learned without CGL and find that CGL activation regions more strongly concentrate around semantically relevant features.