Explainable Neural Networks with Guarantees: A Sparse Estimation Approach

Balancing predictive power and interpretability has long been a challenging research area, particularly in powerful yet complex models like neural networks, where nonlinearity obstructs direct interpretation. This paper introduces a novel approach to constructing an explainable neural network that harmonizes predictiveness and explainability. Our model, termed SparXnet, is designed as a linear combination of a sparse set of jointly learned features, each derived from a different trainable function applied to a single 1-dimensional input feature. Leveraging the ability to learn arbitrarily complex relationships, our neural network architecture enables automatic selection of a sparse set of important features, with the final prediction being a linear combination of rescaled versions of these features. We demonstrate the ability to select significant features while maintaining comparable predictive performance and direct interpretability through extensive experiments on synthetic and real-world datasets. We also provide theoretical analysis on the generalization bounds of our framework, which is favorably linear in the number of selected features and only logarithmic in the number of input features. We further lift any dependence of sample complexity on the number of parameters or the architectural details under very mild conditions. Our research paves the way for further research on sparse and explainable neural networks with guarantee.

Generalization Analysis for Deep Contrastive Representation Learning

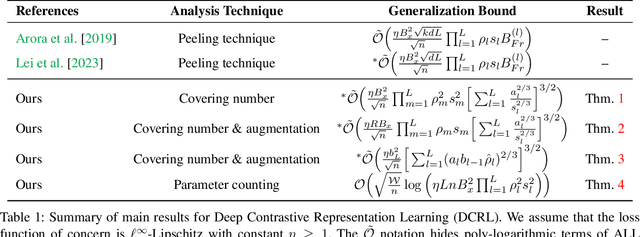
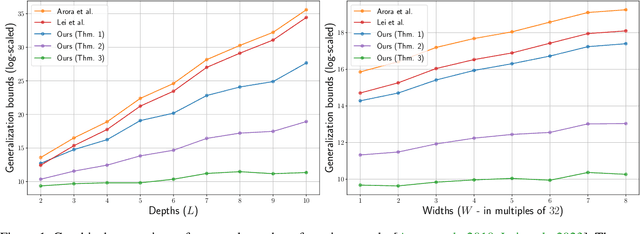
In this paper, we present generalization bounds for the unsupervised risk in the Deep Contrastive Representation Learning framework, which employs deep neural networks as representation functions. We approach this problem from two angles. On the one hand, we derive a parameter-counting bound that scales with the overall size of the neural networks. On the other hand, we provide a norm-based bound that scales with the norms of neural networks' weight matrices. Ignoring logarithmic factors, the bounds are independent of $k$, the size of the tuples provided for contrastive learning. To the best of our knowledge, this property is only shared by one other work, which employed a different proof strategy and suffers from very strong exponential dependence on the depth of the network which is due to a use of the peeling technique. Our results circumvent this by leveraging powerful results on covering numbers with respect to uniform norms over samples. In addition, we utilize loss augmentation techniques to further reduce the dependency on matrix norms and the implicit dependence on network depth. In fact, our techniques allow us to produce many bounds for the contrastive learning setting with similar architectural dependencies as in the study of the sample complexity of ordinary loss functions, thereby bridging the gap between the learning theories of contrastive learning and DNNs.

Interpretable Tensor Fusion

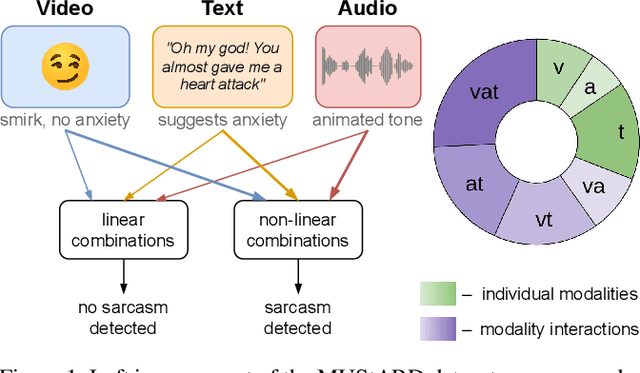
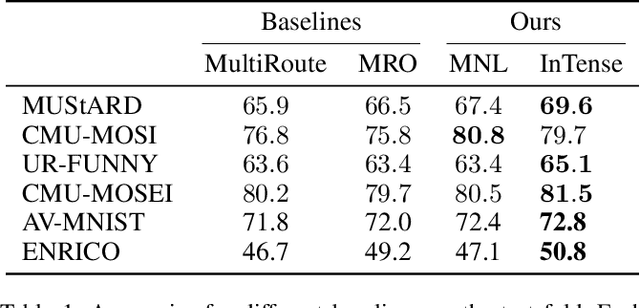
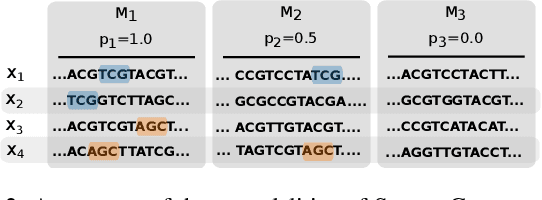
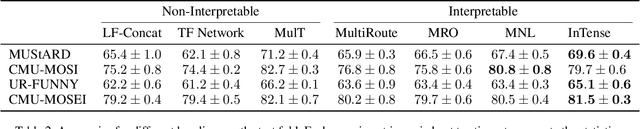
Conventional machine learning methods are predominantly designed to predict outcomes based on a single data type. However, practical applications may encompass data of diverse types, such as text, images, and audio. We introduce interpretable tensor fusion (InTense), a multimodal learning method for training neural networks to simultaneously learn multimodal data representations and their interpretable fusion. InTense can separately capture both linear combinations and multiplicative interactions of diverse data types, thereby disentangling higher-order interactions from the individual effects of each modality. InTense provides interpretability out of the box by assigning relevance scores to modalities and their associations. The approach is theoretically grounded and yields meaningful relevance scores on multiple synthetic and real-world datasets. Experiments on six real-world datasets show that InTense outperforms existing state-of-the-art multimodal interpretable approaches in terms of accuracy and interpretability.

Generalization Bounds for Inductive Matrix Completion in Low-noise Settings

We study inductive matrix completion (matrix completion with side information) under an i.i.d. subgaussian noise assumption at a low noise regime, with uniform sampling of the entries. We obtain for the first time generalization bounds with the following three properties: (1) they scale like the standard deviation of the noise and in particular approach zero in the exact recovery case; (2) even in the presence of noise, they converge to zero when the sample size approaches infinity; and (3) for a fixed dimension of the side information, they only have a logarithmic dependence on the size of the matrix. Differently from many works in approximate recovery, we present results both for bounded Lipschitz losses and for the absolute loss, with the latter relying on Talagrand-type inequalities. The proofs create a bridge between two approaches to the theoretical analysis of matrix completion, since they consist in a combination of techniques from both the exact recovery literature and the approximate recovery literature.

Beyond Smoothness: Incorporating Low-Rank Analysis into Nonparametric Density Estimation

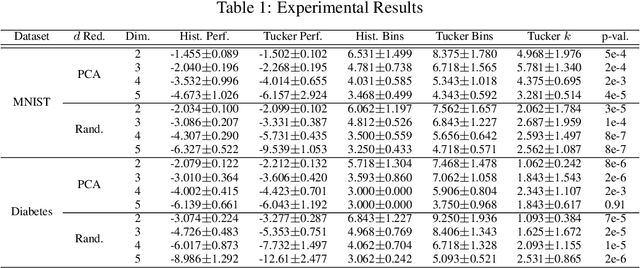
The construction and theoretical analysis of the most popular universally consistent nonparametric density estimators hinge on one functional property: smoothness. In this paper we investigate the theoretical implications of incorporating a multi-view latent variable model, a type of low-rank model, into nonparametric density estimation. To do this we perform extensive analysis on histogram-style estimators that integrate a multi-view model. Our analysis culminates in showing that there exists a universally consistent histogram-style estimator that converges to any multi-view model with a finite number of Lipschitz continuous components at a rate of $\widetilde{O}(1/\sqrt[3]{n})$ in $L^1$ error. In contrast, the standard histogram estimator can converge at a rate slower than $1/\sqrt[d]{n}$ on the same class of densities. We also introduce a new nonparametric latent variable model based on the Tucker decomposition. A rudimentary implementation of our estimators experimentally demonstrates a considerable performance improvement over the standard histogram estimator. We also provide a thorough analysis of the sample complexity of our Tucker decomposition-based model and a variety of other results. Thus, our paper provides solid theoretical foundations for extending low-rank techniques to the nonparametric setting

Learning Interpretable Concept Groups in CNNs

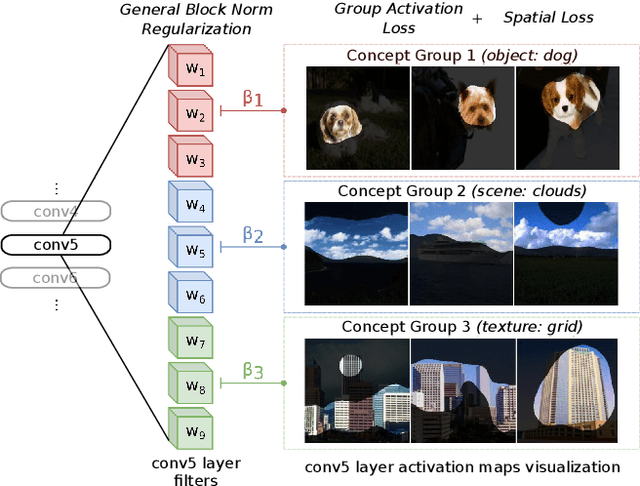
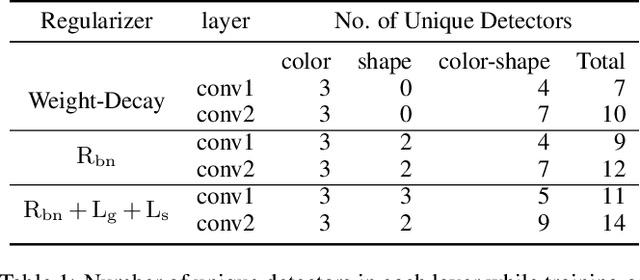
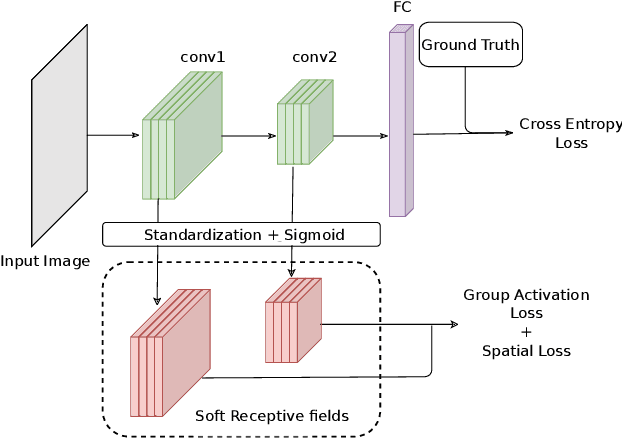
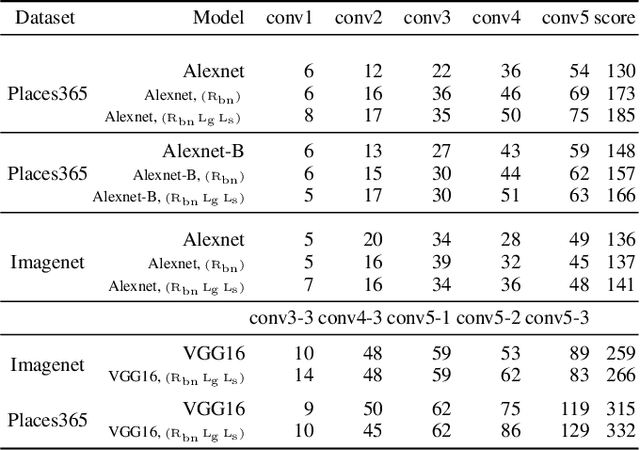
We propose a novel training methodology -- Concept Group Learning (CGL) -- that encourages training of interpretable CNN filters by partitioning filters in each layer into concept groups, each of which is trained to learn a single visual concept. We achieve this through a novel regularization strategy that forces filters in the same group to be active in similar image regions for a given layer. We additionally use a regularizer to encourage a sparse weighting of the concept groups in each layer so that a few concept groups can have greater importance than others. We quantitatively evaluate CGL's model interpretability using standard interpretability evaluation techniques and find that our method increases interpretability scores in most cases. Qualitatively we compare the image regions that are most active under filters learned using CGL versus filters learned without CGL and find that CGL activation regions more strongly concentrate around semantically relevant features.

Fine-grained Generalization Analysis of Structured Output Prediction

In machine learning we often encounter structured output prediction problems (SOPPs), i.e. problems where the output space admits a rich internal structure. Application domains where SOPPs naturally occur include natural language processing, speech recognition, and computer vision. Typical SOPPs have an extremely large label set, which grows exponentially as a function of the size of the output. Existing generalization analysis implies generalization bounds with at least a square-root dependency on the cardinality $d$ of the label set, which can be vacuous in practice. In this paper, we significantly improve the state of the art by developing novel high-probability bounds with a logarithmic dependency on $d$. Moreover, we leverage the lens of algorithmic stability to develop generalization bounds in expectation without any dependency on $d$. Our results therefore build a solid theoretical foundation for learning in large-scale SOPPs. Furthermore, we extend our results to learning with weakly dependent data.

Fine-grained Generalization Analysis of Vector-valued Learning

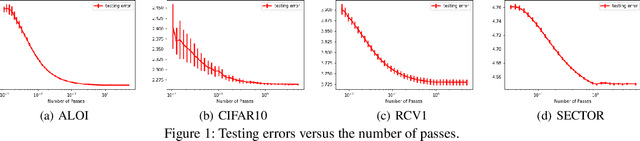
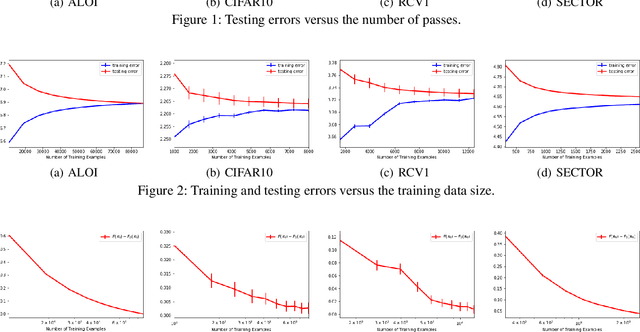
Many fundamental machine learning tasks can be formulated as a problem of learning with vector-valued functions, where we learn multiple scalar-valued functions together. Although there is some generalization analysis on different specific algorithms under the empirical risk minimization principle, a unifying analysis of vector-valued learning under a regularization framework is still lacking. In this paper, we initiate the generalization analysis of regularized vector-valued learning algorithms by presenting bounds with a mild dependency on the output dimension and a fast rate on the sample size. Our discussions relax the existing assumptions on the restrictive constraint of hypothesis spaces, smoothness of loss functions and low-noise condition. To understand the interaction between optimization and learning, we further use our results to derive the first generalization bounds for stochastic gradient descent with vector-valued functions. We apply our general results to multi-class classification and multi-label classification, which yield the first bounds with a logarithmic dependency on the output dimension for extreme multi-label classification with the Frobenius regularization. As a byproduct, we derive a Rademacher complexity bound for loss function classes defined in terms of a general strongly convex function.

Orthogonal Inductive Matrix Completion

We propose orthogonal inductive matrix completion (OMIC), an interpretable model composed of a sum of matrix completion terms, each with orthonormal side information. We can inject prior knowledge about the eigenvectors of the ground truth matrix, whilst maintaining the representation capability of the model. We present a provably converging algorithm that optimizes all components of the model simultaneously, using nuclear-norm regularisation. Our method is backed up by \textit{distribution-free} learning guarantees that improve with the quality of the injected knowledge. As a special case of our general framework, we study a model consisting of a sum of user and item biases (generic behaviour), a non-inductive term (specific behaviour), and an inductive term using side information. Our theoretical analysis shows that $\epsilon$-recovering the ground truth matrix requires at most $O\left( \frac{n+m+(\sqrt{n}+\sqrt{m})\sqrt{rmn}C}{\epsilon^2}\right)$ entries, where $r$ (resp. $C$) is the rank (resp. maximum entry) of the bias-free part of the ground truth matrix. We analyse the performance of OMIC on several synthetic and real datasets. On synthetic datasets with a sliding scale of user bias relevance, we show that OMIC better adapts to different regimes than other methods and can recover the ground truth. On real life datasets containing user/items recommendations and relevant side information, we find that OMIC surpasses the state of the art, with the added benefit of greater interpretability.

Improved Generalisation Bounds for Deep Learning Through $L^\infty$ Covering Numbers

Using proof techniques involving $L^\infty$ covering numbers, we show generalisation error bounds for deep learning with two main improvements over the state of the art. First, our bounds have no explicit dependence on the number of classes except for logarithmic factors. This holds even when formulating the bounds in terms of the $L^2$-norm of the weight matrices, while previous bounds exhibit at least a square-root dependence on the number of classes in this case. Second, we adapt the Rademacher analysis of DNNs to incorporate weight sharing---a task of fundamental theoretical importance which was previously attempted only under very restrictive assumptions. In our results, each convolutional filter contributes only once to the bound, regardless of how many times it is applied. Finally we provide a few further technical improvements, including improving the width dependence from before to after pooling. We also examine our bound's behaviour on artificial data.