Interpretable Tensor Fusion

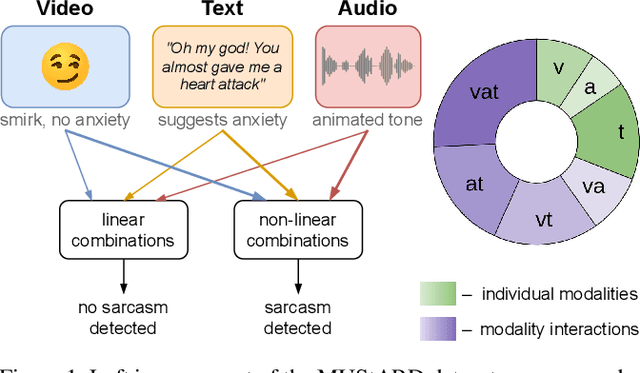
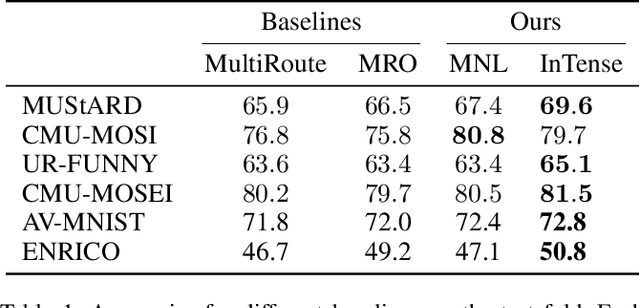
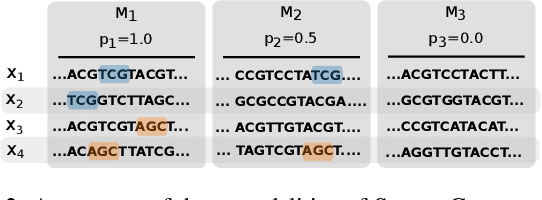
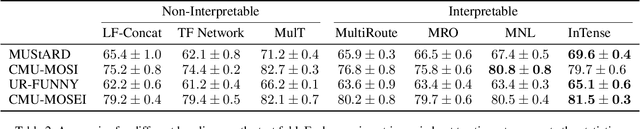
Conventional machine learning methods are predominantly designed to predict outcomes based on a single data type. However, practical applications may encompass data of diverse types, such as text, images, and audio. We introduce interpretable tensor fusion (InTense), a multimodal learning method for training neural networks to simultaneously learn multimodal data representations and their interpretable fusion. InTense can separately capture both linear combinations and multiplicative interactions of diverse data types, thereby disentangling higher-order interactions from the individual effects of each modality. InTense provides interpretability out of the box by assigning relevance scores to modalities and their associations. The approach is theoretically grounded and yields meaningful relevance scores on multiple synthetic and real-world datasets. Experiments on six real-world datasets show that InTense outperforms existing state-of-the-art multimodal interpretable approaches in terms of accuracy and interpretability.

Fine-grained Generalization Analysis of Structured Output Prediction

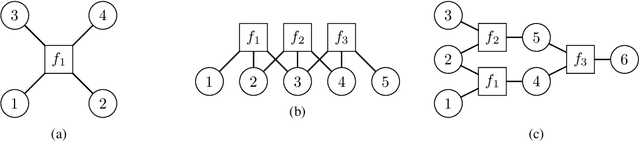
In machine learning we often encounter structured output prediction problems (SOPPs), i.e. problems where the output space admits a rich internal structure. Application domains where SOPPs naturally occur include natural language processing, speech recognition, and computer vision. Typical SOPPs have an extremely large label set, which grows exponentially as a function of the size of the output. Existing generalization analysis implies generalization bounds with at least a square-root dependency on the cardinality $d$ of the label set, which can be vacuous in practice. In this paper, we significantly improve the state of the art by developing novel high-probability bounds with a logarithmic dependency on $d$. Moreover, we leverage the lens of algorithmic stability to develop generalization bounds in expectation without any dependency on $d$. Our results therefore build a solid theoretical foundation for learning in large-scale SOPPs. Furthermore, we extend our results to learning with weakly dependent data.

Input Hessian Regularization of Neural Networks

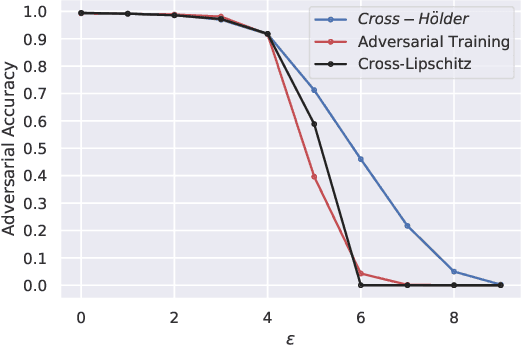
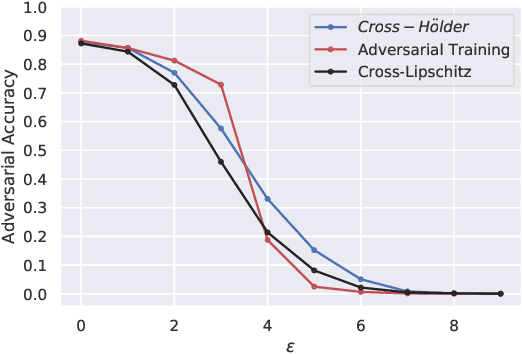
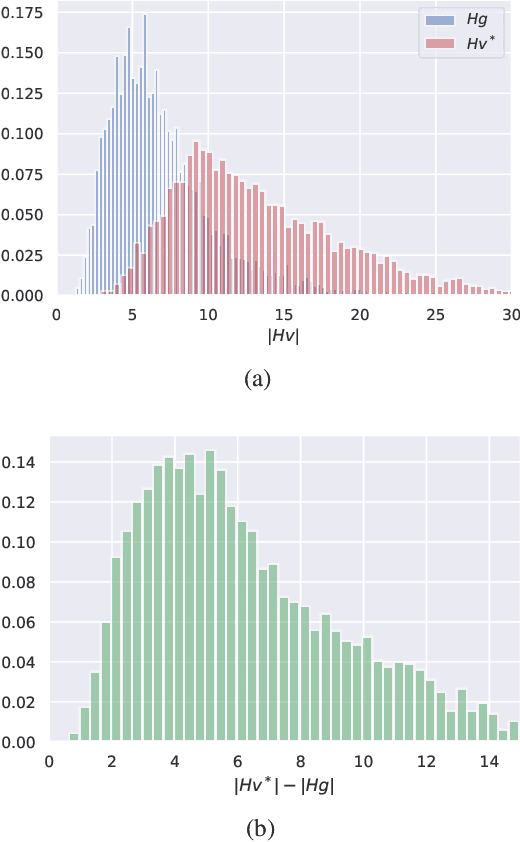
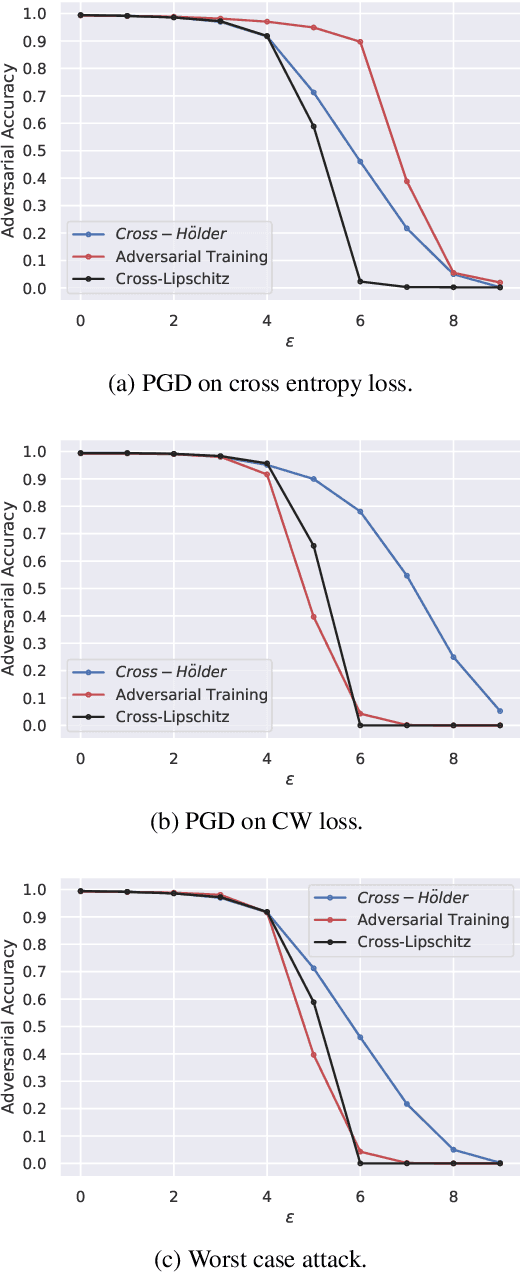
Regularizing the input gradient has shown to be effective in promoting the robustness of neural networks. The regularization of the input's Hessian is therefore a natural next step. A key challenge here is the computational complexity. Computing the Hessian of inputs is computationally infeasible. In this paper we propose an efficient algorithm to train deep neural networks with Hessian operator-norm regularization. We analyze the approach theoretically and prove that the Hessian operator norm relates to the ability of a neural network to withstand an adversarial attack. We give a preliminary experimental evaluation on the MNIST and FMNIST datasets, which demonstrates that the new regularizer can, indeed, be feasible and, furthermore, that it increases the robustness of neural networks over input gradient regularization.