Orthogonal Inductive Matrix Completion

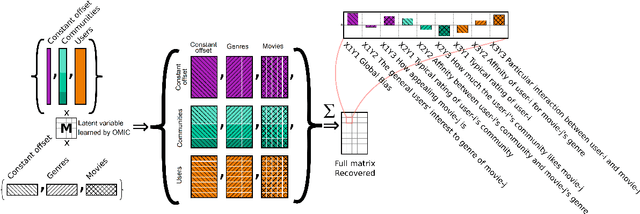
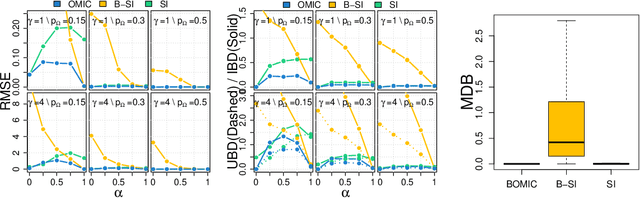
We propose orthogonal inductive matrix completion (OMIC), an interpretable model composed of a sum of matrix completion terms, each with orthonormal side information. We can inject prior knowledge about the eigenvectors of the ground truth matrix, whilst maintaining the representation capability of the model. We present a provably converging algorithm that optimizes all components of the model simultaneously, using nuclear-norm regularisation. Our method is backed up by \textit{distribution-free} learning guarantees that improve with the quality of the injected knowledge. As a special case of our general framework, we study a model consisting of a sum of user and item biases (generic behaviour), a non-inductive term (specific behaviour), and an inductive term using side information. Our theoretical analysis shows that $\epsilon$-recovering the ground truth matrix requires at most $O\left( \frac{n+m+(\sqrt{n}+\sqrt{m})\sqrt{rmn}C}{\epsilon^2}\right)$ entries, where $r$ (resp. $C$) is the rank (resp. maximum entry) of the bias-free part of the ground truth matrix. We analyse the performance of OMIC on several synthetic and real datasets. On synthetic datasets with a sliding scale of user bias relevance, we show that OMIC better adapts to different regimes than other methods and can recover the ground truth. On real life datasets containing user/items recommendations and relevant side information, we find that OMIC surpasses the state of the art, with the added benefit of greater interpretability.