Generalization Bounds for Semi-supervised Matrix Completion with Distributional Side Information

We study a matrix completion problem where both the ground truth $R$ matrix and the unknown sampling distribution $P$ over observed entries are low-rank matrices, and \textit{share a common subspace}. We assume that a large amount $M$ of \textit{unlabeled} data drawn from the sampling distribution $P$ is available, together with a small amount $N$ of labeled data drawn from the same distribution and noisy estimates of the corresponding ground truth entries. This setting is inspired by recommender systems scenarios where the unlabeled data corresponds to `implicit feedback' (consisting in interactions such as purchase, click, etc. ) and the labeled data corresponds to the `explicit feedback', consisting of interactions where the user has given an explicit rating to the item. Leveraging powerful results from the theory of low-rank subspace recovery, together with classic generalization bounds for matrix completion models, we show error bounds consisting of a sum of two error terms scaling as $\widetilde{O}\left(\sqrt{\frac{nd}{M}}\right)$ and $\widetilde{O}\left(\sqrt{\frac{dr}{N}}\right)$ respectively, where $d$ is the rank of $P$ and $r$ is the rank of $M$. In synthetic experiments, we confirm that the true generalization error naturally splits into independent error terms corresponding to the estimations of $P$ and and the ground truth matrix $\ground$ respectively. In real-life experiments on Douban and MovieLens with most explicit ratings removed, we demonstrate that the method can outperform baselines relying only on the explicit ratings, demonstrating that our assumptions provide a valid toy theoretical setting to study the interaction between explicit and implicit feedbacks in recommender systems.

Generalization Analysis for Deep Contrastive Representation Learning

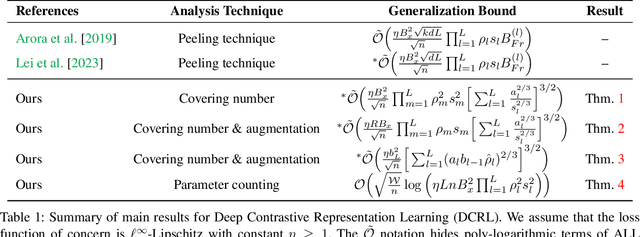
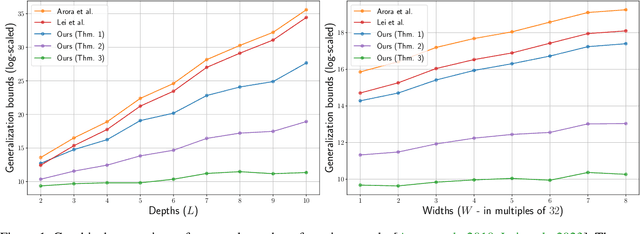
In this paper, we present generalization bounds for the unsupervised risk in the Deep Contrastive Representation Learning framework, which employs deep neural networks as representation functions. We approach this problem from two angles. On the one hand, we derive a parameter-counting bound that scales with the overall size of the neural networks. On the other hand, we provide a norm-based bound that scales with the norms of neural networks' weight matrices. Ignoring logarithmic factors, the bounds are independent of $k$, the size of the tuples provided for contrastive learning. To the best of our knowledge, this property is only shared by one other work, which employed a different proof strategy and suffers from very strong exponential dependence on the depth of the network which is due to a use of the peeling technique. Our results circumvent this by leveraging powerful results on covering numbers with respect to uniform norms over samples. In addition, we utilize loss augmentation techniques to further reduce the dependency on matrix norms and the implicit dependence on network depth. In fact, our techniques allow us to produce many bounds for the contrastive learning setting with similar architectural dependencies as in the study of the sample complexity of ordinary loss functions, thereby bridging the gap between the learning theories of contrastive learning and DNNs.