Testing for context-dependent changes in neural encoding in naturalistic experiments

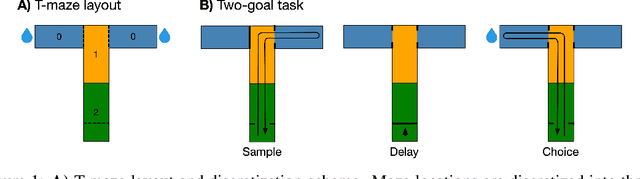
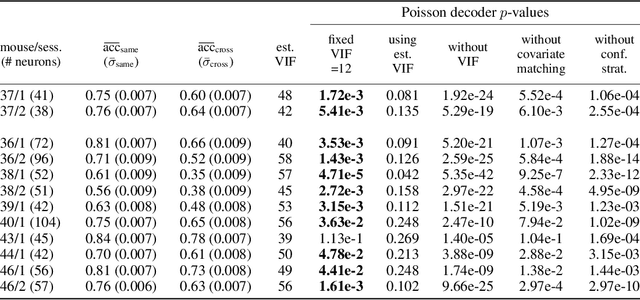
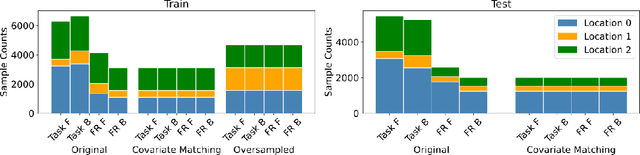
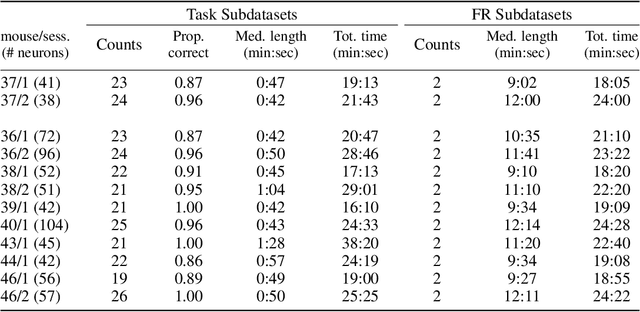
We propose a decoding-based approach to detect context effects on neural codes in longitudinal neural recording data. The approach is agnostic to how information is encoded in neural activity, and can control for a variety of possible confounding factors present in the data. We demonstrate our approach by determining whether it is possible to decode location encoding from prefrontal cortex in the mouse and, further, testing whether the encoding changes due to task engagement.

VICE: Variational Interpretable Concept Embeddings

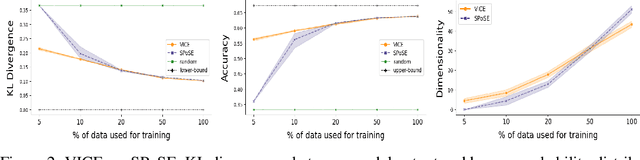
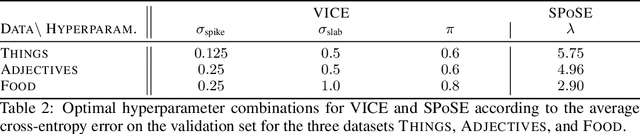
A central goal in the cognitive sciences is the development of computational models of mental representations of object concepts. This paper introduces Variational Interpretable Concept Embeddings (VICE), an approximate Bayesian method for learning interpretable object concept embeddings from human behavior in an odd-one-out triplet task. We use variational inference to obtain a sparse, non-negative solution with uncertainty estimates about each embedding value. We exploit these estimates to select the dimensions that explain the data automatically. We introduce a PAC learning bound for VICE that can be used to estimate generalization performance or determine a sufficient sample size for different experimental designs. VICE rivals or outperforms its predecessor, SPoSE, at predicting human behavior in the odd-one-out triplet task. Furthermore, VICE object representations are substantially more reproducible and consistent across random initializations.

Revealing interpretable object representations from human behavior

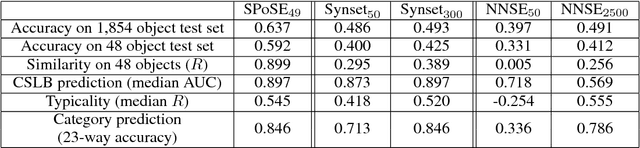
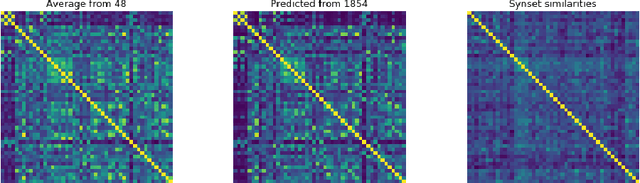
To study how mental object representations are related to behavior, we estimated sparse, non-negative representations of objects using human behavioral judgments on images representative of 1,854 object categories. These representations predicted a latent similarity structure between objects, which captured most of the explainable variance in human behavioral judgments. Individual dimensions in the low-dimensional embedding were found to be highly reproducible and interpretable as conveying degrees of taxonomic membership, functionality, and perceptual attributes. We further demonstrated the predictive power of the embeddings for explaining other forms of human behavior, including categorization, typicality judgments, and feature ratings, suggesting that the dimensions reflect human conceptual representations of objects beyond the specific task.

Distributed Weight Consolidation: A Brain Segmentation Case Study

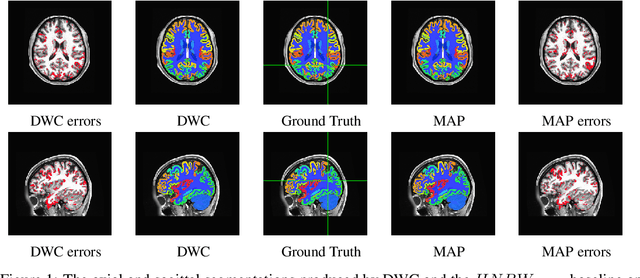
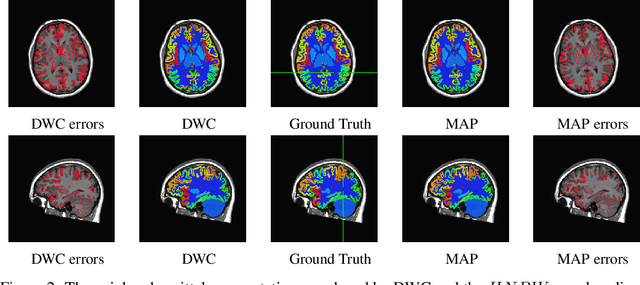
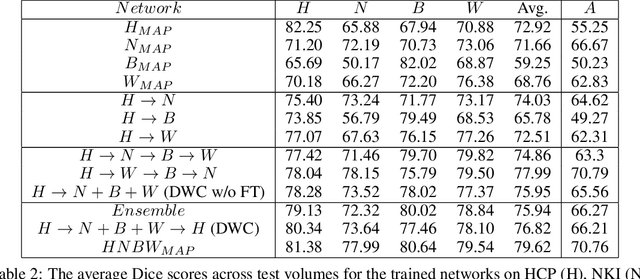
Collecting the large datasets needed to train deep neural networks can be very difficult, particularly for the many applications for which sharing and pooling data is complicated by practical, ethical, or legal concerns. However, it may be the case that derivative datasets or predictive models developed within individual sites can be shared and combined with fewer restrictions. Training on distributed data and combining the resulting networks is often viewed as continual learning, but these methods require networks to be trained sequentially. In this paper, we introduce distributed weight consolidation (DWC), a continual learning method to consolidate the weights of separate neural networks, each trained on an independent dataset. We evaluated DWC with a brain segmentation case study, where we consolidated dilated convolutional neural networks trained on independent structural magnetic resonance imaging (sMRI) datasets from different sites. We found that DWC led to increased performance on test sets from the different sites, while maintaining generalization performance for a very large and completely independent multi-site dataset, compared to an ensemble baseline.

Estimating mutual information in high dimensions via classification error

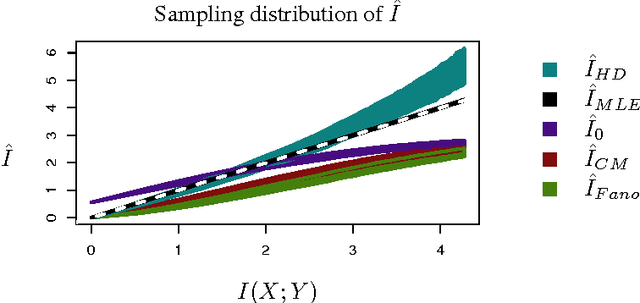
Multivariate pattern analyses approaches in neuroimaging are fundamentally concerned with investigating the quantity and type of information processed by various regions of the human brain; typically, estimates of classification accuracy are used to quantify information. While a extensive and powerful library of methods can be applied to train and assess classifiers, it is not always clear how to use the resulting measures of classification performance to draw scientific conclusions: e.g. for the purpose of evaluating redundancy between brain regions. An additional confound for interpreting classification performance is the dependence of the error rate on the number and choice of distinct classes obtained for the classification task. In contrast, mutual information is a quantity defined independently of the experimental design, and has ideal properties for comparative analyses. Unfortunately, estimating the mutual information based on observations becomes statistically infeasible in high dimensions without some kind of assumption or prior. In this paper, we construct a novel classification-based estimator of mutual information based on high-dimensional asymptotics. We show that in a particular limiting regime, the mutual information is an invertible function of the expected $k$-class Bayes error. While the theory is based on a large-sample, high-dimensional limit, we demonstrate through simulations that our proposed estimator has superior performance to the alternatives in problems of moderate dimensionality.

How many faces can be recognized? Performance extrapolation for multi-class classification

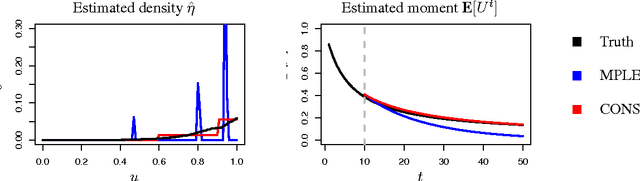
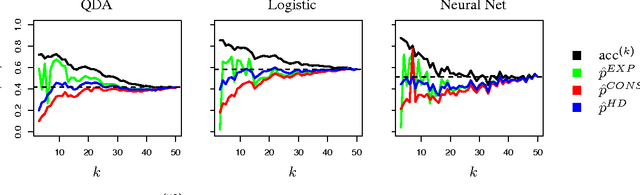
The difficulty of multi-class classification generally increases with the number of classes. Using data from a subset of the classes, can we predict how well a classifier will scale with an increased number of classes? Under the assumption that the classes are sampled exchangeably, and under the assumption that the classifier is generative (e.g. QDA or Naive Bayes), we show that the expected accuracy when the classifier is trained on $k$ classes is the $k-1$st moment of a \emph{conditional accuracy distribution}, which can be estimated from data. This provides the theoretical foundation for performance extrapolation based on pseudolikelihood, unbiased estimation, and high-dimensional asymptotics. We investigate the robustness of our methods to non-generative classifiers in simulations and one optical character recognition example.