Class Distribution Shifts in Zero-Shot Learning: Learning Robust Representations

Distribution shifts between training and deployment data often affect the performance of machine learning models. In this paper, we explore a setting where a hidden variable induces a shift in the distribution of classes. These distribution shifts are particularly challenging for zero-shot classifiers, as they rely on representations learned from training classes, but are deployed on new, unseen ones. We introduce an algorithm to learn data representations that are robust to such class distribution shifts in zero-shot verification tasks. We show that our approach, which combines hierarchical data sampling with out-of-distribution generalization techniques, improves generalization to diverse class distributions in both simulations and real-world datasets.

Confident Feature Ranking

Interpretation of feature importance values often relies on the relative order of the features rather than on the value itself, referred to as ranking. However, the order may be unstable due to the small sample sizes used in calculating the importance values. We propose that post-hoc importance methods produce a ranking and simultaneous confident intervals for the rankings. Based on pairwise comparisons of the feature importance values, our method is guaranteed to include the ``true'' (infinite sample) ranking with high probability and allows for selecting top-k sets.

Logistic Regression Equivalence: A Framework for Comparing Logistic Regression Models Across Populations

In this paper we discuss how to evaluate the differences between fitted logistic regression models across sub-populations. Our motivating example is in studying computerized diagnosis for learning disabilities, where sub-populations based on gender may or may not require separate models. In this context, significance tests for hypotheses of no difference between populations may provide perverse incentives, as larger variances and smaller samples increase the probability of not-rejecting the null. We argue that equivalence testing for a prespecified tolerance level on population differences incentivizes accuracy in the inference. We develop a cascading set of equivalence tests, in which each test addresses a different aspect of the model: the way the phenomenon is coded in the regression coefficients, the individual predictions in the per example log odds ratio and the overall accuracy in the mean square prediction error. For each equivalence test, we propose a strategy for setting the equivalence thresholds. The large-sample approximations are validated using simulations. For diagnosis data, we show examples for equivalent and non-equivalent models.

Predicting Classification Accuracy when Adding New Unobserved Classes

Multiclass classifiers are often designed and evaluated only on a sample from the classes on which they will eventually be applied. Hence, their final accuracy remains unknown. In this work we study how a classifier's performance over the initial class sample can be used to extrapolate its expected accuracy on a larger, unobserved set of classes. For this, we define a measure of separation between correct and incorrect classes that is independent of the number of classes: the reversed ROC (rROC), which is obtained by replacing the roles of classes and data-points in the common ROC. We show that the classification accuracy is a function of the rROC in multiclass classifiers, for which the learned representation of data from the initial class sample remains unchanged when new classes are added. Using these results we formulate a robust neural-network-based algorithm, CleaneX, which learns to estimate the accuracy of such classifiers on arbitrarily large sets of classes. Our method achieves remarkably better predictions than current state-of-the-art methods on both simulations and real datasets of object detection, face recognition, and brain decoding.

Extrapolating Expected Accuracies for Large Multi-Class Problems

The difficulty of multi-class classification generally increases with the number of classes. Using data from a subset of the classes, can we predict how well a classifier will scale with an increased number of classes? Under the assumptions that the classes are sampled identically and independently from a population, and that the classifier is based on independently learned scoring functions, we show that the expected accuracy when the classifier is trained on k classes is the (k-1)st moment of a certain distribution that can be estimated from data. We present an unbiased estimation method based on the theory, and demonstrate its application on a facial recognition example.

Estimating mutual information in high dimensions via classification error

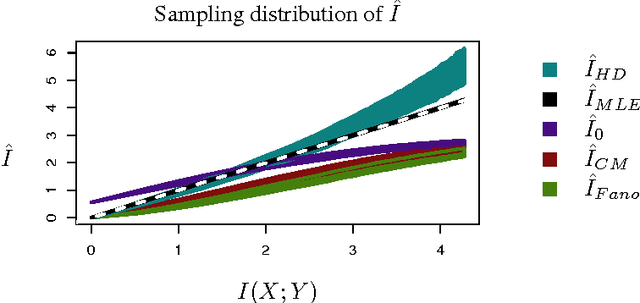
Multivariate pattern analyses approaches in neuroimaging are fundamentally concerned with investigating the quantity and type of information processed by various regions of the human brain; typically, estimates of classification accuracy are used to quantify information. While a extensive and powerful library of methods can be applied to train and assess classifiers, it is not always clear how to use the resulting measures of classification performance to draw scientific conclusions: e.g. for the purpose of evaluating redundancy between brain regions. An additional confound for interpreting classification performance is the dependence of the error rate on the number and choice of distinct classes obtained for the classification task. In contrast, mutual information is a quantity defined independently of the experimental design, and has ideal properties for comparative analyses. Unfortunately, estimating the mutual information based on observations becomes statistically infeasible in high dimensions without some kind of assumption or prior. In this paper, we construct a novel classification-based estimator of mutual information based on high-dimensional asymptotics. We show that in a particular limiting regime, the mutual information is an invertible function of the expected $k$-class Bayes error. While the theory is based on a large-sample, high-dimensional limit, we demonstrate through simulations that our proposed estimator has superior performance to the alternatives in problems of moderate dimensionality.

How many faces can be recognized? Performance extrapolation for multi-class classification

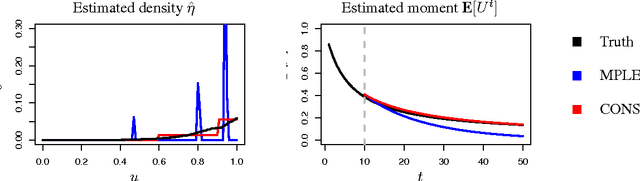
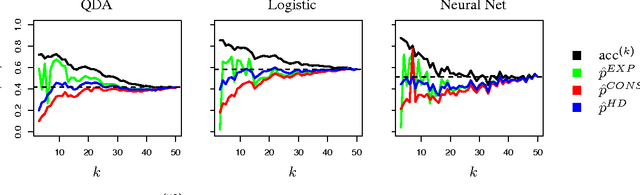
The difficulty of multi-class classification generally increases with the number of classes. Using data from a subset of the classes, can we predict how well a classifier will scale with an increased number of classes? Under the assumption that the classes are sampled exchangeably, and under the assumption that the classifier is generative (e.g. QDA or Naive Bayes), we show that the expected accuracy when the classifier is trained on $k$ classes is the $k-1$st moment of a \emph{conditional accuracy distribution}, which can be estimated from data. This provides the theoretical foundation for performance extrapolation based on pseudolikelihood, unbiased estimation, and high-dimensional asymptotics. We investigate the robustness of our methods to non-generative classifiers in simulations and one optical character recognition example.