How many faces can be recognized? Performance extrapolation for multi-class classification
Paper and Code
Jun 16, 2016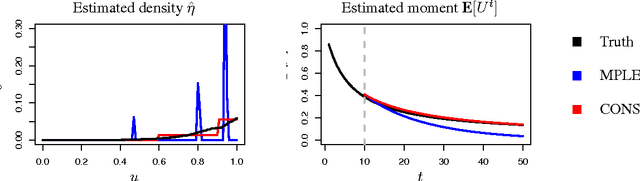

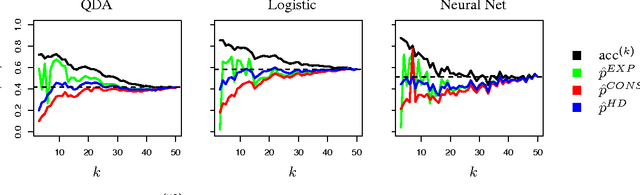
The difficulty of multi-class classification generally increases with the number of classes. Using data from a subset of the classes, can we predict how well a classifier will scale with an increased number of classes? Under the assumption that the classes are sampled exchangeably, and under the assumption that the classifier is generative (e.g. QDA or Naive Bayes), we show that the expected accuracy when the classifier is trained on $k$ classes is the $k-1$st moment of a \emph{conditional accuracy distribution}, which can be estimated from data. This provides the theoretical foundation for performance extrapolation based on pseudolikelihood, unbiased estimation, and high-dimensional asymptotics. We investigate the robustness of our methods to non-generative classifiers in simulations and one optical character recognition example.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge