Knowing what you know in brain segmentation using deep neural networks

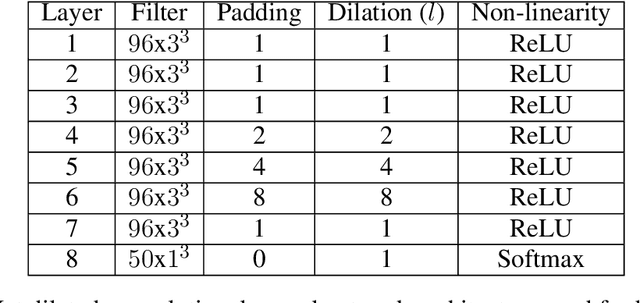
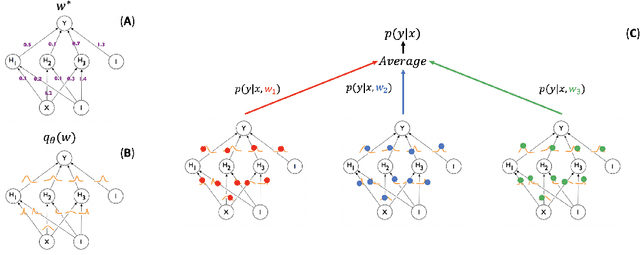
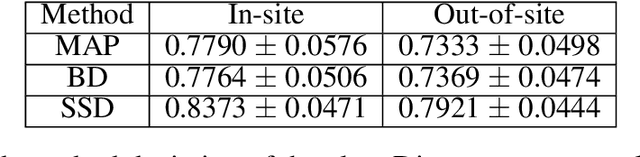
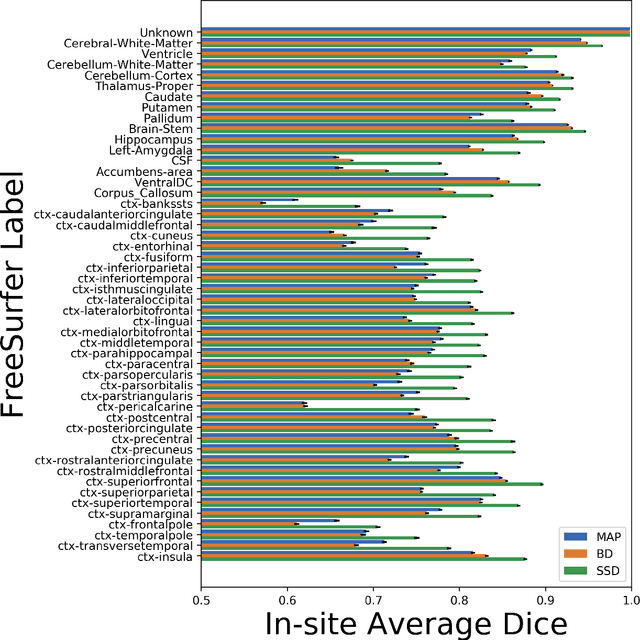
In this paper, we describe a deep neural network trained to predict FreeSurfer segmentations of structural MRI volumes, in seconds rather than hours. The network was trained and evaluated on an extremely large dataset (n = 11,148), obtained by combining data from more than a hundred sites. We also show that the prediction uncertainty of the network at each voxel is a good indicator of whether the network has made an error. The resulting uncertainty volume can be used in conjunction with the predicted segmentation to improve downstream uses, such as calculation of measures derived from segmentation regions of interest or the building of prediction models. Finally, we demonstrate that the average prediction uncertainty across voxels in the brain is an excellent indicator of manual quality control ratings, outperforming the best available automated solutions.

Extrapolating Expected Accuracies for Large Multi-Class Problems

The difficulty of multi-class classification generally increases with the number of classes. Using data from a subset of the classes, can we predict how well a classifier will scale with an increased number of classes? Under the assumptions that the classes are sampled identically and independently from a population, and that the classifier is based on independently learned scoring functions, we show that the expected accuracy when the classifier is trained on k classes is the (k-1)st moment of a certain distribution that can be estimated from data. We present an unbiased estimation method based on the theory, and demonstrate its application on a facial recognition example.

Learning Summary Statistic for Approximate Bayesian Computation via Deep Neural Network

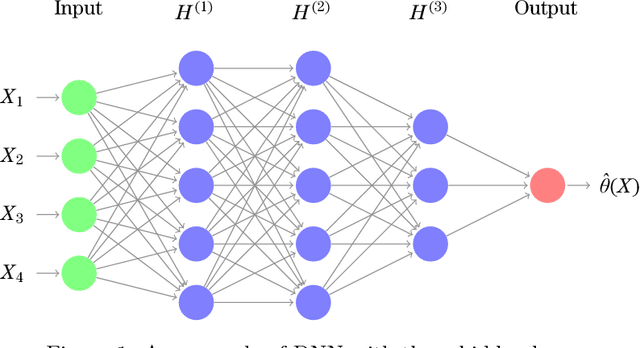
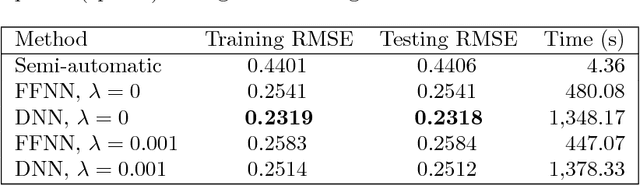
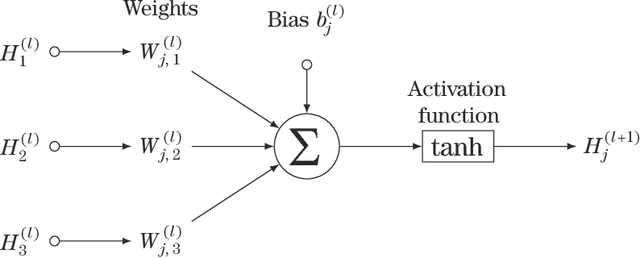
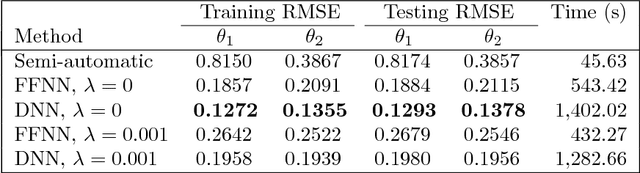
Approximate Bayesian Computation (ABC) methods are used to approximate posterior distributions in models with unknown or computationally intractable likelihoods. Both the accuracy and computational efficiency of ABC depend on the choice of summary statistic, but outside of special cases where the optimal summary statistics are known, it is unclear which guiding principles can be used to construct effective summary statistics. In this paper we explore the possibility of automating the process of constructing summary statistics by training deep neural networks to predict the parameters from artificially generated data: the resulting summary statistics are approximately posterior means of the parameters. With minimal model-specific tuning, our method constructs summary statistics for the Ising model and the moving-average model, which match or exceed theoretically-motivated summary statistics in terms of the accuracies of the resulting posteriors.

Quantifying error in estimates of human brain fiber directions using Earth Mover's Distance

Diffusion-weighted MR imaging (DWI) is the only method we currently have to measure connections between different parts of the human brain in vivo. To elucidate the structure of these connections, algorithms for tracking bundles of axonal fibers through the subcortical white matter rely on local estimates of the fiber orientation distribution function (fODF) in different parts of the brain. These functions describe the relative abundance of populations of axonal fibers crossing each other in each location. Multiple models exist for estimating fODFs. The quality of the resulting estimates can be quantified by means of a suitable measure of distance on the space of fODFs. However, there are multiple distance metrics that can be applied for this purpose, including smoothed $L_p$ distances and the Wasserstein metrics. Here, we give four reasons for the use of the Earth Mover's Distance (EMD) equipped with the arc-length, as a distance metric. (continued)

Deconvolution of High-Dimensional Mixtures via Boosting, with Application to Diffusion-Weighted MRI of Human Brain

Diffusion-weighted magnetic resonance imaging (DWI) and fiber tractography are the only methods to measure the structure of the white matter in the living human brain. The diffusion signal has been modelled as the combined contribution from many individual fascicles of nerve fibers passing through each location in the white matter. Typically, this is done via basis pursuit, but estimation of the exact directions is limited due to discretization. The difficulties inherent in modeling DWI data are shared by many other problems involving fitting non-parametric mixture models. Ekanadaham et al. proposed an approach, continuous basis pursuit, to overcome discretization error in the 1-dimensional case (e.g., spike-sorting). Here, we propose a more general algorithm that fits mixture models of any dimensionality without discretization. Our algorithm uses the principles of L2-boost, together with refitting of the weights and pruning of the parameters. The addition of these steps to L2-boost both accelerates the algorithm and assures its accuracy. We refer to the resulting algorithm as elastic basis pursuit, or EBP, since it expands and contracts the active set of kernels as needed. We show that in contrast to existing approaches to fitting mixtures, our boosting framework (1) enables the selection of the optimal bias-variance tradeoff along the solution path, and (2) scales with high-dimensional problems. In simulations of DWI, we find that EBP yields better parameter estimates than a non-negative least squares (NNLS) approach, or the standard model used in DWI, the tensor model, which serves as the basis for diffusion tensor imaging (DTI). We demonstrate the utility of the method in DWI data acquired in parts of the brain containing crossings of multiple fascicles of nerve fibers.