Fractional ridge regression: a fast, interpretable reparameterization of ridge regression

Ridge regression (RR) is a regularization technique that penalizes the L2-norm of the coefficients in linear regression. One of the challenges of using RR is the need to set a hyperparameter ($\alpha$) that controls the amount of regularization. Cross-validation is typically used to select the best $\alpha$ from a set of candidates. However, efficient and appropriate selection of $\alpha$ can be challenging, particularly where large amounts of data are analyzed. Because the selected $\alpha$ depends on the scale of the data and predictors, it is not straightforwardly interpretable. Here, we propose to reparameterize RR in terms of the ratio $\gamma$ between the L2-norms of the regularized and unregularized coefficients. This approach, called fractional RR (FRR), has several benefits: the solutions obtained for different $\gamma$ are guaranteed to vary, guarding against wasted calculations, and automatically span the relevant range of regularization, avoiding the need for arduous manual exploration. We provide an algorithm to solve FRR, as well as open-source software implementations in Python and MATLAB (https://github.com/nrdg/fracridge). We show that the proposed method is fast and scalable for large-scale data problems, and delivers results that are straightforward to interpret and compare across models and datasets.

Fitting IVIM with Variable Projection and Simplicial Optimization

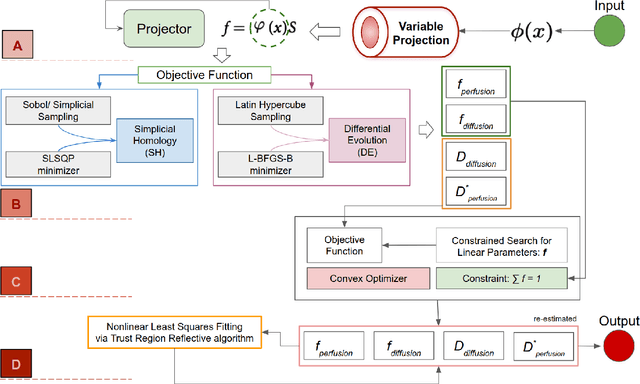
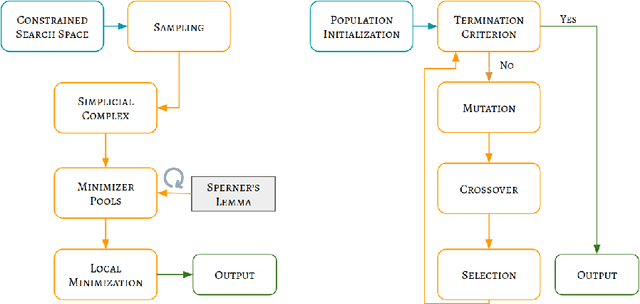
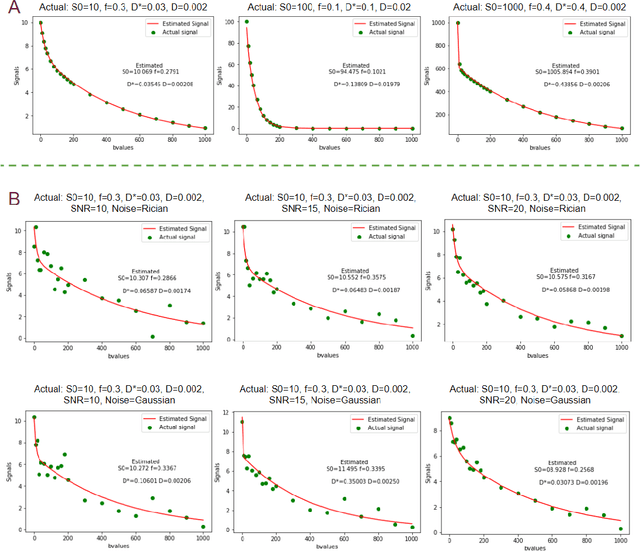
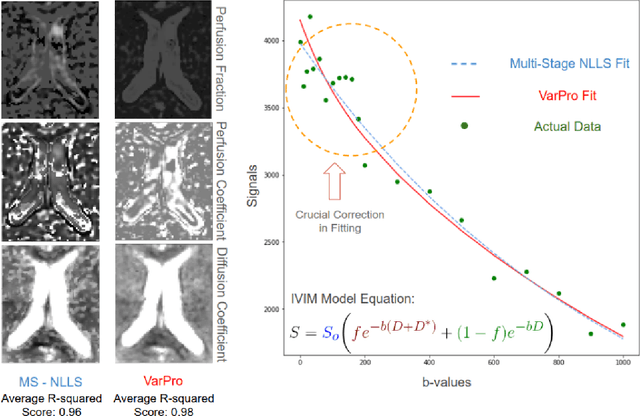
Fitting multi-exponential models to Diffusion MRI (dMRI) data has always been challenging due to various underlying complexities. In this work, we introduce a novel and robust fitting framework for the standard two-compartment IVIM microstructural model. This framework provides a significant improvement over the existing methods and helps estimate the associated diffusion and perfusion parameters of IVIM in an automatic manner. As a part of this work we provide capabilities to switch between more advanced global optimization methods such as simplicial homology (SH) and differential evolution (DE). Our experiments show that the results obtained from this simultaneous fitting procedure disentangle the model parameters in a reduced subspace. The proposed framework extends the seminal work originated in the MIX framework, with improved procedures for multi-stage fitting. This framework has been made available as an open-source Python implementation and disseminated to the community through the DIPY project.

Forecasting Future Humphrey Visual Fields Using Deep Learning

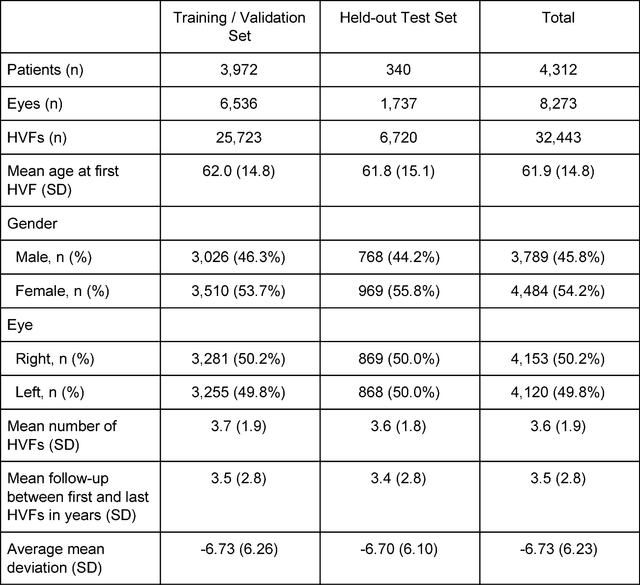
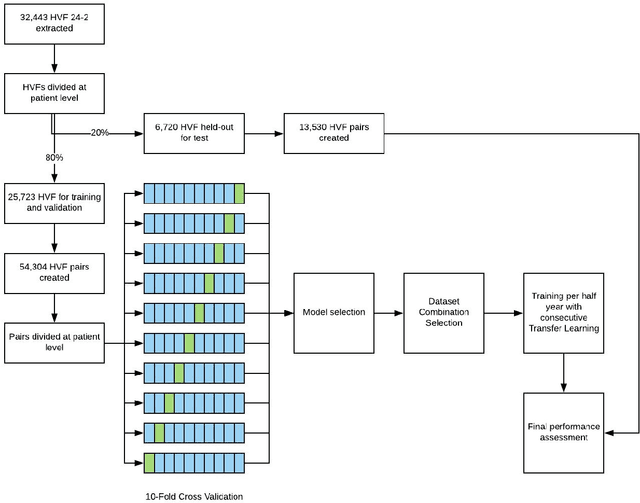
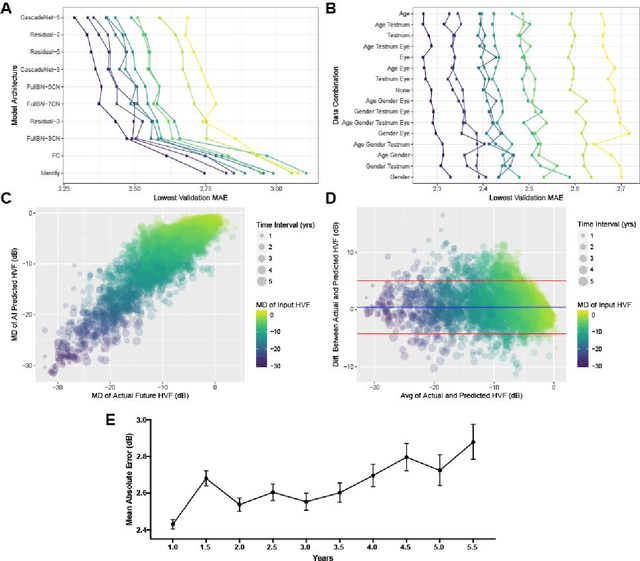
Purpose: To determine if deep learning networks could be trained to forecast a future 24-2 Humphrey Visual Field (HVF). Participants: All patients who obtained a HVF 24-2 at the University of Washington. Methods: All datapoints from consecutive 24-2 HVFs from 1998 to 2018 were extracted from a University of Washington database. Ten-fold cross validation with a held out test set was used to develop the three main phases of model development: model architecture selection, dataset combination selection, and time-interval model training with transfer learning, to train a deep learning artificial neural network capable of generating a point-wise visual field prediction. Results: More than 1.7 million perimetry points were extracted to the hundredth decibel from 32,443 24-2 HVFs. The best performing model with 20 million trainable parameters, CascadeNet-5, was selected. The overall MAE for the test set was 2.47 dB (95% CI: 2.45 dB to 2.48 dB). The 100 fully trained models were able to successfully predict progressive field loss in glaucomatous eyes up to 5.5 years in the future with a correlation of 0.92 between the MD of predicted and actual future HVF (p < 2.2 x 10 -16 ) and an average difference of 0.41 dB. Conclusions: Using unfiltered real-world datasets, deep learning networks show an impressive ability to not only learn spatio-temporal HVF changes but also to generate predictions for future HVFs up to 5.5 years, given only a single HVF.

Quantifying error in estimates of human brain fiber directions using Earth Mover's Distance

Diffusion-weighted MR imaging (DWI) is the only method we currently have to measure connections between different parts of the human brain in vivo. To elucidate the structure of these connections, algorithms for tracking bundles of axonal fibers through the subcortical white matter rely on local estimates of the fiber orientation distribution function (fODF) in different parts of the brain. These functions describe the relative abundance of populations of axonal fibers crossing each other in each location. Multiple models exist for estimating fODFs. The quality of the resulting estimates can be quantified by means of a suitable measure of distance on the space of fODFs. However, there are multiple distance metrics that can be applied for this purpose, including smoothed $L_p$ distances and the Wasserstein metrics. Here, we give four reasons for the use of the Earth Mover's Distance (EMD) equipped with the arc-length, as a distance metric. (continued)

Deconvolution of High-Dimensional Mixtures via Boosting, with Application to Diffusion-Weighted MRI of Human Brain

Diffusion-weighted magnetic resonance imaging (DWI) and fiber tractography are the only methods to measure the structure of the white matter in the living human brain. The diffusion signal has been modelled as the combined contribution from many individual fascicles of nerve fibers passing through each location in the white matter. Typically, this is done via basis pursuit, but estimation of the exact directions is limited due to discretization. The difficulties inherent in modeling DWI data are shared by many other problems involving fitting non-parametric mixture models. Ekanadaham et al. proposed an approach, continuous basis pursuit, to overcome discretization error in the 1-dimensional case (e.g., spike-sorting). Here, we propose a more general algorithm that fits mixture models of any dimensionality without discretization. Our algorithm uses the principles of L2-boost, together with refitting of the weights and pruning of the parameters. The addition of these steps to L2-boost both accelerates the algorithm and assures its accuracy. We refer to the resulting algorithm as elastic basis pursuit, or EBP, since it expands and contracts the active set of kernels as needed. We show that in contrast to existing approaches to fitting mixtures, our boosting framework (1) enables the selection of the optimal bias-variance tradeoff along the solution path, and (2) scales with high-dimensional problems. In simulations of DWI, we find that EBP yields better parameter estimates than a non-negative least squares (NNLS) approach, or the standard model used in DWI, the tensor model, which serves as the basis for diffusion tensor imaging (DTI). We demonstrate the utility of the method in DWI data acquired in parts of the brain containing crossings of multiple fascicles of nerve fibers.