Learning Summary Statistic for Approximate Bayesian Computation via Deep Neural Network

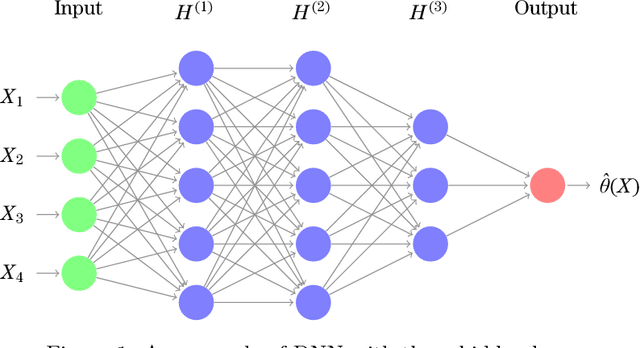
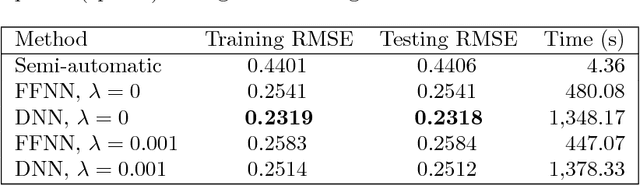
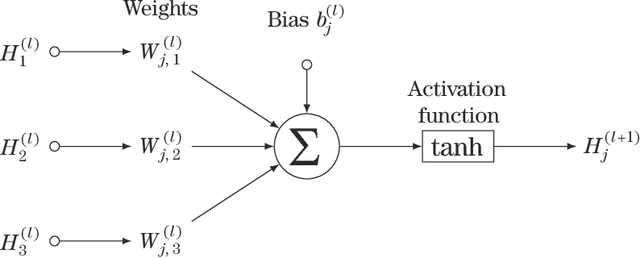
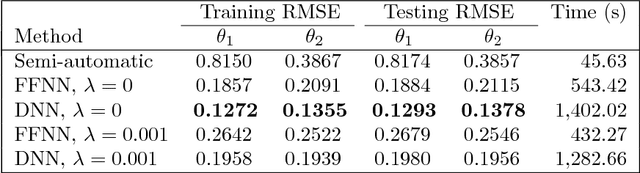
Approximate Bayesian Computation (ABC) methods are used to approximate posterior distributions in models with unknown or computationally intractable likelihoods. Both the accuracy and computational efficiency of ABC depend on the choice of summary statistic, but outside of special cases where the optimal summary statistics are known, it is unclear which guiding principles can be used to construct effective summary statistics. In this paper we explore the possibility of automating the process of constructing summary statistics by training deep neural networks to predict the parameters from artificially generated data: the resulting summary statistics are approximately posterior means of the parameters. With minimal model-specific tuning, our method constructs summary statistics for the Ising model and the moving-average model, which match or exceed theoretically-motivated summary statistics in terms of the accuracies of the resulting posteriors.

Convergence of Contrastive Divergence with Annealed Learning Rate in Exponential Family

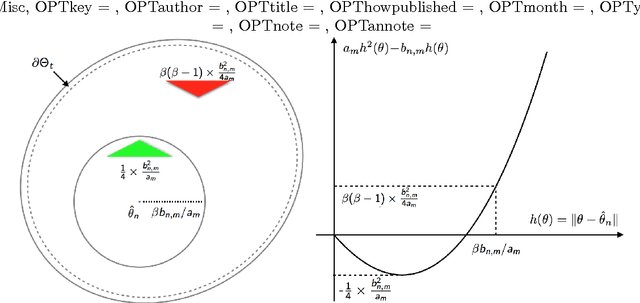
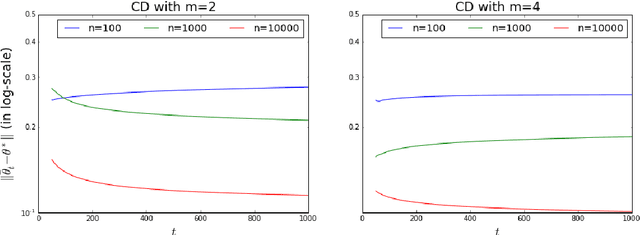
In our recent paper, we showed that in exponential family, contrastive divergence (CD) with fixed learning rate will give asymptotically consistent estimates \cite{wu2016convergence}. In this paper, we establish consistency and convergence rate of CD with annealed learning rate $\eta_t$. Specifically, suppose CD-$m$ generates the sequence of parameters $\{\theta_t\}_{t \ge 0}$ using an i.i.d. data sample $\mathbf{X}_1^n \sim p_{\theta^*}$ of size $n$, then $\delta_n(\mathbf{X}_1^n) = \limsup_{t \to \infty} \Vert \sum_{s=t_0}^t \eta_s \theta_s / \sum_{s=t_0}^t \eta_s - \theta^* \Vert$ converges in probability to 0 at a rate of $1/\sqrt[3]{n}$. The number ($m$) of MCMC transitions in CD only affects the coefficient factor of convergence rate. Our proof is not a simple extension of the one in \cite{wu2016convergence}. which depends critically on the fact that $\{\theta_t\}_{t \ge 0}$ is a homogeneous Markov chain conditional on the observed sample $\mathbf{X}_1^n$. Under annealed learning rate, the homogeneous Markov property is not available and we have to develop an alternative approach based on super-martingales. Experiment results of CD on a fully-visible $2\times 2$ Boltzmann Machine are provided to demonstrate our theoretical results.