Convergence of Contrastive Divergence with Annealed Learning Rate in Exponential Family
Paper and Code
May 20, 2016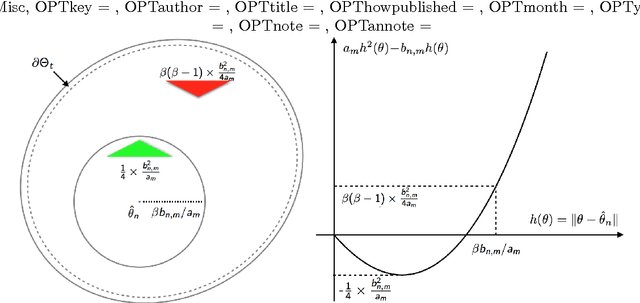
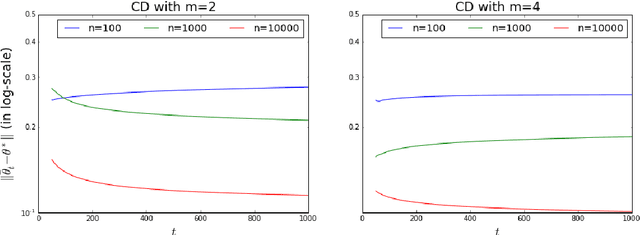
In our recent paper, we showed that in exponential family, contrastive divergence (CD) with fixed learning rate will give asymptotically consistent estimates \cite{wu2016convergence}. In this paper, we establish consistency and convergence rate of CD with annealed learning rate $\eta_t$. Specifically, suppose CD-$m$ generates the sequence of parameters $\{\theta_t\}_{t \ge 0}$ using an i.i.d. data sample $\mathbf{X}_1^n \sim p_{\theta^*}$ of size $n$, then $\delta_n(\mathbf{X}_1^n) = \limsup_{t \to \infty} \Vert \sum_{s=t_0}^t \eta_s \theta_s / \sum_{s=t_0}^t \eta_s - \theta^* \Vert$ converges in probability to 0 at a rate of $1/\sqrt[3]{n}$. The number ($m$) of MCMC transitions in CD only affects the coefficient factor of convergence rate. Our proof is not a simple extension of the one in \cite{wu2016convergence}. which depends critically on the fact that $\{\theta_t\}_{t \ge 0}$ is a homogeneous Markov chain conditional on the observed sample $\mathbf{X}_1^n$. Under annealed learning rate, the homogeneous Markov property is not available and we have to develop an alternative approach based on super-martingales. Experiment results of CD on a fully-visible $2\times 2$ Boltzmann Machine are provided to demonstrate our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge