Mini-batch Metropolis-Hastings MCMC with Reversible SGLD Proposal

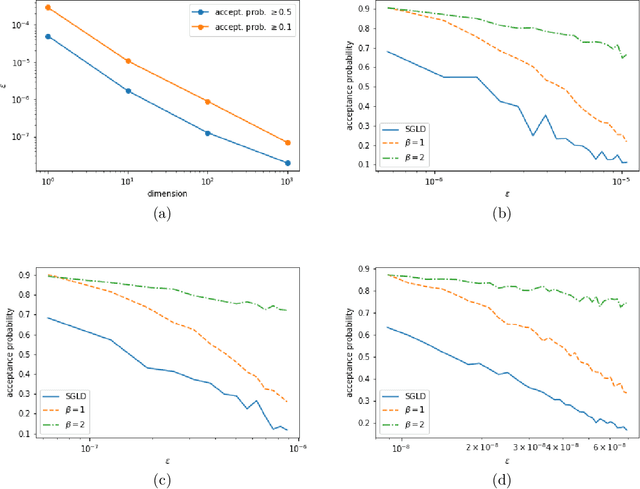
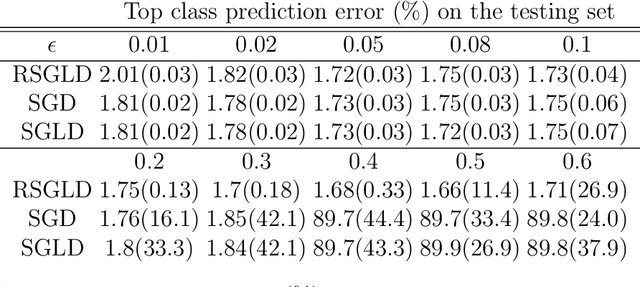
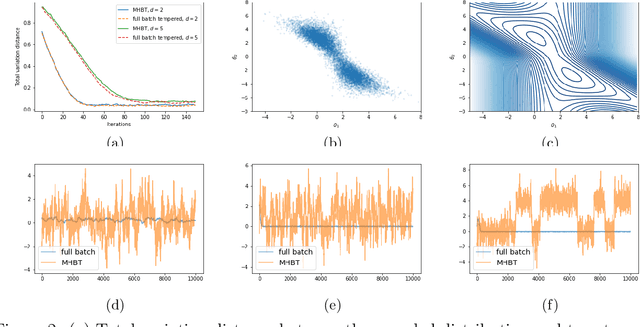
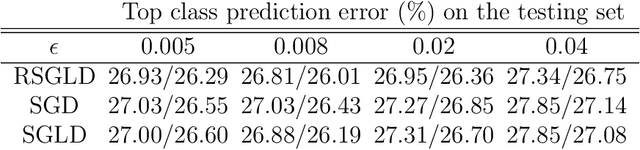
Traditional MCMC algorithms are computationally intensive and do not scale well to large data. In particular, the Metropolis-Hastings (MH) algorithm requires passing over the entire dataset to evaluate the likelihood ratio in each iteration. We propose a general framework for performing MH-MCMC using mini-batches of the whole dataset and show that this gives rise to approximately a tempered stationary distribution. We prove that the algorithm preserves the modes of the original target distribution and derive an error bound on the approximation with mild assumptions on the likelihood. To further extend the utility of the algorithm to high dimensional settings, we construct a proposal with forward and reverse moves using stochastic gradient and show that the construction leads to reasonable acceptance probabilities. We demonstrate the performance of our algorithm in both low dimensional models and high dimensional neural network applications. Particularly in the latter case, compared to popular optimization methods, our method is more robust to the choice of learning rate and improves testing accuracy.

Convergence of Contrastive Divergence Algorithm in Exponential Family

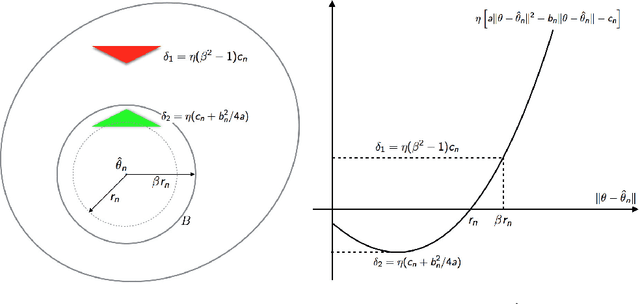
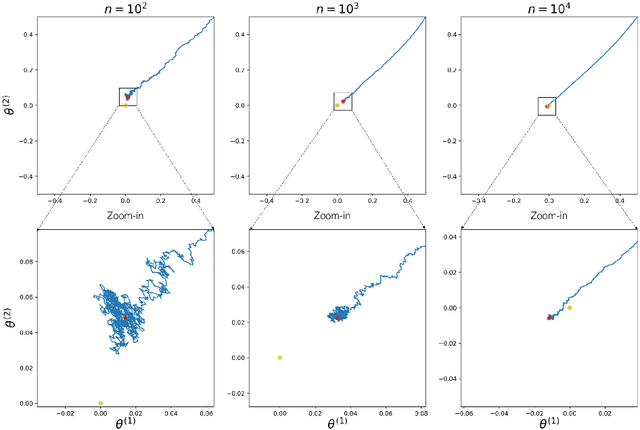
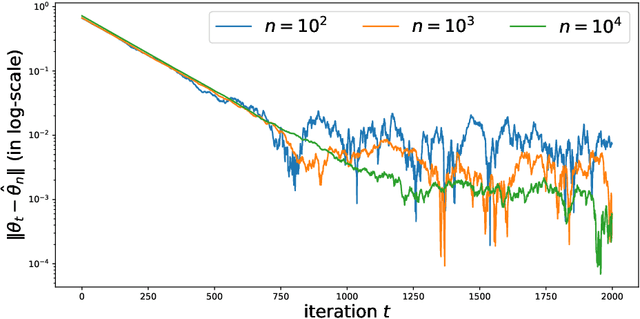
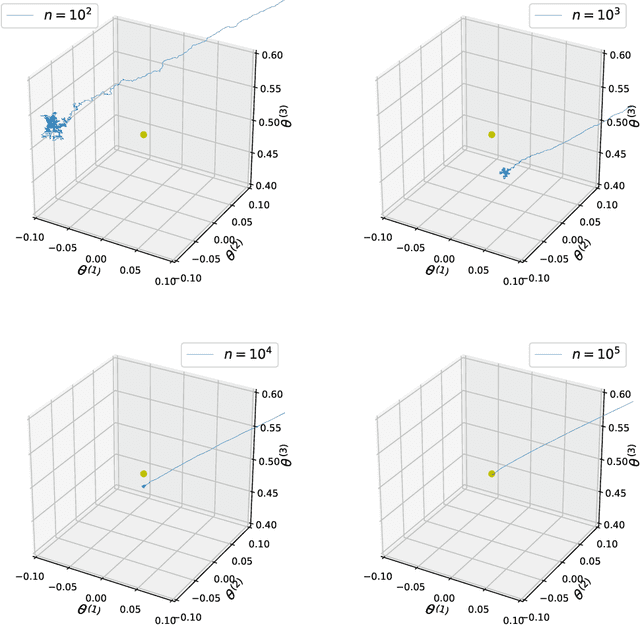
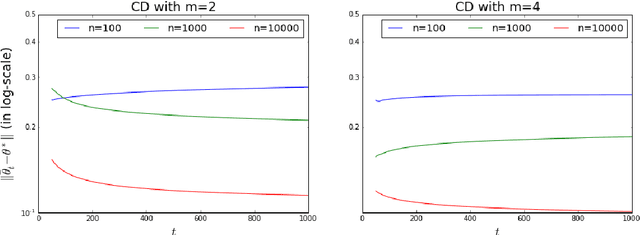
The Contrastive Divergence (CD) algorithm has achieved notable success in training energy-based models including Restricted Boltzmann Machines and played a key role in the emergence of deep learning. The idea of this algorithm is to approximate the intractable term in the exact gradient of the log-likelihood function by using short Markov chain Monte Carlo (MCMC) runs. The approximate gradient is computationally-cheap but biased. Whether and why the CD algorithm provides an asymptotically consistent estimate are still open questions. This paper studies the asymptotic properties of the CD algorithm in canonical exponential families, which are special cases of the energy-based model. Suppose the CD algorithm runs $m$ MCMC transition steps at each iteration $t$ and iteratively generates a sequence of parameter estimates $\{\theta_t\}_{t \ge 0}$ given an i.i.d. data sample $\{X_i\}_{i=1}^n \sim p_{\theta_\star}$. Under conditions which are commonly obeyed by the CD algorithm in practice, we prove the existence of some bounded $m$ such that any limit point of the time average $\left. \sum_{s=0}^{t-1} \theta_s \right/ t$ as $t \to \infty$ is a consistent estimate for the true parameter $\theta_\star$. Our proof is based on the fact that $\{\theta_t\}_{t \ge 0}$ is a homogenous Markov chain conditional on the data sample $\{X_i\}_{i=1}^n$. This chain meets the Foster-Lyapunov drift criterion and converges to a random walk around the Maximum Likelihood Estimate. The range of the random walk shrinks to zero at rate $\mathcal{O}(1/\sqrt[3]{n})$ as the sample size $n \to \infty$.

Learning Summary Statistic for Approximate Bayesian Computation via Deep Neural Network

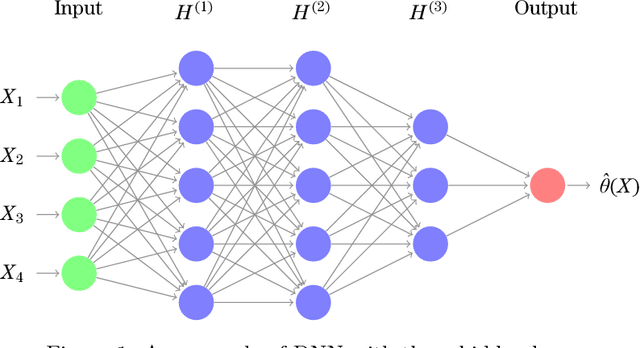
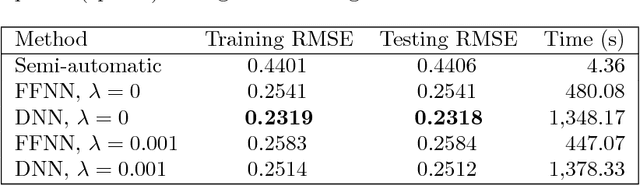
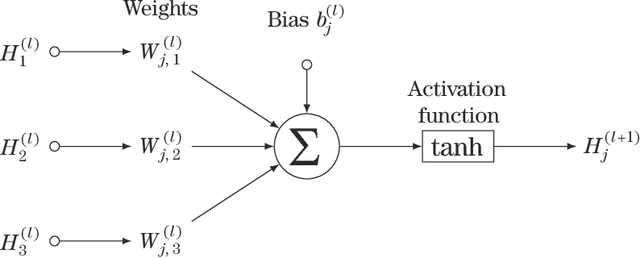
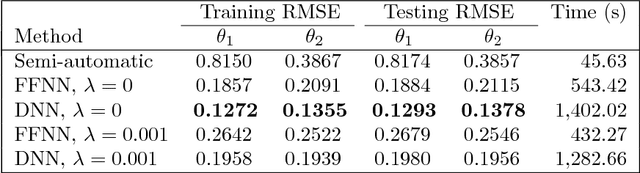
Approximate Bayesian Computation (ABC) methods are used to approximate posterior distributions in models with unknown or computationally intractable likelihoods. Both the accuracy and computational efficiency of ABC depend on the choice of summary statistic, but outside of special cases where the optimal summary statistics are known, it is unclear which guiding principles can be used to construct effective summary statistics. In this paper we explore the possibility of automating the process of constructing summary statistics by training deep neural networks to predict the parameters from artificially generated data: the resulting summary statistics are approximately posterior means of the parameters. With minimal model-specific tuning, our method constructs summary statistics for the Ising model and the moving-average model, which match or exceed theoretically-motivated summary statistics in terms of the accuracies of the resulting posteriors.

Convergence of Contrastive Divergence with Annealed Learning Rate in Exponential Family

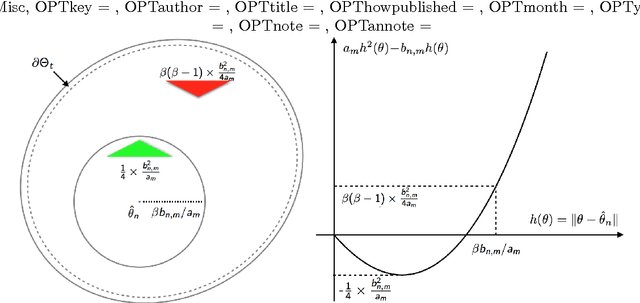
In our recent paper, we showed that in exponential family, contrastive divergence (CD) with fixed learning rate will give asymptotically consistent estimates \cite{wu2016convergence}. In this paper, we establish consistency and convergence rate of CD with annealed learning rate $\eta_t$. Specifically, suppose CD-$m$ generates the sequence of parameters $\{\theta_t\}_{t \ge 0}$ using an i.i.d. data sample $\mathbf{X}_1^n \sim p_{\theta^*}$ of size $n$, then $\delta_n(\mathbf{X}_1^n) = \limsup_{t \to \infty} \Vert \sum_{s=t_0}^t \eta_s \theta_s / \sum_{s=t_0}^t \eta_s - \theta^* \Vert$ converges in probability to 0 at a rate of $1/\sqrt[3]{n}$. The number ($m$) of MCMC transitions in CD only affects the coefficient factor of convergence rate. Our proof is not a simple extension of the one in \cite{wu2016convergence}. which depends critically on the fact that $\{\theta_t\}_{t \ge 0}$ is a homogeneous Markov chain conditional on the observed sample $\mathbf{X}_1^n$. Under annealed learning rate, the homogeneous Markov property is not available and we have to develop an alternative approach based on super-martingales. Experiment results of CD on a fully-visible $2\times 2$ Boltzmann Machine are provided to demonstrate our theoretical results.