U-shaped and Inverted-U Scaling behind Emergent Abilities of Large Language Models

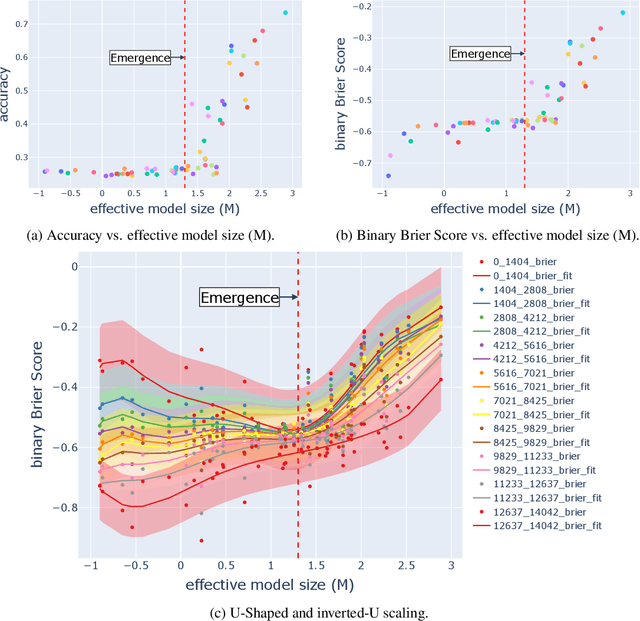
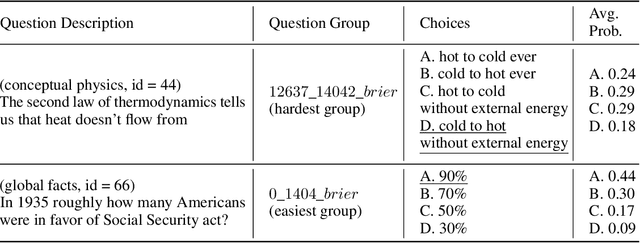
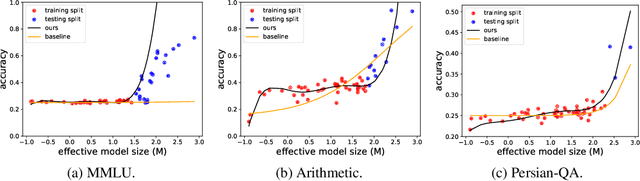
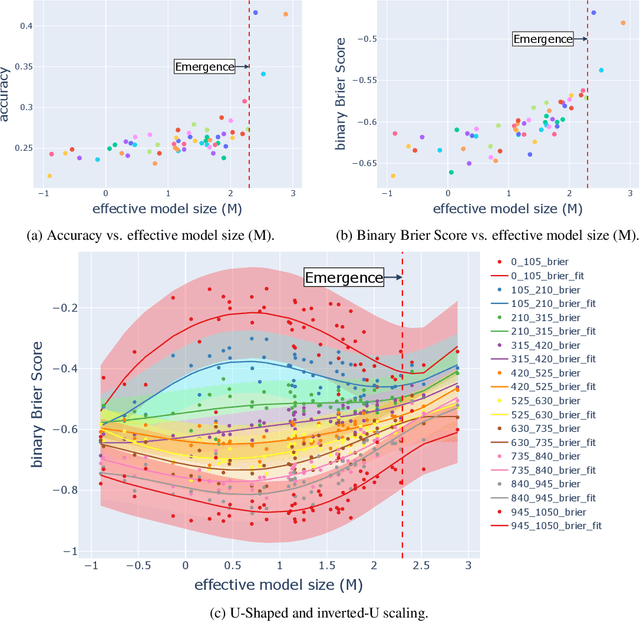
Large language models (LLMs) have been shown to exhibit emergent abilities in some downstream tasks, where performance seems to stagnate at first and then improve sharply and unpredictably with scale beyond a threshold. By dividing questions in the datasets according to difficulty level by average performance, we observe U-shaped scaling for hard questions, and inverted-U scaling followed by steady improvement for easy questions. Moreover, the emergence threshold roughly coincides with the point at which performance on easy questions reverts from inverse scaling to standard scaling. Capitalizing on the observable though opposing scaling trend on easy and hard questions, we propose a simple yet effective pipeline, called Slice-and-Sandwich, to predict both the emergence threshold and model performance beyond the threshold.

AND: Audio Network Dissection for Interpreting Deep Acoustic Models

Neuron-level interpretations aim to explain network behaviors and properties by investigating neurons responsive to specific perceptual or structural input patterns. Although there is emerging work in the vision and language domains, none is explored for acoustic models. To bridge the gap, we introduce $\textit{AND}$, the first $\textbf{A}$udio $\textbf{N}$etwork $\textbf{D}$issection framework that automatically establishes natural language explanations of acoustic neurons based on highly-responsive audio. $\textit{AND}$ features the use of LLMs to summarize mutual acoustic features and identities among audio. Extensive experiments are conducted to verify $\textit{AND}$'s precise and informative descriptions. In addition, we demonstrate a potential use of $\textit{AND}$ for audio machine unlearning by conducting concept-specific pruning based on the generated descriptions. Finally, we highlight two acoustic model behaviors with analysis by $\textit{AND}$: (i) models discriminate audio with a combination of basic acoustic features rather than high-level abstract concepts; (ii) training strategies affect model behaviors and neuron interpretability -- supervised training guides neurons to gradually narrow their attention, while self-supervised learning encourages neurons to be polysemantic for exploring high-level features.

DOrA: 3D Visual Grounding with Order-Aware Referring

3D visual grounding aims to identify the target object within a 3D point cloud scene referred to by a natural language description. While previous works attempt to exploit the verbo-visual relation with proposed cross-modal transformers, unstructured natural utterances and scattered objects might lead to undesirable performances. In this paper, we introduce DOrA, a novel 3D visual grounding framework with Order-Aware referring. DOrA is designed to leverage Large Language Models (LLMs) to parse language description, suggesting a referential order of anchor objects. Such ordered anchor objects allow DOrA to update visual features and locate the target object during the grounding process. Experimental results on the NR3D and ScanRefer datasets demonstrate our superiority in both low-resource and full-data scenarios. In particular, DOrA surpasses current state-of-the-art frameworks by 9.3% and 7.8% grounding accuracy under 1% data and 10% data settings, respectively.

Model Extraction Attack against Self-supervised Speech Models

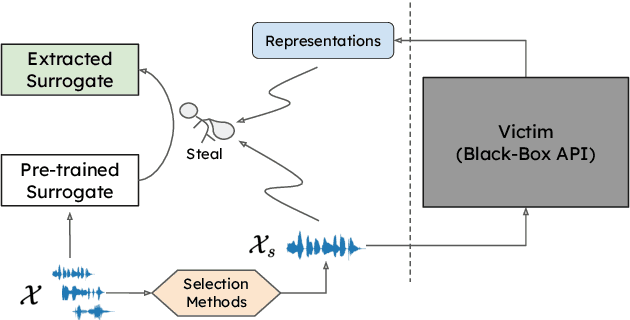
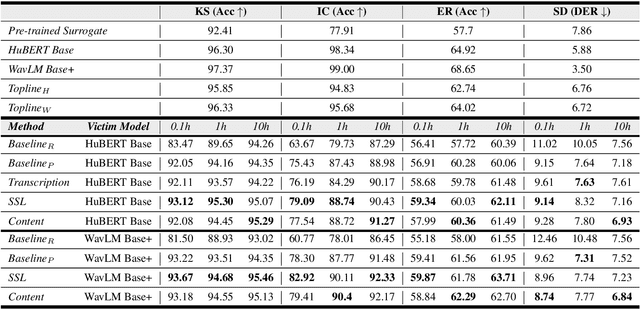
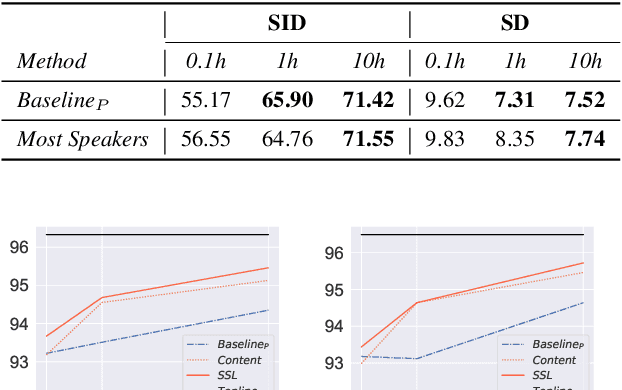
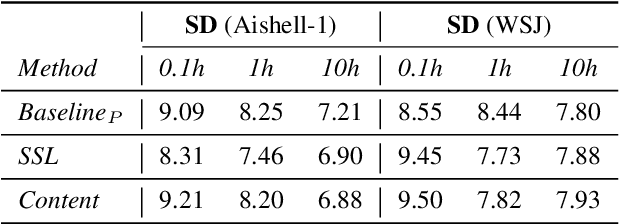
Self-supervised learning (SSL) speech models generate meaningful representations of given clips and achieve incredible performance across various downstream tasks. Model extraction attack (MEA) often refers to an adversary stealing the functionality of the victim model with only query access. In this work, we study the MEA problem against SSL speech model with a small number of queries. We propose a two-stage framework to extract the model. In the first stage, SSL is conducted on the large-scale unlabeled corpus to pre-train a small speech model. Secondly, we actively sample a small portion of clips from the unlabeled corpus and query the target model with these clips to acquire their representations as labels for the small model's second-stage training. Experiment results show that our sampling methods can effectively extract the target model without knowing any information about its model architecture.

The Ability of Self-Supervised Speech Models for Audio Representations

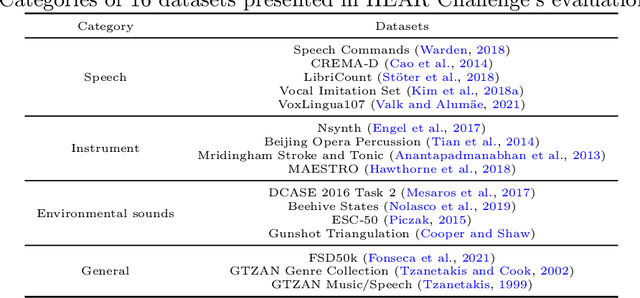
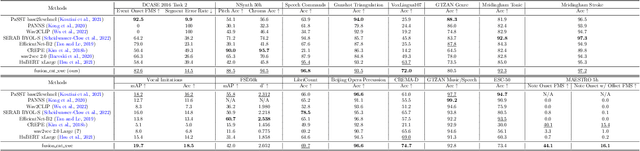
Self-supervised learning (SSL) speech models have achieved unprecedented success in speech representation learning, but some questions regarding their representation ability remain unanswered. This paper addresses two of them: (1) Can SSL speech models deal with non-speech audio?; (2) Would different SSL speech models have insights into diverse aspects of audio features? To answer the two questions, we conduct extensive experiments on abundant speech and non-speech audio datasets to evaluate the representation ability of currently state-of-the-art SSL speech models, which are wav2vec 2.0 and HuBERT in this paper. These experiments are carried out during NeurIPS 2021 HEAR Challenge as a standard evaluation pipeline provided by competition officials. Results show that (1) SSL speech models could extract meaningful features of a wide range of non-speech audio, while they may also fail on certain types of datasets; (2) different SSL speech models have insights into different aspects of audio features. The two conclusions provide a foundation for the ensemble of representation models. We further propose an ensemble framework to fuse speech representation models' embeddings. Our framework outperforms state-of-the-art SSL speech/audio models and has generally superior performance on abundant datasets compared with other teams in HEAR Challenge. Our code is available at https://github.com/tony10101105/HEAR-2021-NeurIPS-Challenge -- NTU-GURA.

Mini-batch Metropolis-Hastings MCMC with Reversible SGLD Proposal

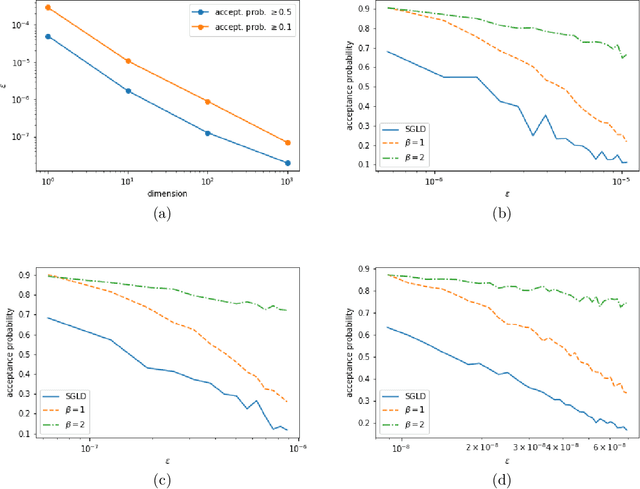
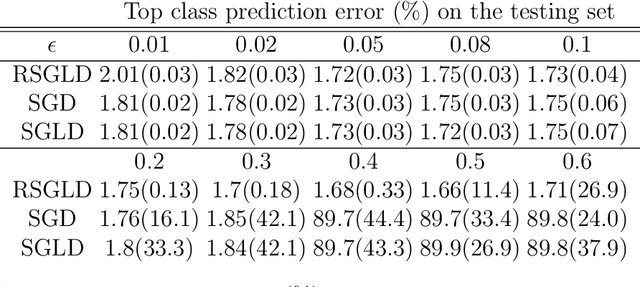
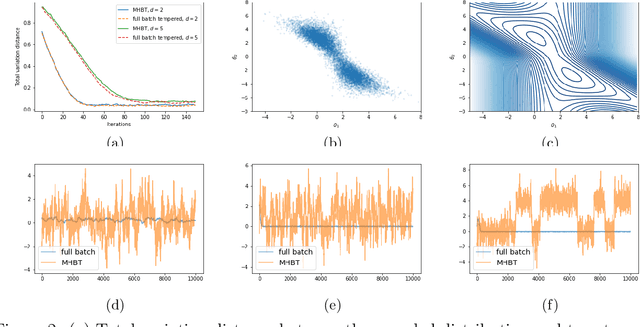
Traditional MCMC algorithms are computationally intensive and do not scale well to large data. In particular, the Metropolis-Hastings (MH) algorithm requires passing over the entire dataset to evaluate the likelihood ratio in each iteration. We propose a general framework for performing MH-MCMC using mini-batches of the whole dataset and show that this gives rise to approximately a tempered stationary distribution. We prove that the algorithm preserves the modes of the original target distribution and derive an error bound on the approximation with mild assumptions on the likelihood. To further extend the utility of the algorithm to high dimensional settings, we construct a proposal with forward and reverse moves using stochastic gradient and show that the construction leads to reasonable acceptance probabilities. We demonstrate the performance of our algorithm in both low dimensional models and high dimensional neural network applications. Particularly in the latter case, compared to popular optimization methods, our method is more robust to the choice of learning rate and improves testing accuracy.

Convergence of Contrastive Divergence Algorithm in Exponential Family

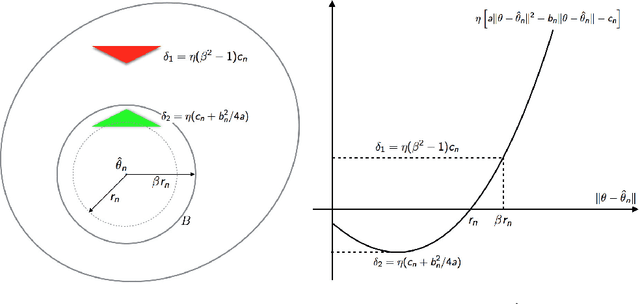
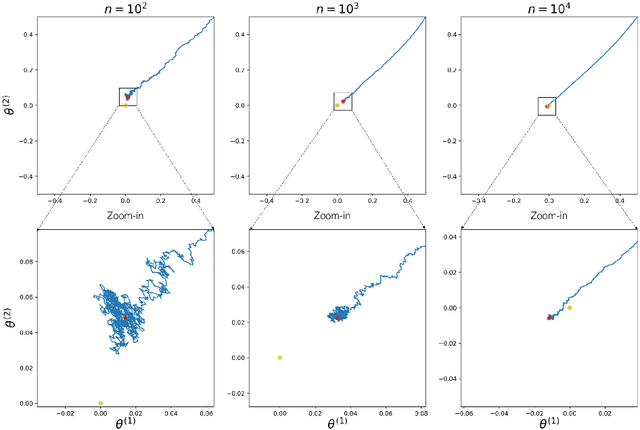
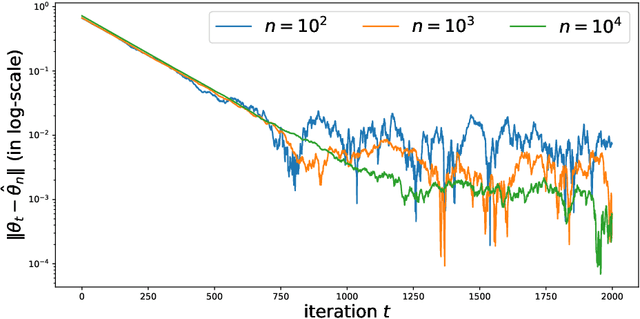
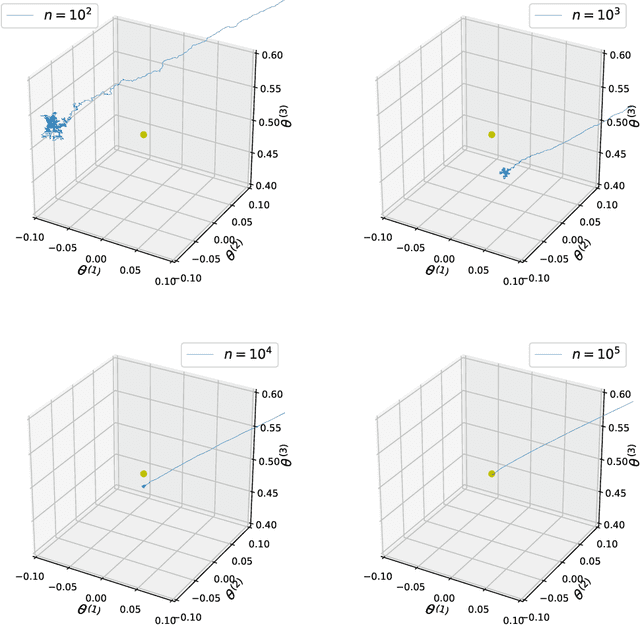
The Contrastive Divergence (CD) algorithm has achieved notable success in training energy-based models including Restricted Boltzmann Machines and played a key role in the emergence of deep learning. The idea of this algorithm is to approximate the intractable term in the exact gradient of the log-likelihood function by using short Markov chain Monte Carlo (MCMC) runs. The approximate gradient is computationally-cheap but biased. Whether and why the CD algorithm provides an asymptotically consistent estimate are still open questions. This paper studies the asymptotic properties of the CD algorithm in canonical exponential families, which are special cases of the energy-based model. Suppose the CD algorithm runs $m$ MCMC transition steps at each iteration $t$ and iteratively generates a sequence of parameter estimates $\{\theta_t\}_{t \ge 0}$ given an i.i.d. data sample $\{X_i\}_{i=1}^n \sim p_{\theta_\star}$. Under conditions which are commonly obeyed by the CD algorithm in practice, we prove the existence of some bounded $m$ such that any limit point of the time average $\left. \sum_{s=0}^{t-1} \theta_s \right/ t$ as $t \to \infty$ is a consistent estimate for the true parameter $\theta_\star$. Our proof is based on the fact that $\{\theta_t\}_{t \ge 0}$ is a homogenous Markov chain conditional on the data sample $\{X_i\}_{i=1}^n$. This chain meets the Foster-Lyapunov drift criterion and converges to a random walk around the Maximum Likelihood Estimate. The range of the random walk shrinks to zero at rate $\mathcal{O}(1/\sqrt[3]{n})$ as the sample size $n \to \infty$.