Mini-batch Metropolis-Hastings MCMC with Reversible SGLD Proposal
Paper and Code
Aug 28, 2019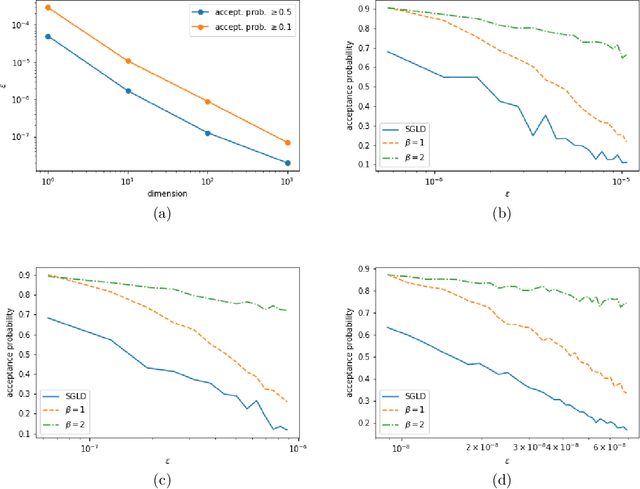
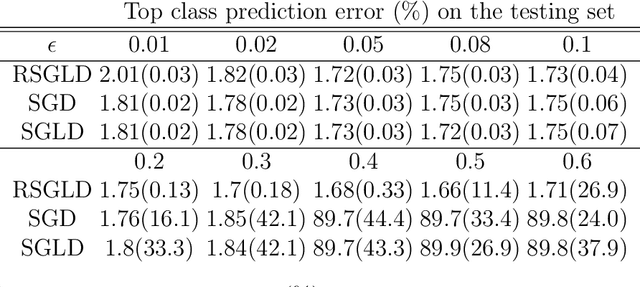
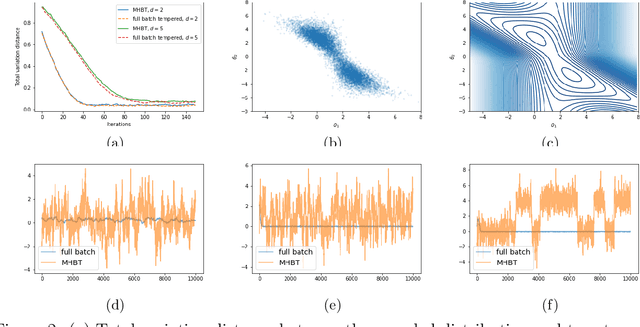
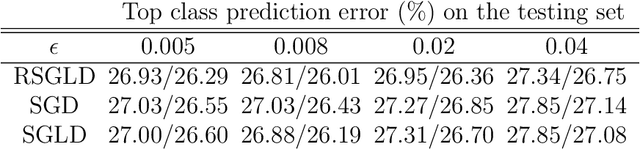
Traditional MCMC algorithms are computationally intensive and do not scale well to large data. In particular, the Metropolis-Hastings (MH) algorithm requires passing over the entire dataset to evaluate the likelihood ratio in each iteration. We propose a general framework for performing MH-MCMC using mini-batches of the whole dataset and show that this gives rise to approximately a tempered stationary distribution. We prove that the algorithm preserves the modes of the original target distribution and derive an error bound on the approximation with mild assumptions on the likelihood. To further extend the utility of the algorithm to high dimensional settings, we construct a proposal with forward and reverse moves using stochastic gradient and show that the construction leads to reasonable acceptance probabilities. We demonstrate the performance of our algorithm in both low dimensional models and high dimensional neural network applications. Particularly in the latter case, compared to popular optimization methods, our method is more robust to the choice of learning rate and improves testing accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge