Adaptive conformal classification with noisy labels

This paper develops novel conformal prediction methods for classification tasks that can automatically adapt to random label contamination in the calibration sample, enabling more informative prediction sets with stronger coverage guarantees compared to state-of-the-art approaches. This is made possible by a precise theoretical characterization of the effective coverage inflation (or deflation) suffered by standard conformal inferences in the presence of label contamination, which is then made actionable through new calibration algorithms. Our solution is flexible and can leverage different modeling assumptions about the label contamination process, while requiring no knowledge about the data distribution or the inner workings of the machine-learning classifier. The advantages of the proposed methods are demonstrated through extensive simulations and an application to object classification with the CIFAR-10H image data set.

Hierarchical Neyman-Pearson Classification for Prioritizing Severe Disease Categories in COVID-19 Patient Data

COVID-19 has a spectrum of disease severity, ranging from asymptomatic to requiring hospitalization. Providing appropriate medical care to severe patients is crucial to reduce mortality risks. Hence, in classifying patients into severity categories, the more important classification errors are "under-diagnosis", in which patients are misclassified into less severe categories and thus receive insufficient medical care. The Neyman-Pearson (NP) classification paradigm has been developed to prioritize the designated type of error. However, current NP procedures are either for binary classification or do not provide high probability controls on the prioritized errors in multi-class classification. Here, we propose a hierarchical NP (H-NP) framework and an umbrella algorithm that generally adapts to popular classification methods and controls the under-diagnosis errors with high probability. On an integrated collection of single-cell RNA-seq (scRNA-seq) datasets for 740 patients, we explore ways of featurization and demonstrate the efficacy of the H-NP algorithm in controlling the under-diagnosis errors regardless of featurization. Beyond COVID-19 severity classification, the H-NP algorithm generally applies to multi-class classification problems, where classes have a priority order.

A Unified Framework for Tuning Hyperparameters in Clustering Problems

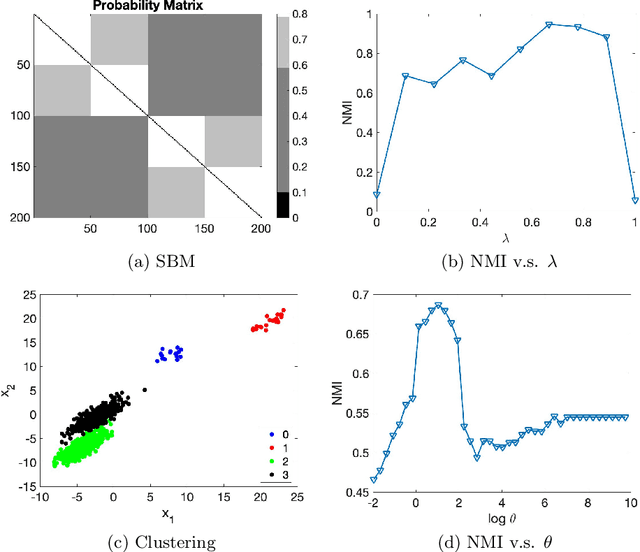
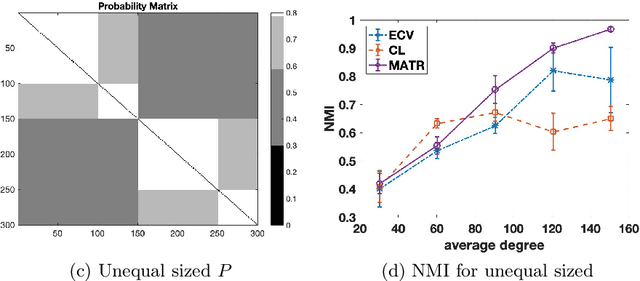
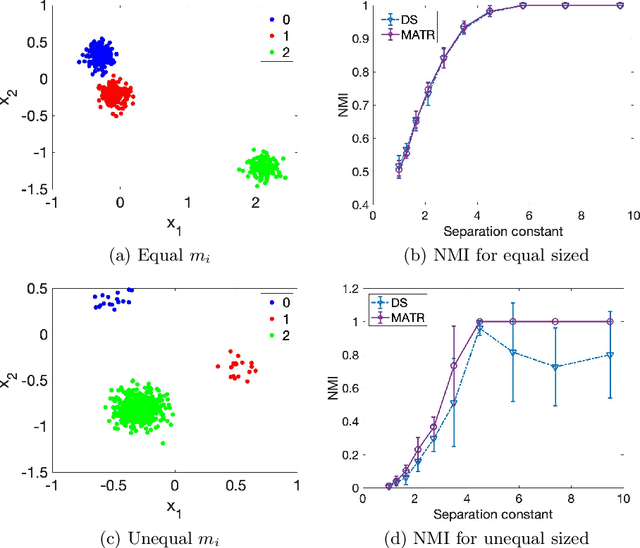
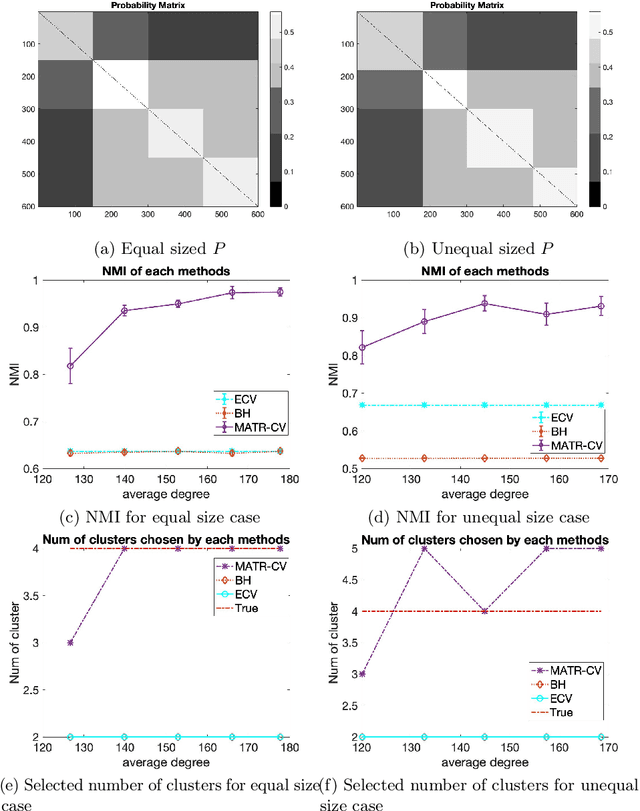
Selecting hyperparameters for unsupervised learning problems is difficult in general due to the lack of ground truth for validation. However, this issue is prevalent in machine learning, especially in clustering problems with examples including the Lagrange multipliers of penalty terms in semidefinite programming (SDP) relaxations and the bandwidths used for constructing kernel similarity matrices for Spectral Clustering. Despite this, there are not many provable algorithms for tuning these hyperparameters. In this paper, we provide a unified framework with provable guarantees for the above class of problems. We demonstrate our method on two distinct models. First, we show how to tune the hyperparameters in widely used SDP algorithms for community detection in networks. In this case, our method can also be used for model selection. Second, we show the same framework works for choosing the bandwidth for the kernel similarity matrix in Spectral Clustering for subgaussian mixtures under suitable model specification. In a variety of simulation experiments, we show that our framework outperforms other widely used tuning procedures in a broad range of parameter settings.

Mini-batch Metropolis-Hastings MCMC with Reversible SGLD Proposal

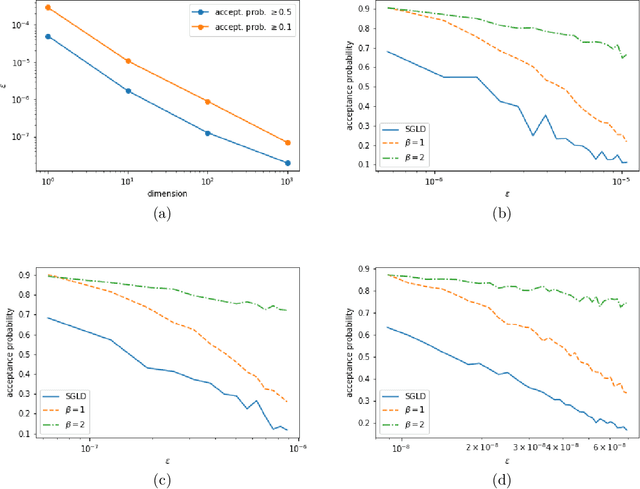
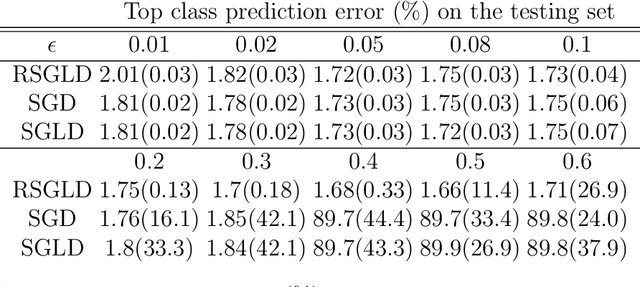
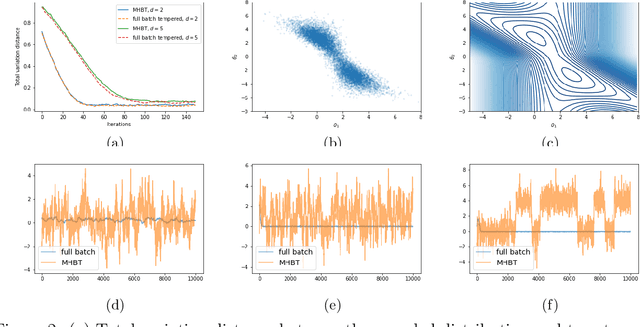
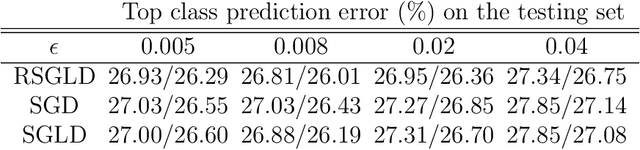
Traditional MCMC algorithms are computationally intensive and do not scale well to large data. In particular, the Metropolis-Hastings (MH) algorithm requires passing over the entire dataset to evaluate the likelihood ratio in each iteration. We propose a general framework for performing MH-MCMC using mini-batches of the whole dataset and show that this gives rise to approximately a tempered stationary distribution. We prove that the algorithm preserves the modes of the original target distribution and derive an error bound on the approximation with mild assumptions on the likelihood. To further extend the utility of the algorithm to high dimensional settings, we construct a proposal with forward and reverse moves using stochastic gradient and show that the construction leads to reasonable acceptance probabilities. We demonstrate the performance of our algorithm in both low dimensional models and high dimensional neural network applications. Particularly in the latter case, compared to popular optimization methods, our method is more robust to the choice of learning rate and improves testing accuracy.