Robust Conformal Outlier Detection under Contaminated Reference Data

Conformal prediction is a flexible framework for calibrating machine learning predictions, providing distribution-free statistical guarantees. In outlier detection, this calibration relies on a reference set of labeled inlier data to control the type-I error rate. However, obtaining a perfectly labeled inlier reference set is often unrealistic, and a more practical scenario involves access to a contaminated reference set containing a small fraction of outliers. This paper analyzes the impact of such contamination on the validity of conformal methods. We prove that under realistic, non-adversarial settings, calibration on contaminated data yields conservative type-I error control, shedding light on the inherent robustness of conformal methods. This conservativeness, however, typically results in a loss of power. To alleviate this limitation, we propose a novel, active data-cleaning framework that leverages a limited labeling budget and an outlier detection model to selectively annotate data points in the contaminated reference set that are suspected as outliers. By removing only the annotated outliers in this ``suspicious'' subset, we can effectively enhance power while mitigating the risk of inflating the type-I error rate, as supported by our theoretical analysis. Experiments on real datasets validate the conservative behavior of conformal methods under contamination and show that the proposed data-cleaning strategy improves power without sacrificing validity.

Noise-Adaptive Conformal Classification with Marginal Coverage

Conformal inference provides a rigorous statistical framework for uncertainty quantification in machine learning, enabling well-calibrated prediction sets with precise coverage guarantees for any classification model. However, its reliance on the idealized assumption of perfect data exchangeability limits its effectiveness in the presence of real-world complications, such as low-quality labels -- a widespread issue in modern large-scale data sets. This work tackles this open problem by introducing an adaptive conformal inference method capable of efficiently handling deviations from exchangeability caused by random label noise, leading to informative prediction sets with tight marginal coverage guarantees even in those challenging scenarios. We validate our method through extensive numerical experiments demonstrating its effectiveness on synthetic and real data sets, including CIFAR-10H and BigEarthNet.

Doubly Robust Conformalized Survival Analysis with Right-Censored Data

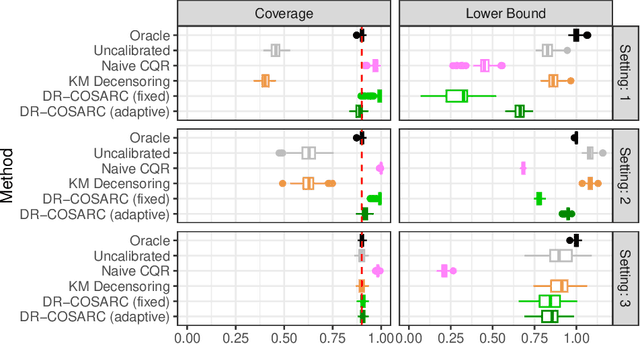
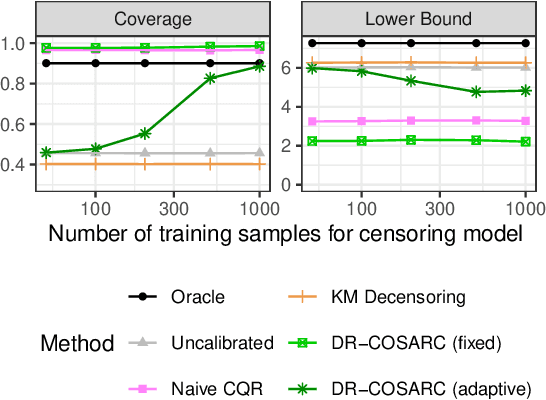
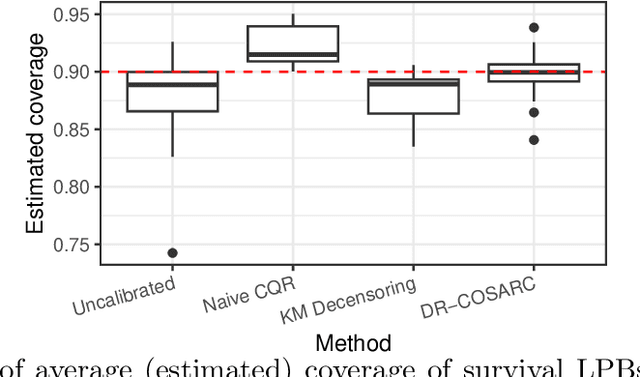
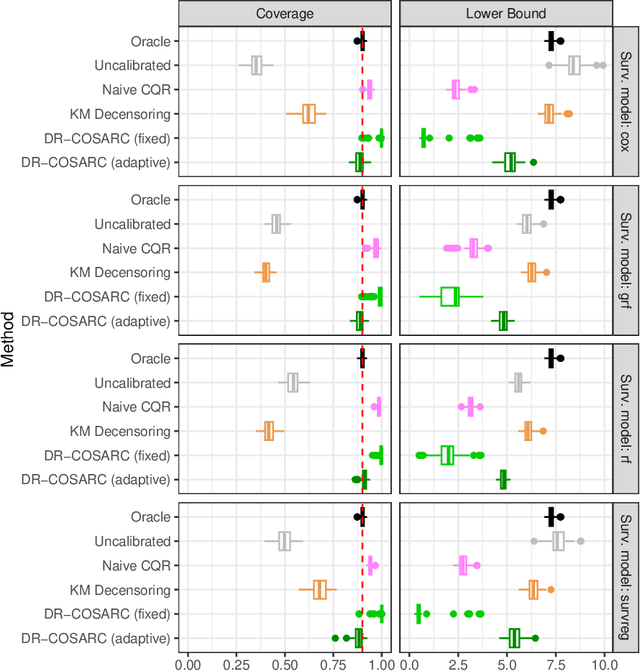
We present a conformal inference method for constructing lower prediction bounds for survival times from right-censored data, extending recent approaches designed for type-I censoring. This method imputes unobserved censoring times using a suitable model, and then analyzes the imputed data using weighted conformal inference. This approach is theoretically supported by an asymptotic double robustness property. Empirical studies on simulated and real data sets demonstrate that our method is more robust than existing approaches in challenging settings where the survival model may be inaccurate, while achieving comparable performance in easier scenarios.

Conformal Classification with Equalized Coverage for Adaptively Selected Groups

This paper introduces a conformal inference method to evaluate uncertainty in classification by generating prediction sets with valid coverage conditional on adaptively chosen features. These features are carefully selected to reflect potential model limitations or biases. This can be useful to find a practical compromise between efficiency -- by providing informative predictions -- and algorithmic fairness -- by ensuring equalized coverage for the most sensitive groups. We demonstrate the validity and effectiveness of this method on simulated and real data sets.

Structured Conformal Inference for Matrix Completion with Applications to Group Recommender Systems

We develop a conformal inference method to construct joint confidence regions for structured groups of missing entries within a sparsely observed matrix. This method is useful to provide reliable uncertainty estimation for group-level collaborative filtering; for example, it can be applied to help suggest a movie for a group of friends to watch together. Unlike standard conformal techniques, which make inferences for one individual at a time, our method achieves stronger group-level guarantees by carefully assembling a structured calibration data set mimicking the patterns expected among the test group of interest. We propose a generalized weighted conformalization framework to deal with the lack of exchangeability arising from such structured calibration, and in this process we introduce several innovations to overcome computational challenges. The practicality and effectiveness of our method are demonstrated through extensive numerical experiments and an analysis of the MovieLens 100K data set.

Uncertainty in Language Models: Assessment through Rank-Calibration

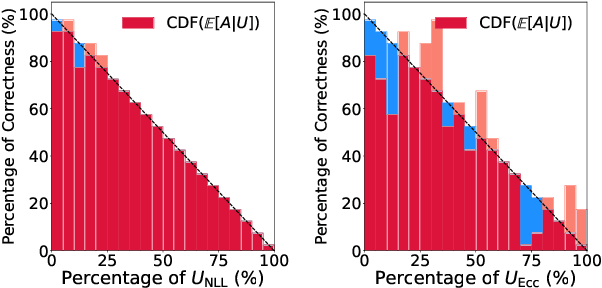
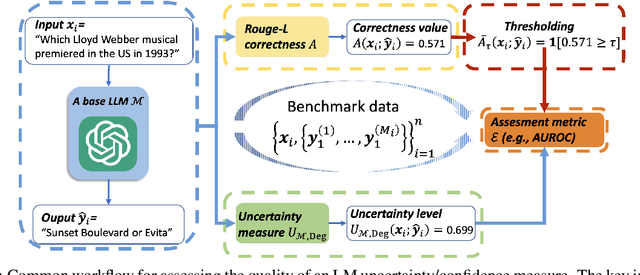
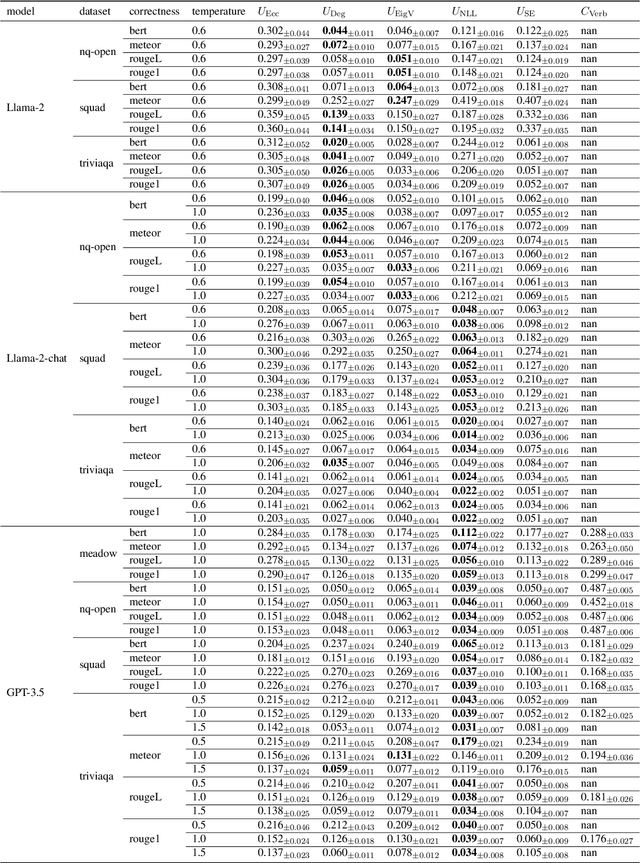
Language Models (LMs) have shown promising performance in natural language generation. However, as LMs often generate incorrect or hallucinated responses, it is crucial to correctly quantify their uncertainty in responding to given inputs. In addition to verbalized confidence elicited via prompting, many uncertainty measures ($e.g.$, semantic entropy and affinity-graph-based measures) have been proposed. However, these measures can differ greatly, and it is unclear how to compare them, partly because they take values over different ranges ($e.g.$, $[0,\infty)$ or $[0,1]$). In this work, we address this issue by developing a novel and practical framework, termed $Rank$-$Calibration$, to assess uncertainty and confidence measures for LMs. Our key tenet is that higher uncertainty (or lower confidence) should imply lower generation quality, on average. Rank-calibration quantifies deviations from this ideal relationship in a principled manner, without requiring ad hoc binary thresholding of the correctness score ($e.g.$, ROUGE or METEOR). The broad applicability and the granular interpretability of our methods are demonstrated empirically.

Conformalized Adaptive Forecasting of Heterogeneous Trajectories

This paper presents a new conformal method for generating simultaneous forecasting bands guaranteed to cover the entire path of a new random trajectory with sufficiently high probability. Prompted by the need for dependable uncertainty estimates in motion planning applications where the behavior of diverse objects may be more or less unpredictable, we blend different techniques from online conformal prediction of single and multiple time series, as well as ideas for addressing heteroscedasticity in regression. This solution is both principled, providing precise finite-sample guarantees, and effective, often leading to more informative predictions than prior methods.

Frequency and cardinality recovery from sketched data: a novel approach bridging Bayesian and frequentist views

We study how to recover the frequency of a symbol in a large discrete data set, using only a compressed representation, or sketch, of those data obtained via random hashing. This is a classical problem in computer science, with various algorithms available, such as the count-min sketch. However, these algorithms often assume that the data are fixed, leading to overly conservative and potentially inaccurate estimates when dealing with randomly sampled data. In this paper, we consider the sketched data as a random sample from an unknown distribution, and then we introduce novel estimators that improve upon existing approaches. Our method combines Bayesian nonparametric and classical (frequentist) perspectives, addressing their unique limitations to provide a principled and practical solution. Additionally, we extend our method to address the related but distinct problem of cardinality recovery, which consists of estimating the total number of distinct objects in the data set. We validate our method on synthetic and real data, comparing its performance to state-of-the-art alternatives.

Adaptive conformal classification with noisy labels

This paper develops novel conformal prediction methods for classification tasks that can automatically adapt to random label contamination in the calibration sample, enabling more informative prediction sets with stronger coverage guarantees compared to state-of-the-art approaches. This is made possible by a precise theoretical characterization of the effective coverage inflation (or deflation) suffered by standard conformal inferences in the presence of label contamination, which is then made actionable through new calibration algorithms. Our solution is flexible and can leverage different modeling assumptions about the label contamination process, while requiring no knowledge about the data distribution or the inner workings of the machine-learning classifier. The advantages of the proposed methods are demonstrated through extensive simulations and an application to object classification with the CIFAR-10H image data set.

Derandomized Novelty Detection with FDR Control via Conformal E-values

Conformal prediction and other randomized model-free inference techniques are gaining increasing attention as general solutions to rigorously calibrate the output of any machine learning algorithm for novelty detection. This paper contributes to the field by developing a novel method for mitigating their algorithmic randomness, leading to an even more interpretable and reliable framework for powerful novelty detection under false discovery rate control. The idea is to leverage suitable conformal e-values instead of p-values to quantify the significance of each finding, which allows the evidence gathered from multiple mutually dependent analyses of the same data to be seamlessly aggregated. Further, the proposed method can reduce randomness without much loss of power, partly thanks to an innovative way of weighting conformal e-values based on additional side information carefully extracted from the same data. Simulations with synthetic and real data confirm this solution can be effective at eliminating random noise in the inferences obtained with state-of-the-art alternative techniques, sometimes also leading to higher power.