Robust Conformal Outlier Detection under Contaminated Reference Data

Conformal prediction is a flexible framework for calibrating machine learning predictions, providing distribution-free statistical guarantees. In outlier detection, this calibration relies on a reference set of labeled inlier data to control the type-I error rate. However, obtaining a perfectly labeled inlier reference set is often unrealistic, and a more practical scenario involves access to a contaminated reference set containing a small fraction of outliers. This paper analyzes the impact of such contamination on the validity of conformal methods. We prove that under realistic, non-adversarial settings, calibration on contaminated data yields conservative type-I error control, shedding light on the inherent robustness of conformal methods. This conservativeness, however, typically results in a loss of power. To alleviate this limitation, we propose a novel, active data-cleaning framework that leverages a limited labeling budget and an outlier detection model to selectively annotate data points in the contaminated reference set that are suspected as outliers. By removing only the annotated outliers in this ``suspicious'' subset, we can effectively enhance power while mitigating the risk of inflating the type-I error rate, as supported by our theoretical analysis. Experiments on real datasets validate the conservative behavior of conformal methods under contamination and show that the proposed data-cleaning strategy improves power without sacrificing validity.

Segment-Based Attention Masking for GPTs

Modern Language Models (LMs) owe much of their success to masked causal attention, the backbone of Generative Pre-Trained Transformer (GPT) models. Although GPTs can process the entire user prompt at once, the causal masking is applied to all input tokens step-by-step, mimicking the generation process. This imposes an unnecessary constraint during the initial "prefill" phase when the model processes the input prompt and generates the internal representations before producing any output tokens. In this work, attention is masked based on the known block structure at the prefill phase, followed by the conventional token-by-token autoregressive process after that. For example, in a typical chat prompt, the system prompt is treated as one block, and the user prompt as the next one. Each of these is treated as a unit for the purpose of masking, such that the first tokens in each block can access the subsequent tokens in a non-causal manner. Then, the model answer is generated in the conventional causal manner. This Segment-by-Segment scheme entails no additional computational overhead. When integrating it into models such as Llama and Qwen, state-of-the-art performance is consistently achieved.

Semi-Supervised Risk Control via Prediction-Powered Inference

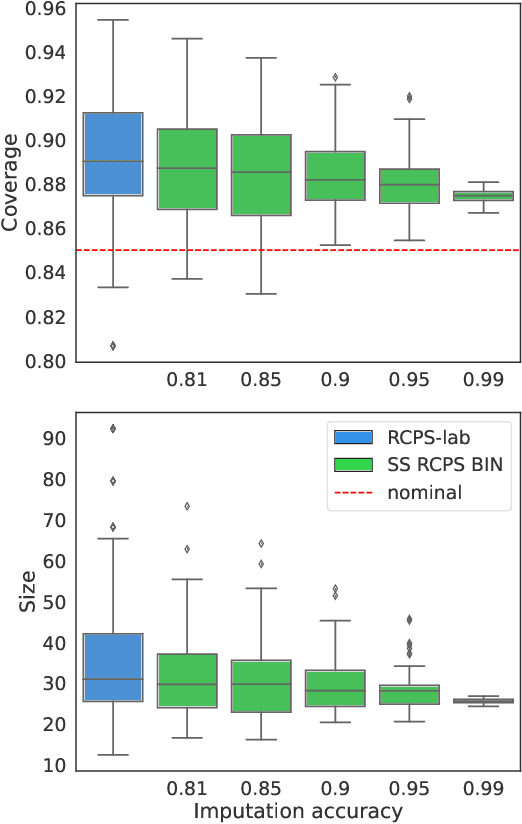
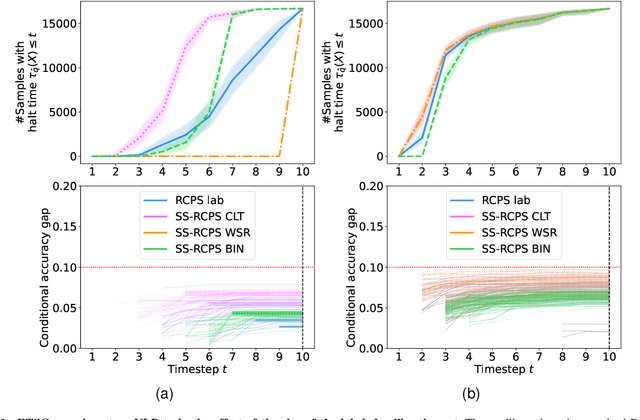
The risk-controlling prediction sets (RCPS) framework is a general tool for transforming the output of any machine learning model to design a predictive rule with rigorous error rate control. The key idea behind this framework is to use labeled hold-out calibration data to tune a hyper-parameter that affects the error rate of the resulting prediction rule. However, the limitation of such a calibration scheme is that with limited hold-out data, the tuned hyper-parameter becomes noisy and leads to a prediction rule with an error rate that is often unnecessarily conservative. To overcome this sample-size barrier, we introduce a semi-supervised calibration procedure that leverages unlabeled data to rigorously tune the hyper-parameter without compromising statistical validity. Our procedure builds upon the prediction-powered inference framework, carefully tailoring it to risk-controlling tasks. We demonstrate the benefits and validity of our proposal through two real-data experiments: few-shot image classification and early time series classification.

Protected Test-Time Adaptation via Online Entropy Matching: A Betting Approach

We present a novel approach for test-time adaptation via online self-training, consisting of two components. First, we introduce a statistical framework that detects distribution shifts in the classifier's entropy values obtained on a stream of unlabeled samples. Second, we devise an online adaptation mechanism that utilizes the evidence of distribution shifts captured by the detection tool to dynamically update the classifier's parameters. The resulting adaptation process drives the distribution of test entropy values obtained from the self-trained classifier to match those of the source domain, building invariance to distribution shifts. This approach departs from the conventional self-training method, which focuses on minimizing the classifier's entropy. Our approach combines concepts in betting martingales and online learning to form a detection tool capable of quickly reacting to distribution shifts. We then reveal a tight relation between our adaptation scheme and optimal transport, which forms the basis of our novel self-supervised loss. Experimental results demonstrate that our approach improves test-time accuracy under distribution shifts while maintaining accuracy and calibration in their absence, outperforming leading entropy minimization methods across various scenarios.

Pivotal Auto-Encoder via Self-Normalizing ReLU

Sparse auto-encoders are useful for extracting low-dimensional representations from high-dimensional data. However, their performance degrades sharply when the input noise at test time differs from the noise employed during training. This limitation hinders the applicability of auto-encoders in real-world scenarios where the level of noise in the input is unpredictable. In this paper, we formalize single hidden layer sparse auto-encoders as a transform learning problem. Leveraging the transform modeling interpretation, we propose an optimization problem that leads to a predictive model invariant to the noise level at test time. In other words, the same pre-trained model is able to generalize to different noise levels. The proposed optimization algorithm, derived from the square root lasso, is translated into a new, computationally efficient auto-encoding architecture. After proving that our new method is invariant to the noise level, we evaluate our approach by training networks using the proposed architecture for denoising tasks. Our experimental results demonstrate that the trained models yield a significant improvement in stability against varying types of noise compared to commonly used architectures.

Robust Conformal Prediction Using Privileged Information

We develop a method to generate prediction sets with a guaranteed coverage rate that is robust to corruptions in the training data, such as missing or noisy variables. Our approach builds on conformal prediction, a powerful framework to construct prediction sets that are valid under the i.i.d assumption. Importantly, naively applying conformal prediction does not provide reliable predictions in this setting, due to the distribution shift induced by the corruptions. To account for the distribution shift, we assume access to privileged information (PI). The PI is formulated as additional features that explain the distribution shift, however, they are only available during training and absent at test time. We approach this problem by introducing a novel generalization of weighted conformal prediction and support our method with theoretical coverage guarantees. Empirical experiments on both real and synthetic datasets indicate that our approach achieves a valid coverage rate and constructs more informative predictions compared to existing methods, which are not supported by theoretical guarantees.

Strategy-Proof Auctions through Conformal Prediction

Auctions are key for maximizing sellers' revenue and ensuring truthful bidding among buyers. Recently, an approach known as differentiable economics based on deep learning shows promise in learning optimal auction mechanisms for multiple items and participants. However, this approach has no guarantee of strategy-proofness at test time. Strategy-proofness is crucial as it ensures that buyers are incentivized to bid their true valuations, leading to optimal and fair auction outcomes without the risk of manipulation. Building on conformal prediction, we introduce a novel approach to achieve strategy-proofness with rigorous statistical guarantees. The key novelties of our method are: (i) the formulation of a regret prediction model, used to quantify at test time violations of strategy-proofness; and (ii) an auction acceptance rule that leverages the predicted regret to ensure that for a new auction, the data-driven mechanism meets the strategy-proofness requirement with high probability (e.g., 99\%). Numerical experiments demonstrate the necessity for rigorous guarantees, the validity of our theoretical results, and the applicability of our proposed method.

Provably Robust Conformal Prediction with Improved Efficiency

Conformal prediction is a powerful tool to generate uncertainty sets with guaranteed coverage using any predictive model, under the assumption that the training and test data are i.i.d.. Recently, it has been shown that adversarial examples are able to manipulate conformal methods to construct prediction sets with invalid coverage rates, as the i.i.d. assumption is violated. To address this issue, a recent work, Randomized Smoothed Conformal Prediction (RSCP), was first proposed to certify the robustness of conformal prediction methods to adversarial noise. However, RSCP has two major limitations: (i) its robustness guarantee is flawed when used in practice and (ii) it tends to produce large uncertainty sets. To address these limitations, we first propose a novel framework called RSCP+ to provide provable robustness guarantee in evaluation, which fixes the issues in the original RSCP method. Next, we propose two novel methods, Post-Training Transformation (PTT) and Robust Conformal Training (RCT), to effectively reduce prediction set size with little computation overhead. Experimental results in CIFAR10, CIFAR100, and ImageNet suggest the baseline method only yields trivial predictions including full label set, while our methods could boost the efficiency by up to $4.36\times$, $5.46\times$, and $16.9\times$ respectively and provide practical robustness guarantee. Our codes are available at https://github.com/Trustworthy-ML-Lab/Provably-Robust-Conformal-Prediction.

Early Time Classification with Accumulated Accuracy Gap Control

Early time classification algorithms aim to label a stream of features without processing the full input stream, while maintaining accuracy comparable to that achieved by applying the classifier to the entire input. In this paper, we introduce a statistical framework that can be applied to any sequential classifier, formulating a calibrated stopping rule. This data-driven rule attains finite-sample, distribution-free control of the accuracy gap between full and early-time classification. We start by presenting a novel method that builds on the Learn-then-Test calibration framework to control this gap marginally, on average over i.i.d. instances. As this algorithm tends to yield an excessively high accuracy gap for early halt times, our main contribution is the proposal of a framework that controls a stronger notion of error, where the accuracy gap is controlled conditionally on the accumulated halt times. Numerical experiments demonstrate the effectiveness, applicability, and usefulness of our method. We show that our proposed early stopping mechanism reduces up to 94% of timesteps used for classification while achieving rigorous accuracy gap control.

Conformal Prediction with Missing Values

Conformal prediction is a theoretically grounded framework for constructing predictive intervals. We study conformal prediction with missing values in the covariates -- a setting that brings new challenges to uncertainty quantification. We first show that the marginal coverage guarantee of conformal prediction holds on imputed data for any missingness distribution and almost all imputation functions. However, we emphasize that the average coverage varies depending on the pattern of missing values: conformal methods tend to construct prediction intervals that under-cover the response conditionally to some missing patterns. This motivates our novel generalized conformalized quantile regression framework, missing data augmentation, which yields prediction intervals that are valid conditionally to the patterns of missing values, despite their exponential number. We then show that a universally consistent quantile regression algorithm trained on the imputed data is Bayes optimal for the pinball risk, thus achieving valid coverage conditionally to any given data point. Moreover, we examine the case of a linear model, which demonstrates the importance of our proposal in overcoming the heteroskedasticity induced by missing values. Using synthetic and data from critical care, we corroborate our theory and report improved performance of our methods.