Learning a Continue-Thinking Token for Enhanced Test-Time Scaling

Test-time scaling has emerged as an effective approach for improving language model performance by utilizing additional compute at inference time. Recent studies have shown that overriding end-of-thinking tokens (e.g., replacing "</think>" with "Wait") can extend reasoning steps and improve accuracy. In this work, we explore whether a dedicated continue-thinking token can be learned to trigger extended reasoning. We augment a distilled version of DeepSeek-R1 with a single learned "<|continue-thinking|>" token, training only its embedding via reinforcement learning while keeping the model weights frozen. Our experiments show that this learned token achieves improved accuracy on standard math benchmarks compared to both the baseline model and a test-time scaling approach that uses a fixed token (e.g., "Wait") for budget forcing. In particular, we observe that in cases where the fixed-token approach enhances the base model's accuracy, our method achieves a markedly greater improvement. For example, on the GSM8K benchmark, the fixed-token approach yields a 1.3% absolute improvement in accuracy, whereas our learned-token method achieves a 4.2% improvement over the base model that does not use budget forcing.

Generic Coreset for Scalable Learning of Monotonic Kernels: Logistic Regression, Sigmoid and more

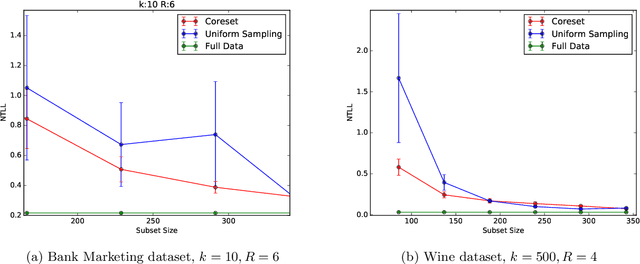
Coreset (or core-set) in this paper is a small weighted \emph{subset} $Q$ of the input set $P$ with respect to a given \emph{monotonic} function $\phi:\REAL\to\REAL$ that \emph{provably} approximates its fitting loss $\sum_{p\in P}f(p\cdot x)$ to \emph{any} given $x\in\REAL^d$. Using $Q$ we can obtain approximation of $x^*$ that minimizes this loss, by running \emph{existing} optimization algorithms on $Q$. We provide: (I) a lower bound that proves that there are sets with no coresets smaller than $n=|P|$ , (II) a proof that a small coreset of size near-logarithmic in $n$ exists for \emph{any} input $P$, under natural assumption that holds e.g. for logistic regression and the sigmoid activation function. (III) a generic algorithm that computes $Q$ in $O(nd+n\log n)$ expected time, (IV) extensive experimental results with open code and benchmarks that show that the coresets are even smaller in practice. Existing papers (e.g.[Huggins,Campbell,Broderick 2016]) suggested only specific coresets for specific input sets.

The UN Parallel Corpus Annotated for Translation Direction

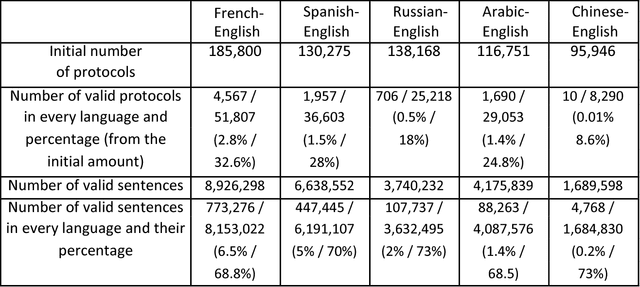
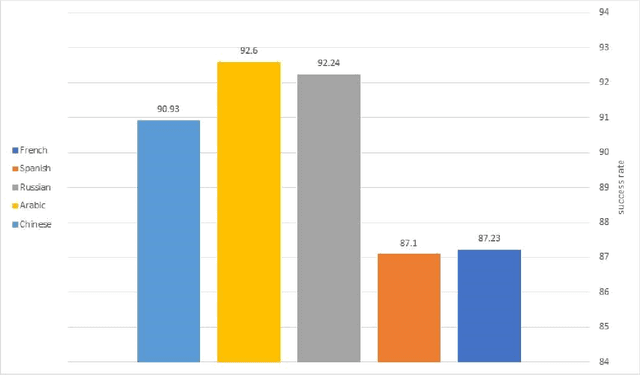
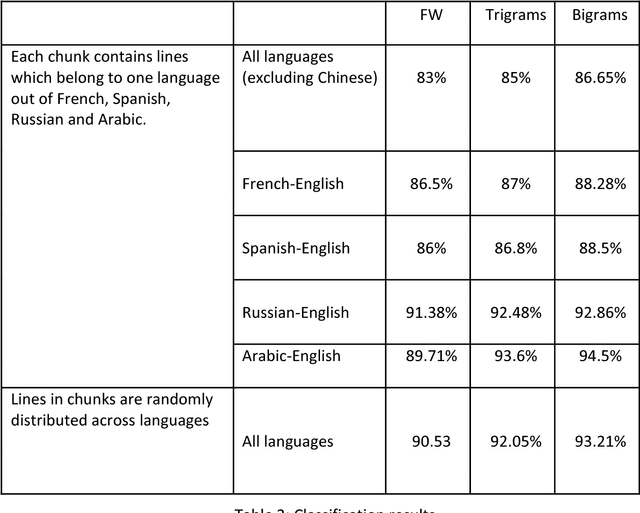
This work distinguishes between translated and original text in the UN protocol corpus. By modeling the problem as classification problem, we can achieve up to 95% classification accuracy. We begin by deriving a parallel corpus for different language-pairs annotated for translation direction, and then classify the data by using various feature extraction methods. We compare the different methods as well as the ability to distinguish between translated and original texts in the different languages. The annotated corpus is publicly available.