Generic Coreset for Scalable Learning of Monotonic Kernels: Logistic Regression, Sigmoid and more
Paper and Code
Jun 10, 2018
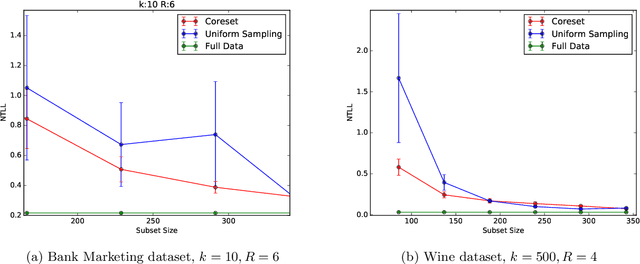
Coreset (or core-set) in this paper is a small weighted \emph{subset} $Q$ of the input set $P$ with respect to a given \emph{monotonic} function $\phi:\REAL\to\REAL$ that \emph{provably} approximates its fitting loss $\sum_{p\in P}f(p\cdot x)$ to \emph{any} given $x\in\REAL^d$. Using $Q$ we can obtain approximation of $x^*$ that minimizes this loss, by running \emph{existing} optimization algorithms on $Q$. We provide: (I) a lower bound that proves that there are sets with no coresets smaller than $n=|P|$ , (II) a proof that a small coreset of size near-logarithmic in $n$ exists for \emph{any} input $P$, under natural assumption that holds e.g. for logistic regression and the sigmoid activation function. (III) a generic algorithm that computes $Q$ in $O(nd+n\log n)$ expected time, (IV) extensive experimental results with open code and benchmarks that show that the coresets are even smaller in practice. Existing papers (e.g.[Huggins,Campbell,Broderick 2016]) suggested only specific coresets for specific input sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge