Dynamic Byzantine-Robust Learning: Adapting to Switching Byzantine Workers

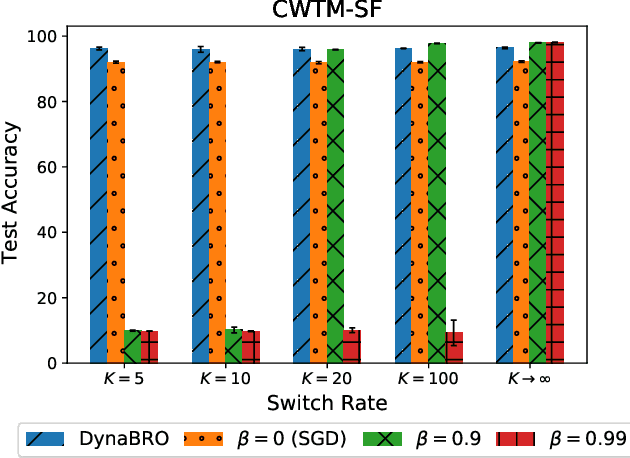
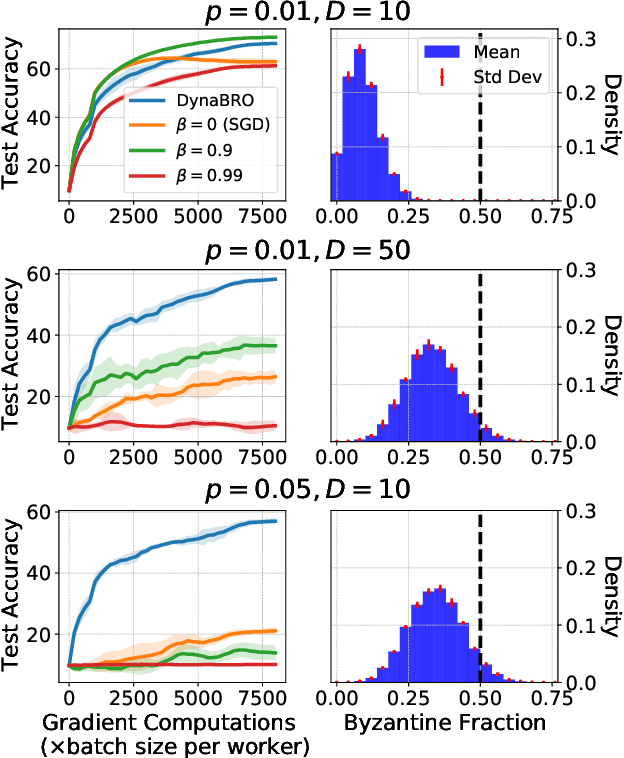
Byzantine-robust learning has emerged as a prominent fault-tolerant distributed machine learning framework. However, most techniques consider the static setting, wherein the identity of Byzantine machines remains fixed during the learning process. This assumption does not capture real-world dynamic Byzantine behaviors, which may include transient malfunctions or targeted temporal attacks. Addressing this limitation, we propose $\textsf{DynaBRO}$ -- a new method capable of withstanding $\mathcal{O}(\sqrt{T})$ rounds of Byzantine identity alterations (where $T$ is the total number of training rounds), while matching the asymptotic convergence rate of the static setting. Our method combines a multi-level Monte Carlo (MLMC) gradient estimation technique with robust aggregation of worker updates and incorporates a fail-safe filter to limit bias from dynamic Byzantine strategies. Additionally, by leveraging an adaptive learning rate, our approach eliminates the need for knowing the percentage of Byzantine workers.

$\texttt{DoCoFL}$: Downlink Compression for Cross-Device Federated Learning

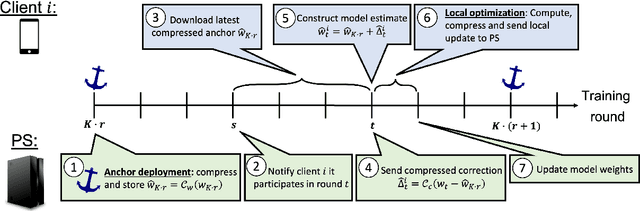
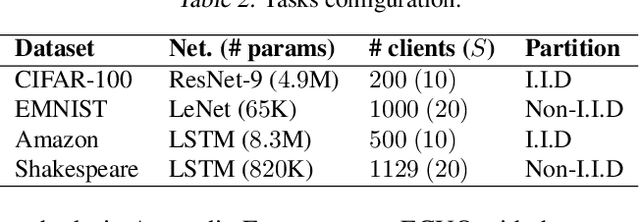
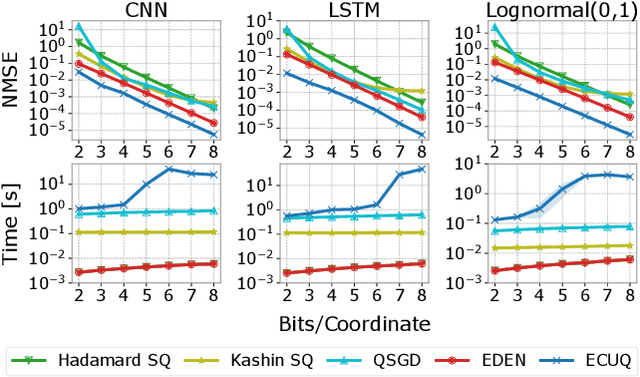
Many compression techniques have been proposed to reduce the communication overhead of Federated Learning training procedures. However, these are typically designed for compressing model updates, which are expected to decay throughout training. As a result, such methods are inapplicable to downlink (i.e., from the parameter server to clients) compression in the cross-device setting, where heterogeneous clients $\textit{may appear only once}$ during training and thus must download the model parameters. In this paper, we propose a new framework ($\texttt{DoCoFL}$) for downlink compression in the cross-device federated learning setting. Importantly, $\texttt{DoCoFL}$ can be seamlessly combined with many uplink compression schemes, rendering it suitable for bi-directional compression. Through extensive evaluation, we demonstrate that $\texttt{DoCoFL}$ offers significant bi-directional bandwidth reduction while achieving competitive accuracy to that of $\texttt{FedAvg}$ without compression.

Adapting to Mixing Time in Stochastic Optimization with Markovian Data

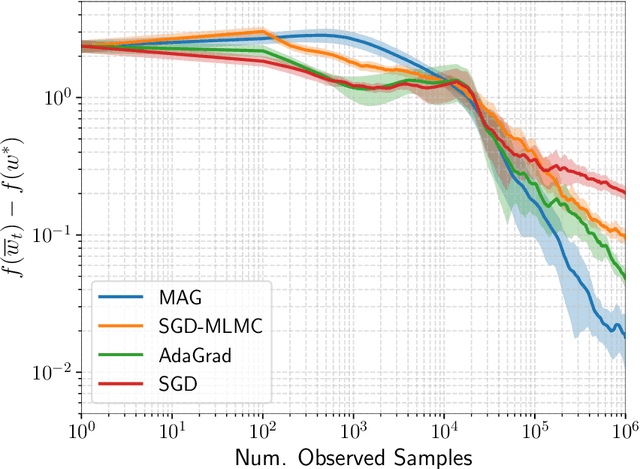
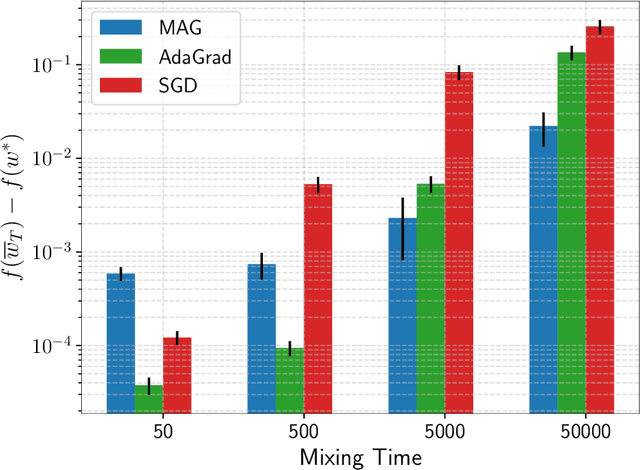
We consider stochastic optimization problems where data is drawn from a Markov chain. Existing methods for this setting crucially rely on knowing the mixing time of the chain, which in real-world applications is usually unknown. We propose the first optimization method that does not require the knowledge of the mixing time, yet obtains the optimal asymptotic convergence rate when applied to convex problems. We further show that our approach can be extended to: (i) finding stationary points in non-convex optimization with Markovian data, and (ii) obtaining better dependence on the mixing time in temporal difference (TD) learning; in both cases, our method is completely oblivious to the mixing time. Our method relies on a novel combination of multi-level Monte Carlo (MLMC) gradient estimation together with an adaptive learning method.

Offline Meta Reinforcement Learning

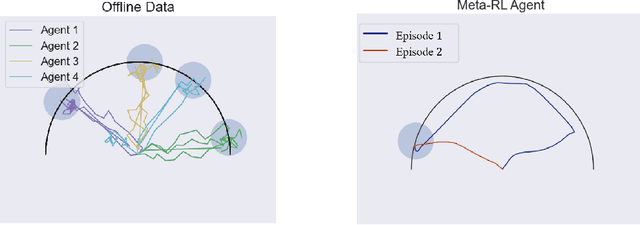
Consider the following problem, which we term Offline Meta Reinforcement Learning (OMRL): given the complete training histories of $N$ conventional RL agents, trained on $N$ different tasks, design a learning agent that can quickly maximize reward in a new, unseen task from the same task distribution. In particular, while each conventional RL agent explored and exploited its own different task, the OMRL agent must identify regularities in the data that lead to effective exploration/exploitation in the unseen task. To solve OMRL, we take a Bayesian RL (BRL) view, and seek to learn a Bayes-optimal policy from the offline data. We extend the recently proposed VariBAD BRL algorithm to the off-policy setting, and demonstrate learning of Bayes-optimal exploration strategies from offline data using deep neural networks. Furthermore, when applied to the online meta-RL setting (agent simultaneously collects data and improves its meta-RL policy), our method is significantly more sample efficient than the conventional VariBAD.