Safety in the Face of Adversity: Achieving Zero Constraint Violation in Online Learning with Slowly Changing Constraints

We present the first theoretical guarantees for zero constraint violation in Online Convex Optimization (OCO) across all rounds, addressing dynamic constraint changes. Unlike existing approaches in constrained OCO, which allow for occasional safety breaches, we provide the first approach for maintaining strict safety under the assumption of gradually evolving constraints, namely the constraints change at most by a small amount between consecutive rounds. This is achieved through a primal-dual approach and Online Gradient Ascent in the dual space. We show that employing a dichotomous learning rate enables ensuring both safety, via zero constraint violation, and sublinear regret. Our framework marks a departure from previous work by providing the first provable guarantees for maintaining absolute safety in the face of changing constraints in OCO.

DE-PADA: Personalized Augmentation and Domain Adaptation for ECG Biometrics Across Physiological States

Electrocardiogram (ECG)-based biometrics offer a promising method for user identification, combining intrinsic liveness detection with morphological uniqueness. However, elevated heart rates introduce significant physiological variability, posing challenges to pattern recognition systems and leading to a notable performance gap between resting and post-exercise conditions. Addressing this gap is critical for advancing ECG-based biometric systems for real-world applications. We propose DE-PADA, a Dual Expert model with Personalized Augmentation and Domain Adaptation, designed to enhance robustness across diverse physiological states. The model is trained primarily on resting-state data from the evaluation dataset, without direct exposure to their exercise data. To address variability, DE-PADA incorporates ECG-specific innovations, including heartbeat segmentation into the PQRS interval, known for its relative temporal consistency, and the heart rate-sensitive ST interval, enabling targeted feature extraction tailored to each region's unique characteristics. Personalized augmentation simulates subject-specific T-wave variability across heart rates using individual T-wave peak predictions to adapt augmentation ranges. Domain adaptation further improves generalization by leveraging auxiliary data from supplementary subjects used exclusively for training, including both resting and exercise conditions. Experiments on the University of Toronto ECG Database demonstrate the model's effectiveness. DE-PADA achieves relative improvements in post-exercise identification rates of 26.75% in the initial recovery phase and 11.72% in the late recovery phase, while maintaining a 98.12% identification rate in the sitting position. These results highlight DE-PADA's ability to address intra-subject variability and enhance the robustness of ECG-based biometric systems across diverse physiological states.

Weight for Robustness: A Comprehensive Approach towards Optimal Fault-Tolerant Asynchronous ML

We address the challenges of Byzantine-robust training in asynchronous distributed machine learning systems, aiming to enhance efficiency amid massive parallelization and heterogeneous computing resources. Asynchronous systems, marked by independently operating workers and intermittent updates, uniquely struggle with maintaining integrity against Byzantine failures, which encompass malicious or erroneous actions that disrupt learning. The inherent delays in such settings not only introduce additional bias to the system but also obscure the disruptions caused by Byzantine faults. To tackle these issues, we adapt the Byzantine framework to asynchronous dynamics by introducing a novel weighted robust aggregation framework. This allows for the extension of robust aggregators and a recent meta-aggregator to their weighted versions, mitigating the effects of delayed updates. By further incorporating a recent variance-reduction technique, we achieve an optimal convergence rate for the first time in an asynchronous Byzantine environment. Our methodology is rigorously validated through empirical and theoretical analysis, demonstrating its effectiveness in enhancing fault tolerance and optimizing performance in asynchronous ML systems.

Private and Federated Stochastic Convex Optimization: Efficient Strategies for Centralized Systems

This paper addresses the challenge of preserving privacy in Federated Learning (FL) within centralized systems, focusing on both trusted and untrusted server scenarios. We analyze this setting within the Stochastic Convex Optimization (SCO) framework, and devise methods that ensure Differential Privacy (DP) while maintaining optimal convergence rates for homogeneous and heterogeneous data distributions. Our approach, based on a recent stochastic optimization technique, offers linear computational complexity, comparable to non-private FL methods, and reduced gradient obfuscation. This work enhances the practicality of DP in FL, balancing privacy, efficiency, and robustness in a variety of server trust environment.

Fault Tolerant ML: Efficient Meta-Aggregation and Synchronous Training

In this paper, we investigate the challenging framework of Byzantine-robust training in distributed machine learning (ML) systems, focusing on enhancing both efficiency and practicality. As distributed ML systems become integral for complex ML tasks, ensuring resilience against Byzantine failures-where workers may contribute incorrect updates due to malice or error-gains paramount importance. Our first contribution is the introduction of the Centered Trimmed Meta Aggregator (CTMA), an efficient meta-aggregator that upgrades baseline aggregators to optimal performance levels, while requiring low computational demands. Additionally, we propose harnessing a recently developed gradient estimation technique based on a double-momentum strategy within the Byzantine context. Our paper highlights its theoretical and practical advantages for Byzantine-robust training, especially in simplifying the tuning process and reducing the reliance on numerous hyperparameters. The effectiveness of this technique is supported by theoretical insights within the stochastic convex optimization (SCO) framework.

On the Global Convergence of Policy Gradient in Average Reward Markov Decision Processes

We present the first finite time global convergence analysis of policy gradient in the context of infinite horizon average reward Markov decision processes (MDPs). Specifically, we focus on ergodic tabular MDPs with finite state and action spaces. Our analysis shows that the policy gradient iterates converge to the optimal policy at a sublinear rate of $O\left({\frac{1}{T}}\right),$ which translates to $O\left({\log(T)}\right)$ regret, where $T$ represents the number of iterations. Prior work on performance bounds for discounted reward MDPs cannot be extended to average reward MDPs because the bounds grow proportional to the fifth power of the effective horizon. Thus, our primary contribution is in proving that the policy gradient algorithm converges for average-reward MDPs and in obtaining finite-time performance guarantees. In contrast to the existing discounted reward performance bounds, our performance bounds have an explicit dependence on constants that capture the complexity of the underlying MDP. Motivated by this observation, we reexamine and improve the existing performance bounds for discounted reward MDPs. We also present simulations to empirically evaluate the performance of average reward policy gradient algorithm.

Dynamic Byzantine-Robust Learning: Adapting to Switching Byzantine Workers

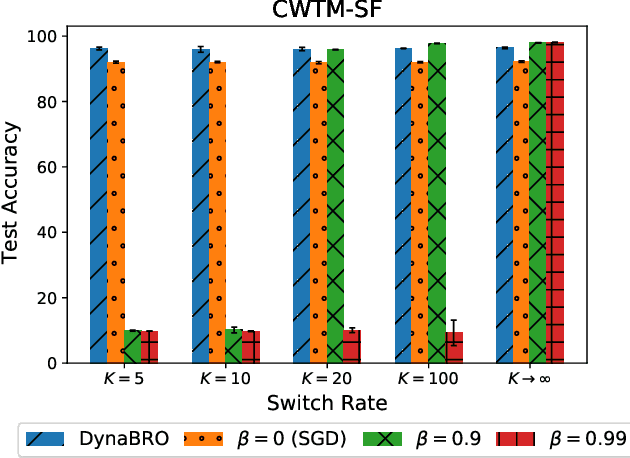
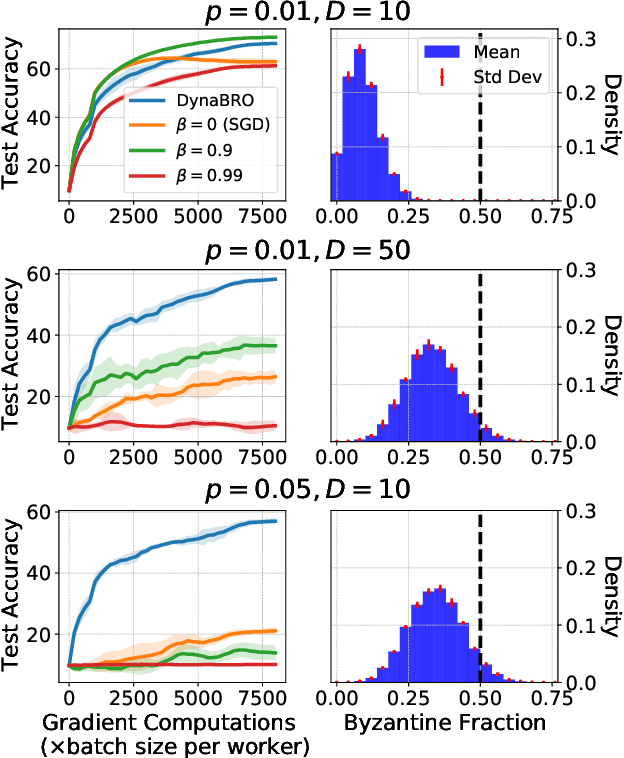
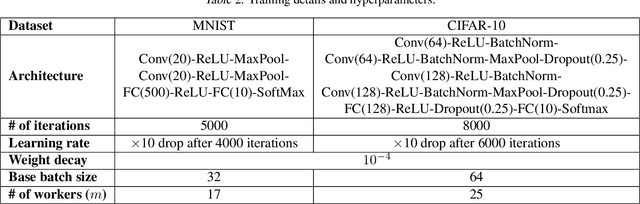
Byzantine-robust learning has emerged as a prominent fault-tolerant distributed machine learning framework. However, most techniques consider the static setting, wherein the identity of Byzantine machines remains fixed during the learning process. This assumption does not capture real-world dynamic Byzantine behaviors, which may include transient malfunctions or targeted temporal attacks. Addressing this limitation, we propose $\textsf{DynaBRO}$ -- a new method capable of withstanding $\mathcal{O}(\sqrt{T})$ rounds of Byzantine identity alterations (where $T$ is the total number of training rounds), while matching the asymptotic convergence rate of the static setting. Our method combines a multi-level Monte Carlo (MLMC) gradient estimation technique with robust aggregation of worker updates and incorporates a fail-safe filter to limit bias from dynamic Byzantine strategies. Additionally, by leveraging an adaptive learning rate, our approach eliminates the need for knowing the percentage of Byzantine workers.

Meta-Learning Adversarial Bandit Algorithms

We study online meta-learning with bandit feedback, with the goal of improving performance across multiple tasks if they are similar according to some natural similarity measure. As the first to target the adversarial online-within-online partial-information setting, we design meta-algorithms that combine outer learners to simultaneously tune the initialization and other hyperparameters of an inner learner for two important cases: multi-armed bandits (MAB) and bandit linear optimization (BLO). For MAB, the meta-learners initialize and set hyperparameters of the Tsallis-entropy generalization of Exp3, with the task-averaged regret improving if the entropy of the optima-in-hindsight is small. For BLO, we learn to initialize and tune online mirror descent (OMD) with self-concordant barrier regularizers, showing that task-averaged regret varies directly with an action space-dependent measure they induce. Our guarantees rely on proving that unregularized follow-the-leader combined with two levels of low-dimensional hyperparameter tuning is enough to learn a sequence of affine functions of non-Lipschitz and sometimes non-convex Bregman divergences bounding the regret of OMD.

SLowcal-SGD: Slow Query Points Improve Local-SGD for Stochastic Convex Optimization

We consider distributed learning scenarios where M machines interact with a parameter server along several communication rounds in order to minimize a joint objective function. Focusing on the heterogeneous case, where different machines may draw samples from different data-distributions, we design the first local update method that provably benefits over the two most prominent distributed baselines: namely Minibatch-SGD and Local-SGD. Key to our approach is a slow querying technique that we customize to the distributed setting, which in turn enables a better mitigation of the bias caused by local updates.

$μ^2$-SGD: Stable Stochastic Optimization via a Double Momentum Mechanism

We consider stochastic convex optimization problems where the objective is an expectation over smooth functions. For this setting we suggest a novel gradient estimate that combines two recent mechanism that are related to notion of momentum. Then, we design an SGD-style algorithm as well as an accelerated version that make use of this new estimator, and demonstrate the robustness of these new approaches to the choice of the learning rate. Concretely, we show that these approaches obtain the optimal convergence rates for both noiseless and noisy case with the same choice of fixed learning rate. Moreover, for the noisy case we show that these approaches achieve the same optimal bound for a very wide range of learning rates.