Optimal Sample Complexity for Single Time-Scale Actor-Critic with Momentum

We establish an optimal sample complexity of $O(ε^{-2})$ for obtaining an $ε$-optimal global policy using a single-timescale actor-critic (AC) algorithm in infinite-horizon discounted Markov decision processes (MDPs) with finite state-action spaces, improving upon the prior state of the art of $O(ε^{-3})$. Our approach applies STORM (STOchastic Recursive Momentum) to reduce variance in the critic updates. However, because samples are drawn from a nonstationary occupancy measure induced by the evolving policy, variance reduction via STORM alone is insufficient. To address this challenge, we maintain a buffer of small fraction of recent samples and uniformly sample from it for each critic update. Importantly, these mechanisms are compatible with existing deep learning architectures and require only minor modifications, without compromising practical applicability.

Policy Gradient with Tree Search: Avoiding Local Optimas through Lookahead

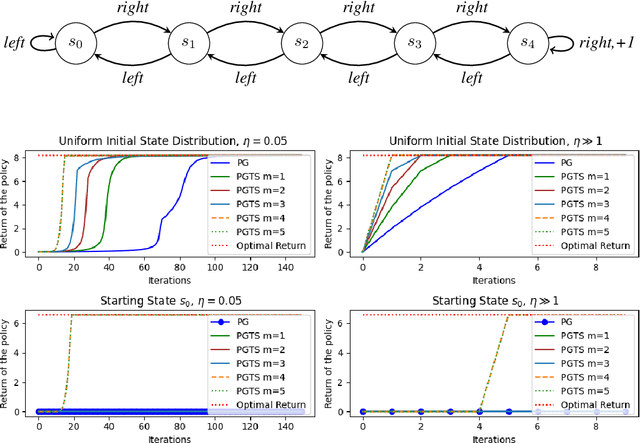
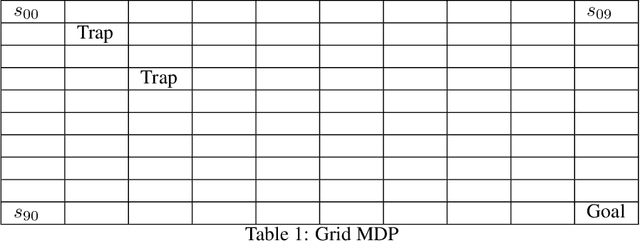
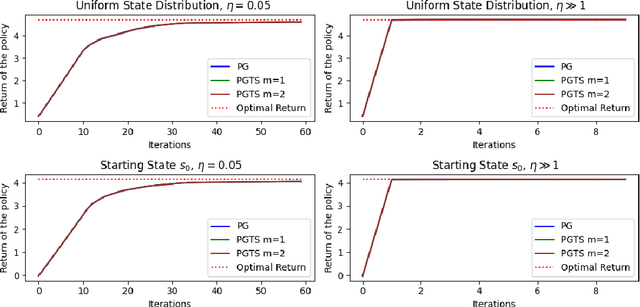
Classical policy gradient (PG) methods in reinforcement learning frequently converge to suboptimal local optima, a challenge exacerbated in large or complex environments. This work investigates Policy Gradient with Tree Search (PGTS), an approach that integrates an $m$-step lookahead mechanism to enhance policy optimization. We provide theoretical analysis demonstrating that increasing the tree search depth $m$-monotonically reduces the set of undesirable stationary points and, consequently, improves the worst-case performance of any resulting stationary policy. Critically, our analysis accommodates practical scenarios where policy updates are restricted to states visited by the current policy, rather than requiring updates across the entire state space. Empirical evaluations on diverse MDP structures, including Ladder, Tightrope, and Gridworld environments, illustrate PGTS's ability to exhibit "farsightedness," navigate challenging reward landscapes, escape local traps where standard PG fails, and achieve superior solutions.

Dual Formulation for Non-Rectangular Lp Robust Markov Decision Processes

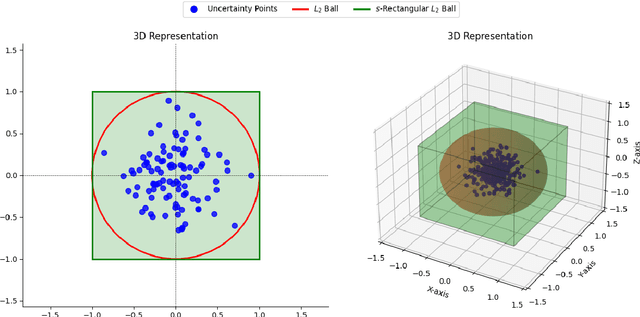
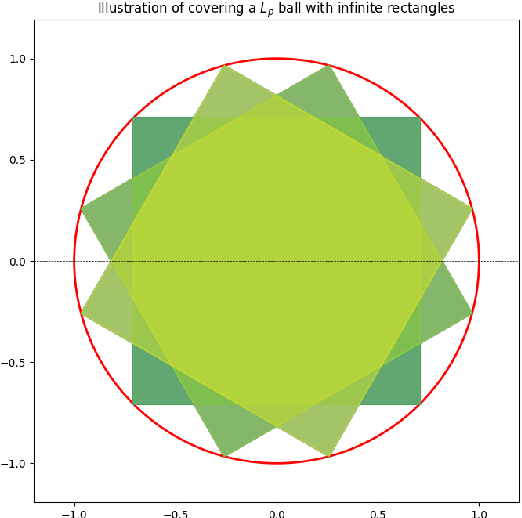
We study robust Markov decision processes (RMDPs) with non-rectangular uncertainty sets, which capture interdependencies across states unlike traditional rectangular models. While non-rectangular robust policy evaluation is generally NP-hard, even in approximation, we identify a powerful class of $L_p$-bounded uncertainty sets that avoid these complexity barriers due to their structural simplicity. We further show that this class can be decomposed into infinitely many \texttt{sa}-rectangular $L_p$-bounded sets and leverage its structural properties to derive a novel dual formulation for $L_p$ RMDPs. This formulation provides key insights into the adversary's strategy and enables the development of the first robust policy evaluation algorithms for non-rectangular RMDPs. Empirical results demonstrate that our approach significantly outperforms brute-force methods, establishing a promising foundation for future investigation into non-rectangular robust MDPs.

Improved Sample Complexity for Global Convergence of Actor-Critic Algorithms

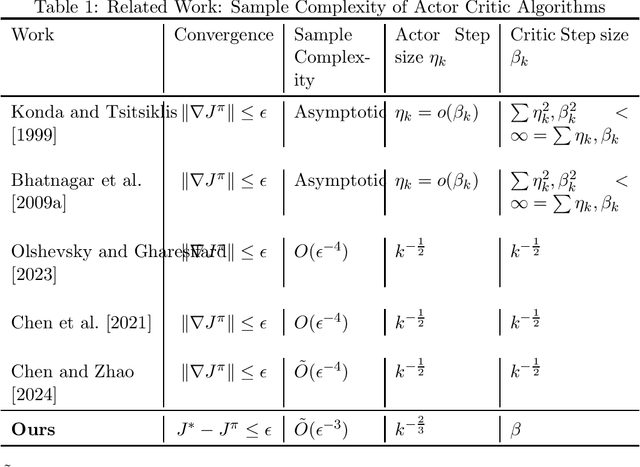
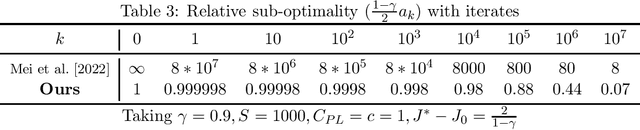
In this paper, we establish the global convergence of the actor-critic algorithm with a significantly improved sample complexity of $O(\epsilon^{-3})$, advancing beyond the existing local convergence results. Previous works provide local convergence guarantees with a sample complexity of $O(\epsilon^{-2})$ for bounding the squared gradient of the return, which translates to a global sample complexity of $O(\epsilon^{-4})$ using the gradient domination lemma. In contrast to traditional methods that employ decreasing step sizes for both the actor and critic, we demonstrate that a constant step size for the critic is sufficient to ensure convergence in expectation. This key insight reveals that using a decreasing step size for the actor alone is sufficient to handle the noise for both the actor and critic. Our findings provide theoretical support for the practical success of many algorithms that rely on constant step sizes.

On the Global Convergence of Policy Gradient in Average Reward Markov Decision Processes

We present the first finite time global convergence analysis of policy gradient in the context of infinite horizon average reward Markov decision processes (MDPs). Specifically, we focus on ergodic tabular MDPs with finite state and action spaces. Our analysis shows that the policy gradient iterates converge to the optimal policy at a sublinear rate of $O\left({\frac{1}{T}}\right),$ which translates to $O\left({\log(T)}\right)$ regret, where $T$ represents the number of iterations. Prior work on performance bounds for discounted reward MDPs cannot be extended to average reward MDPs because the bounds grow proportional to the fifth power of the effective horizon. Thus, our primary contribution is in proving that the policy gradient algorithm converges for average-reward MDPs and in obtaining finite-time performance guarantees. In contrast to the existing discounted reward performance bounds, our performance bounds have an explicit dependence on constants that capture the complexity of the underlying MDP. Motivated by this observation, we reexamine and improve the existing performance bounds for discounted reward MDPs. We also present simulations to empirically evaluate the performance of average reward policy gradient algorithm.

Solving Non-Rectangular Reward-Robust MDPs via Frequency Regularization

In robust Markov decision processes (RMDPs), it is assumed that the reward and the transition dynamics lie in a given uncertainty set. By targeting maximal return under the most adversarial model from that set, RMDPs address performance sensitivity to misspecified environments. Yet, to preserve computational tractability, the uncertainty set is traditionally independently structured for each state. This so-called rectangularity condition is solely motivated by computational concerns. As a result, it lacks a practical incentive and may lead to overly conservative behavior. In this work, we study coupled reward RMDPs where the transition kernel is fixed, but the reward function lies within an $\alpha$-radius from a nominal one. We draw a direct connection between this type of non-rectangular reward-RMDPs and applying policy visitation frequency regularization. We introduce a policy-gradient method, and prove its convergence. Numerical experiments illustrate the learned policy's robustness and its less conservative behavior when compared to rectangular uncertainty.

Robust Reinforcement Learning via Adversarial Kernel Approximation

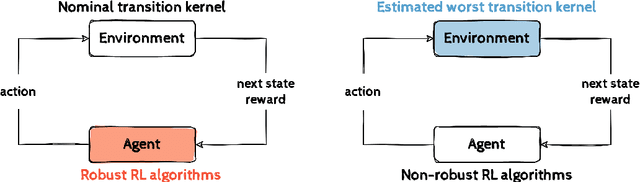
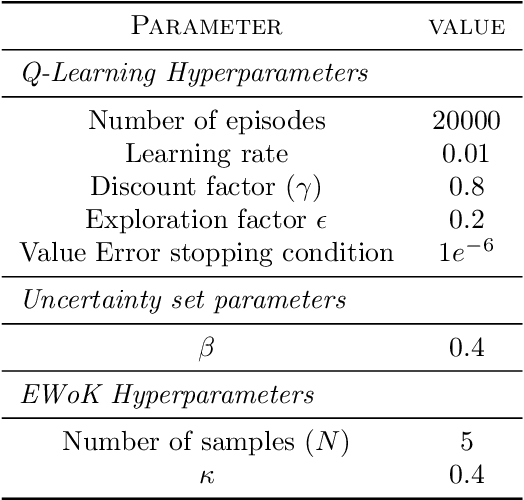
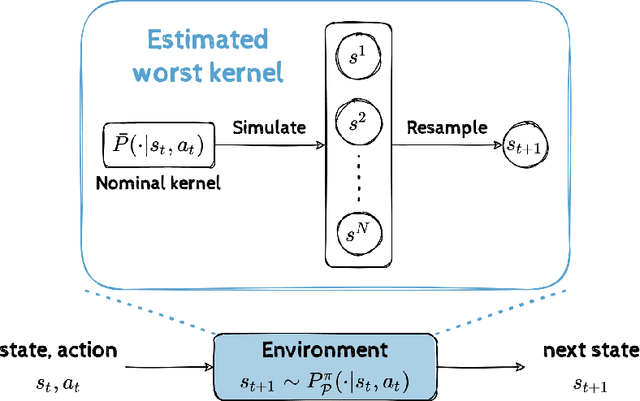
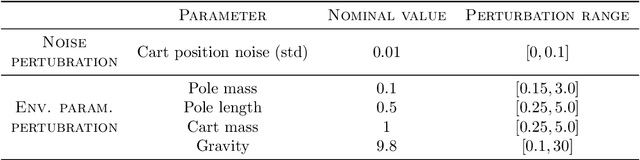
Robust Markov Decision Processes (RMDPs) provide a framework for sequential decision-making that is robust to perturbations on the transition kernel. However, robust reinforcement learning (RL) approaches in RMDPs do not scale well to realistic online settings with high-dimensional domains. By characterizing the adversarial kernel in RMDPs, we propose a novel approach for online robust RL that approximates the adversarial kernel and uses a standard (non-robust) RL algorithm to learn a robust policy. Notably, our approach can be applied on top of any underlying RL algorithm, enabling easy scaling to high-dimensional domains. Experiments in classic control tasks, MinAtar and DeepMind Control Suite demonstrate the effectiveness and the applicability of our method.

Policy Gradient for s-Rectangular Robust Markov Decision Processes

We present a novel robust policy gradient method (RPG) for s-rectangular robust Markov Decision Processes (MDPs). We are the first to derive the adversarial kernel in a closed form and demonstrate that it is a one-rank perturbation of the nominal kernel. This allows us to derive an RPG that is similar to the one used in non-robust MDPs, except with a robust Q-value function and an additional correction term. Both robust Q-values and correction terms are efficiently computable, thus the time complexity of our method matches that of non-robust MDPs, which is significantly faster compared to existing black box methods.

An Efficient Solution to s-Rectangular Robust Markov Decision Processes

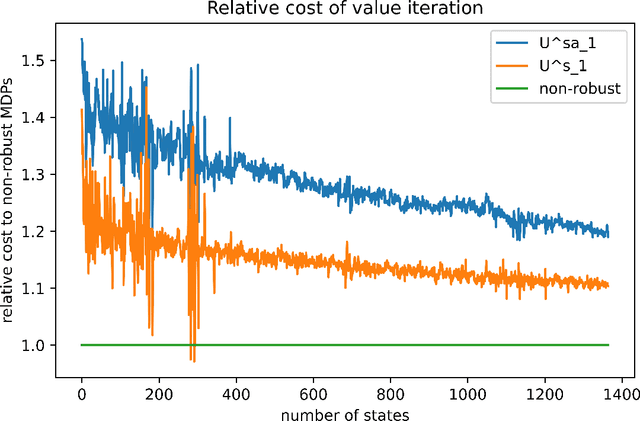
We present an efficient robust value iteration for \texttt{s}-rectangular robust Markov Decision Processes (MDPs) with a time complexity comparable to standard (non-robust) MDPs which is significantly faster than any existing method. We do so by deriving the optimal robust Bellman operator in concrete forms using our $L_p$ water filling lemma. We unveil the exact form of the optimal policies, which turn out to be novel threshold policies with the probability of playing an action proportional to its advantage.

Policy Gradient for Reinforcement Learning with General Utilities

In Reinforcement Learning (RL), the goal of agents is to discover an optimal policy that maximizes the expected cumulative rewards. This objective may also be viewed as finding a policy that optimizes a linear function of its state-action occupancy measure, hereafter referred as Linear RL. However, many supervised and unsupervised RL problems are not covered in the Linear RL framework, such as apprenticeship learning, pure exploration and variational intrinsic control, where the objectives are non-linear functions of the occupancy measures. RL with non-linear utilities looks unwieldy, as methods like Bellman equation, value iteration, policy gradient, dynamic programming that had tremendous success in Linear RL, fail to trivially generalize. In this paper, we derive the policy gradient theorem for RL with general utilities. The policy gradient theorem proves to be a cornerstone in Linear RL due to its elegance and ease of implementability. Our policy gradient theorem for RL with general utilities shares the same elegance and ease of implementability. Based on the policy gradient theorem derived, we also present a simple sample-based algorithm. We believe our results will be of interest to the community and offer inspiration to future works in this generalized setting.