Improved Sample Complexity for Global Convergence of Actor-Critic Algorithms

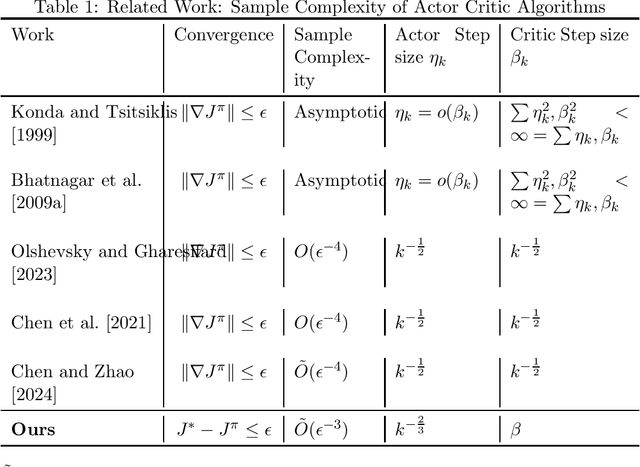
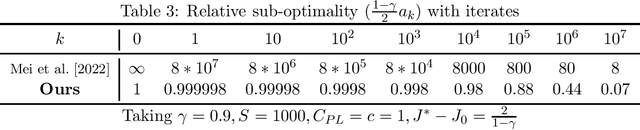
In this paper, we establish the global convergence of the actor-critic algorithm with a significantly improved sample complexity of $O(\epsilon^{-3})$, advancing beyond the existing local convergence results. Previous works provide local convergence guarantees with a sample complexity of $O(\epsilon^{-2})$ for bounding the squared gradient of the return, which translates to a global sample complexity of $O(\epsilon^{-4})$ using the gradient domination lemma. In contrast to traditional methods that employ decreasing step sizes for both the actor and critic, we demonstrate that a constant step size for the critic is sufficient to ensure convergence in expectation. This key insight reveals that using a decreasing step size for the actor alone is sufficient to handle the noise for both the actor and critic. Our findings provide theoretical support for the practical success of many algorithms that rely on constant step sizes.

Optimistic Q-learning for average reward and episodic reinforcement learning

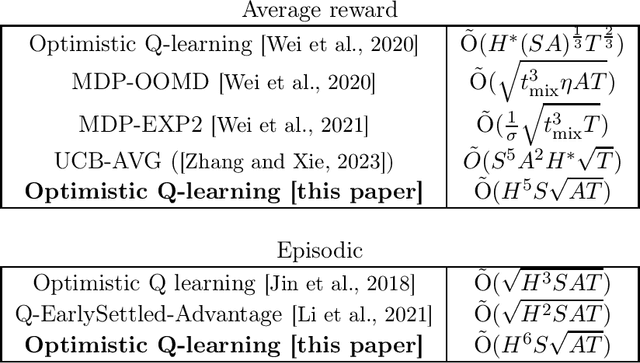
We present an optimistic Q-learning algorithm for regret minimization in average reward reinforcement learning under an additional assumption on the underlying MDP that for all policies, the expected time to visit some frequent state $s_0$ is finite and upper bounded by $H$. Our setting strictly generalizes the episodic setting and is significantly less restrictive than the assumption of bounded hitting time {\it for all states} made by most previous literature on model-free algorithms in average reward settings. We demonstrate a regret bound of $\tilde{O}(H^5 S\sqrt{AT})$, where $S$ and $A$ are the numbers of states and actions, and $T$ is the horizon. A key technical novelty of our work is to introduce an $\overline{L}$ operator defined as $\overline{L} v = \frac{1}{H} \sum_{h=1}^H L^h v$ where $L$ denotes the Bellman operator. We show that under the given assumption, the $\overline{L}$ operator has a strict contraction (in span) even in the average reward setting. Our algorithm design then uses ideas from episodic Q-learning to estimate and apply this operator iteratively. Therefore, we provide a unified view of regret minimization in episodic and non-episodic settings that may be of independent interest.

Improved Optimistic Algorithm For The Multinomial Logit Contextual Bandit

We consider a dynamic assortment selection problem where the goal is to offer a sequence of assortments of cardinality at most $K$, out of $N$ items, to minimize the expected cumulative regret (loss of revenue). The feedback is given by a multinomial logit (MNL) choice model. This sequential decision making problem is studied under the MNL contextual bandit framework. The existing algorithms for MNL contexual bandit have frequentist regret guarantees as $\tilde{\mathrm{O}}(\kappa\sqrt{T})$, where $\kappa$ is an instance dependent constant. $\kappa$ could be arbitrarily large, e.g. exponentially dependent on the model parameters, causing the existing regret guarantees to be substantially loose. We propose an optimistic algorithm with a carefully designed exploration bonus term and show that it enjoys $\tilde{\mathrm{O}}(\sqrt{T})$ regret. In our bounds, the $\kappa$ factor only affects the poly-log term and not the leading term of the regret bounds.

Improved Worst-Case Regret Bounds for Randomized Least-Squares Value Iteration

This paper studies regret minimization with randomized value functions in reinforcement learning. In tabular finite-horizon Markov Decision Processes, we introduce a clipping variant of one classical Thompson Sampling (TS)-like algorithm, randomized least-squares value iteration (RLSVI). We analyze the algorithm using a novel intertwined regret decomposition. Our $\tilde{\mathrm{O}}(H^2S\sqrt{AT})$ high-probability worst-case regret bound improves the previous sharpest worst-case regret bounds for RLSVI and matches the existing state-of-the-art worst-case TS-based regret bounds.

Learning by Repetition: Stochastic Multi-armed Bandits under Priming Effect

We study the effect of persistence of engagement on learning in a stochastic multi-armed bandit setting. In advertising and recommendation systems, repetition effect includes a wear-in period, where the user's propensity to reward the platform via a click or purchase depends on how frequently they see the recommendation in the recent past. It also includes a counteracting wear-out period, where the user's propensity to respond positively is dampened if the recommendation was shown too many times recently. Priming effect can be naturally modelled as a temporal constraint on the strategy space, since the reward for the current action depends on historical actions taken by the platform. We provide novel algorithms that achieves sublinear regret in time and the relevant wear-in/wear-out parameters. The effect of priming on the regret upper bound is also additive, and we get back a guarantee that matches popular algorithms such as the UCB1 and Thompson sampling when there is no priming effect. Our work complements recent work on modeling time varying rewards, delays and corruptions in bandits, and extends the usage of rich behavior models in sequential decision making settings.

Incentivising Exploration and Recommendations for Contextual Bandits with Payments

We propose a contextual bandit based model to capture the learning and social welfare goals of a web platform in the presence of myopic users. By using payments to incentivize these agents to explore different items/recommendations, we show how the platform can learn the inherent attributes of items and achieve a sublinear regret while maximizing cumulative social welfare. We also calculate theoretical bounds on the cumulative costs of incentivization to the platform. Unlike previous works in this domain, we consider contexts to be completely adversarial, and the behavior of the adversary is unknown to the platform. Our approach can improve various engagement metrics of users on e-commerce stores, recommendation engines and matching platforms.

Bandits with Temporal Stochastic Constraints

We study the effect of impairment on stochastic multi-armed bandits and develop new ways to mitigate it. Impairment effect is the phenomena where an agent only accrues reward for an action if they have played it at least a few times in the recent past. It is practically motivated by repetition and recency effects in domains such as advertising (here consumer behavior may require repeat actions by advertisers) and vocational training (here actions are complex skills that can only be mastered with repetition to get a payoff). Impairment can be naturally modelled as a temporal constraint on the strategy space, and we provide two novel algorithms that achieve sublinear regret, each working with different assumptions on the impairment effect. We introduce a new notion called bucketing in our algorithm design, and show how it can effectively address impairment as well as a broader class of temporal constraints. Our regret bounds explicitly capture the cost of impairment and show that it scales (sub-)linearly with the degree of impairment. Our work complements recent work on modeling delays and corruptions, and we provide experimental evidence supporting our claims.