Optimistic Q-learning for average reward and episodic reinforcement learning

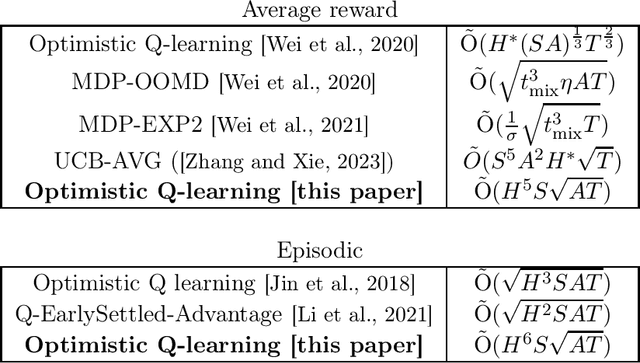
We present an optimistic Q-learning algorithm for regret minimization in average reward reinforcement learning under an additional assumption on the underlying MDP that for all policies, the expected time to visit some frequent state $s_0$ is finite and upper bounded by $H$. Our setting strictly generalizes the episodic setting and is significantly less restrictive than the assumption of bounded hitting time {\it for all states} made by most previous literature on model-free algorithms in average reward settings. We demonstrate a regret bound of $\tilde{O}(H^5 S\sqrt{AT})$, where $S$ and $A$ are the numbers of states and actions, and $T$ is the horizon. A key technical novelty of our work is to introduce an $\overline{L}$ operator defined as $\overline{L} v = \frac{1}{H} \sum_{h=1}^H L^h v$ where $L$ denotes the Bellman operator. We show that under the given assumption, the $\overline{L}$ operator has a strict contraction (in span) even in the average reward setting. Our algorithm design then uses ideas from episodic Q-learning to estimate and apply this operator iteratively. Therefore, we provide a unified view of regret minimization in episodic and non-episodic settings that may be of independent interest.

Dynamic Pricing and Learning with Long-term Reference Effects

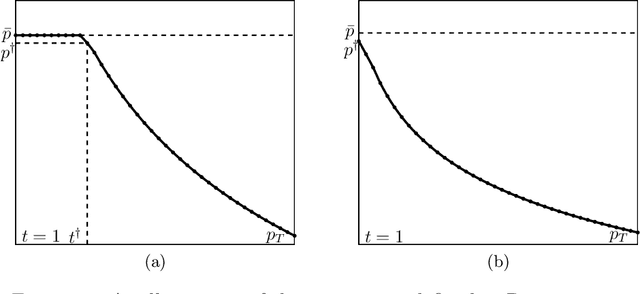
We consider a dynamic pricing problem where customer response to the current price is impacted by the customer price expectation, aka reference price. We study a simple and novel reference price mechanism where reference price is the average of the past prices offered by the seller. As opposed to the more commonly studied exponential smoothing mechanism, in our reference price mechanism the prices offered by seller have a longer term effect on the future customer expectations. We show that under this mechanism, a markdown policy is near-optimal irrespective of the parameters of the model. This matches the common intuition that a seller may be better off by starting with a higher price and then decreasing it, as the customers feel like they are getting bargains on items that are ordinarily more expensive. For linear demand models, we also provide a detailed characterization of the near-optimal markdown policy along with an efficient way of computing it. We then consider a more challenging dynamic pricing and learning problem, where the demand model parameters are apriori unknown, and the seller needs to learn them online from the customers' responses to the offered prices while simultaneously optimizing revenue. The objective is to minimize regret, i.e., the $T$-round revenue loss compared to a clairvoyant optimal policy. This task essentially amounts to learning a non-stationary optimal policy in a time-variant Markov Decision Process (MDP). For linear demand models, we provide an efficient learning algorithm with an optimal $\tilde{O}(\sqrt{T})$ regret upper bound.

Dynamic Pricing and Learning with Bayesian Persuasion

We consider a novel dynamic pricing and learning setting where in addition to setting prices of products in sequential rounds, the seller also ex-ante commits to 'advertising schemes'. That is, in the beginning of each round the seller can decide what kind of signal they will provide to the buyer about the product's quality upon realization. Using the popular Bayesian persuasion framework to model the effect of these signals on the buyers' valuation and purchase responses, we formulate the problem of finding an optimal design of the advertising scheme along with a pricing scheme that maximizes the seller's expected revenue. Without any apriori knowledge of the buyers' demand function, our goal is to design an online algorithm that can use past purchase responses to adaptively learn the optimal pricing and advertising strategy. We study the regret of the algorithm when compared to the optimal clairvoyant price and advertising scheme. Our main result is a computationally efficient online algorithm that achieves an $O(T^{2/3}(m\log T)^{1/3})$ regret bound when the valuation function is linear in the product quality. Here $m$ is the cardinality of the discrete product quality domain and $T$ is the time horizon. This result requires some natural monotonicity and Lipschitz assumptions on the valuation function, but no Lipschitz or smoothness assumption on the buyers' demand function. For constant $m$, our result matches the regret lower bound for dynamic pricing within logarithmic factors, which is a special case of our problem. We also obtain several improved results for the widely considered special case of additive valuations, including an $\tilde{O}(T^{2/3})$ regret bound independent of $m$ when $m\le T^{1/3}$.

Online Allocation and Learning in the Presence of Strategic Agents

We study the problem of allocating $T$ sequentially arriving items among $n$ homogeneous agents under the constraint that each agent must receive a pre-specified fraction of all items, with the objective of maximizing the agents' total valuation of items allocated to them. The agents' valuations for the item in each round are assumed to be i.i.d. but their distribution is a priori unknown to the central planner. Therefore, the central planner needs to implicitly learn these distributions from the observed values in order to pick a good allocation policy. However, an added challenge here is that the agents are strategic with incentives to misreport their valuations in order to receive better allocations. This sets our work apart both from the online auction design settings which typically assume known valuation distributions and/or involve payments, and from the online learning settings that do not consider strategic agents. To that end, our main contribution is an online learning based allocation mechanism that is approximately Bayesian incentive compatible, and when all agents are truthful, guarantees a sublinear regret for individual agents' utility compared to that under the optimal offline allocation policy.

Scale Free Adversarial Multi Armed Bandits

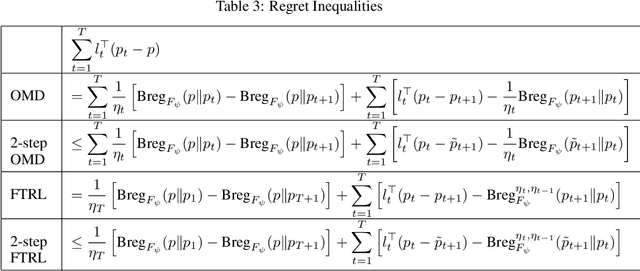
We consider the Scale-Free Adversarial Multi Armed Bandit(MAB) problem, where the player only knows the number of arms $n$ and not the scale or magnitude of the losses. It sees bandit feedback about the loss vectors $l_1,\dots, l_T \in \mathbb{R}^n$. The goal is to bound its regret as a function of $n$ and $l_1,\dots, l_T$. We design a Follow The Regularized Leader(FTRL) algorithm, which comes with the first scale-free regret guarantee for MAB. It uses the log barrier regularizer, the importance weighted estimator, an adaptive learning rate, and an adaptive exploration parameter. In the analysis, we introduce a simple, unifying technique for obtaining regret inequalities for FTRL and Online Mirror Descent(OMD) on the probability simplex using Potential Functions and Mixed Bregmans. We also develop a new technique for obtaining local-norm lower bounds for Bregman Divergences, which are crucial in bandit regret bounds. These tools could be of independent interest.

Dynamic Pricing and Learning under the Bass Model

We consider a novel formulation of the dynamic pricing and demand learning problem, where the evolution of demand in response to posted prices is governed by a stochastic variant of the popular Bass model with parameters $\alpha, \beta$ that are linked to the so-called "innovation" and "imitation" effects. Unlike the more commonly used i.i.d. and contextual demand models, in this model the posted price not only affects the demand and the revenue in the current round but also the future evolution of demand, and hence the fraction of potential market size $m$ that can be ultimately captured. In this paper, we consider the more challenging incomplete information problem where dynamic pricing is applied in conjunction with learning the unknown parameters, with the objective of optimizing the cumulative revenues over a given selling horizon of length $T$. Equivalently, the goal is to minimize the regret which measures the revenue loss of the algorithm relative to the optimal expected revenue achievable under the stochastic Bass model with market size $m$ and time horizon $T$. Our main contribution is the development of an algorithm that satisfies a high probability regret guarantee of order $\tilde O(m^{2/3})$; where the market size $m$ is known a priori. Moreover, we show that no algorithm can incur smaller order of loss by deriving a matching lower bound. Unlike most regret analysis results, in the present problem the market size $m$ is the fundamental driver of the complexity; our lower bound in fact, indicates that for any fixed $\alpha, \beta$, most non-trivial instances of the problem have constant $T$ and large $m$. We believe that this insight sets the problem of dynamic pricing under the Bass model apart from the typical i.i.d. setting and multi-armed bandit based models for dynamic pricing, which typically focus only on the asymptotics with respect to time horizon $T$.

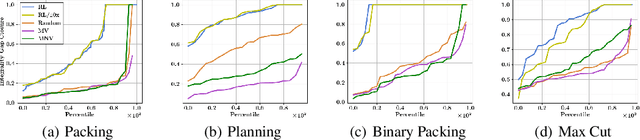
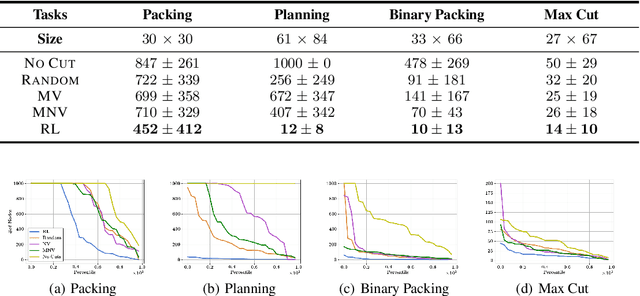
Reinforcement Learning for Integer Programming: Learning to Cut

Integer programming (IP) is a general optimization framework widely applicable to a variety of unstructured and structured problems arising in, e.g., scheduling, production planning, and graph optimization. As IP models many provably hard to solve problems, modern IP solvers rely on many heuristics. These heuristics are usually human-designed, and naturally prone to suboptimality. The goal of this work is to show that the performance of those solvers can be greatly enhanced using reinforcement learning (RL). In particular, we investigate a specific methodology for solving IPs, known as the Cutting Plane Method. This method is employed as a subroutine by all modern IP solvers. We present a deep RL formulation, network architecture, and algorithms for intelligent adaptive selection of cutting planes (aka cuts). Across a wide range of IP tasks, we show that the trained RL agent significantly outperforms human-designed heuristics, and effectively generalizes to 10X larger instances and across IP problem classes. The trained agent is also demonstrated to benefit the popular downstream application of cutting plane methods in Branch-and-Cut algorithm, which is the backbone of state-of-the-art commercial IP solvers.

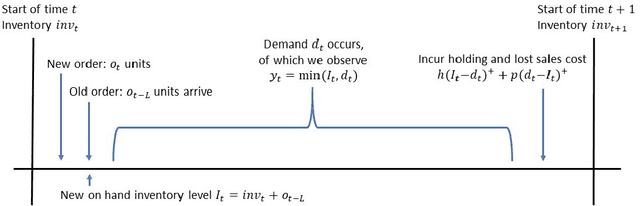
Learning in structured MDPs with convex cost functions: Improved regret bounds for inventory management

We consider a stochastic inventory control problem under censored demands, lost sales, and positive lead times. This is a fundamental problem in inventory management, with significant literature establishing near-optimality of a simple class of policies called ``base-stock policies'' for the underlying Markov Decision Process (MDP), as well as convexity of long run average-cost under those policies. We consider the relatively less studied problem of designing a learning algorithm for this problem when the underlying demand distribution is unknown. The goal is to bound regret of the algorithm when compared to the best base-stock policy. We utilize the convexity properties and a newly derived bound on bias of base-stock policies to establish a connection to stochastic convex bandit optimization. Our main contribution is a learning algorithm with a regret bound of $\tilde{O}(L\sqrt{T}+D)$ for the inventory control problem. Here $L$ is the fixed and known lead time, and $D$ is an unknown parameter of the demand distribution described roughly as the number of time steps needed to generate enough demand for depleting one unit of inventory. Notably, even though the state space of the underlying MDP is continuous and $L$-dimensional, our regret bounds depend linearly on $L$. Our results significantly improve the previously best known regret bounds for this problem where the dependence on $L$ was exponential and many further assumptions on demand distribution were required. The techniques presented here may be of independent interest for other settings that involve large structured MDPs but with convex cost functions.

Discretizing Continuous Action Space for On-Policy Optimization

In this work, we show that discretizing action space for continuous control is a simple yet powerful technique for on-policy optimization. The explosion in the number of discrete actions can be efficiently addressed by a policy with factorized distribution across action dimensions. We show that the discrete policy achieves significant performance gains with state-of-the-art on-policy optimization algorithms (PPO, TRPO, ACKTR) especially on high-dimensional tasks with complex dynamics. Additionally, we show that an ordinal parameterization of the discrete distribution can introduce the inductive bias that encodes the natural ordering between discrete actions. This ordinal architecture further significantly improves the performance of PPO/TRPO.

Thompson Sampling for the MNL-Bandit

We consider a sequential subset selection problem under parameter uncertainty, where at each time step, the decision maker selects a subset of cardinality $K$ from $N$ possible items (arms), and observes a (bandit) feedback in the form of the index of one of the items in said subset, or none. Each item in the index set is ascribed a certain value (reward), and the feedback is governed by a Multinomial Logit (MNL) choice model whose parameters are a priori unknown. The objective of the decision maker is to maximize the expected cumulative rewards over a finite horizon $T$, or alternatively, minimize the regret relative to an oracle that knows the MNL parameters. We refer to this as the MNL-Bandit problem. This problem is representative of a larger family of exploration-exploitation problems that involve a combinatorial objective, and arise in several important application domains. We present an approach to adapt Thompson Sampling to this problem and show that it achieves near-optimal regret as well as attractive numerical performance.