Fully Dynamic Online Selection through Online Contention Resolution Schemes

We study fully dynamic online selection problems in an adversarial/stochastic setting that includes Bayesian online selection, prophet inequalities, posted price mechanisms, and stochastic probing problems subject to combinatorial constraints. In the classical ``incremental'' version of the problem, selected elements remain active until the end of the input sequence. On the other hand, in the fully dynamic version of the problem, elements stay active for a limited time interval, and then leave. This models, for example, the online matching of tasks to workers with task/worker-dependent working times, and sequential posted pricing of perishable goods. A successful approach to online selection problems in the adversarial setting is given by the notion of Online Contention Resolution Scheme (OCRS), that uses a priori information to formulate a linear relaxation of the underlying optimization problem, whose optimal fractional solution is rounded online for any adversarial order of the input sequence. Our main contribution is providing a general method for constructing an OCRS for fully dynamic online selection problems. Then, we show how to employ such OCRS to construct no-regret algorithms in a partial information model with semi-bandit feedback and adversarial inputs.

Bandits for Online Calibration: An Application to Content Moderation on Social Media Platforms

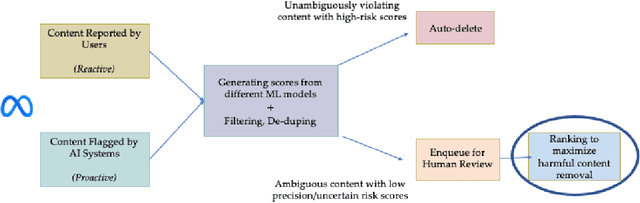
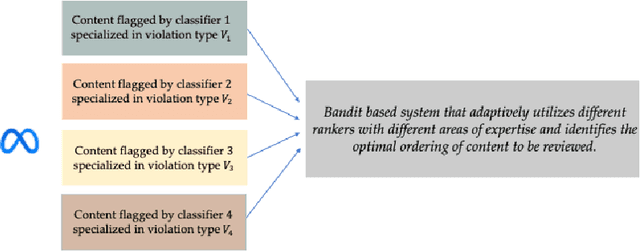
We describe the current content moderation strategy employed by Meta to remove policy-violating content from its platforms. Meta relies on both handcrafted and learned risk models to flag potentially violating content for human review. Our approach aggregates these risk models into a single ranking score, calibrating them to prioritize more reliable risk models. A key challenge is that violation trends change over time, affecting which risk models are most reliable. Our system additionally handles production challenges such as changing risk models and novel risk models. We use a contextual bandit to update the calibration in response to such trends. Our approach increases Meta's top-line metric for measuring the effectiveness of its content moderation strategy by 13%.

Top $K$ Ranking for Multi-Armed Bandit with Noisy Evaluations

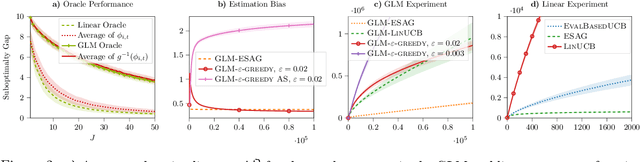
We consider a multi-armed bandit setting where, at the beginning of each round, the learner receives noisy independent, and possibly biased, \emph{evaluations} of the true reward of each arm and it selects $K$ arms with the objective of accumulating as much reward as possible over $T$ rounds. Under the assumption that at each round the true reward of each arm is drawn from a fixed distribution, we derive different algorithmic approaches and theoretical guarantees depending on how the evaluations are generated. First, we show a $\widetilde{O}(T^{2/3})$ regret in the general case when the observation functions are a genearalized linear function of the true rewards. On the other hand, we show that an improved $\widetilde{O}(\sqrt{T})$ regret can be derived when the observation functions are noisy linear functions of the true rewards. Finally, we report an empirical validation that confirms our theoretical findings, provides a thorough comparison to alternative approaches, and further supports the interest of this setting in practice.

QUEST: Queue Simulation for Content Moderation at Scale

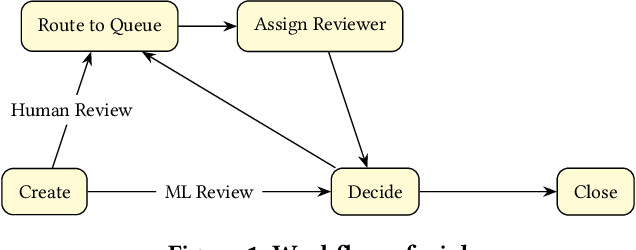
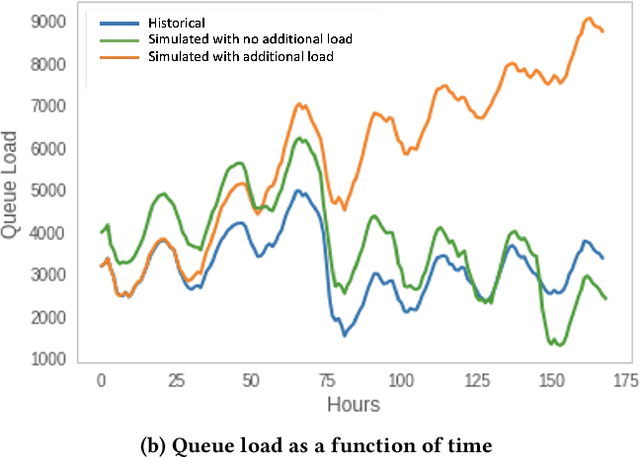
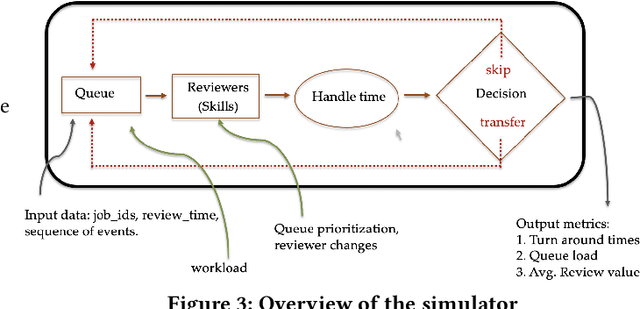
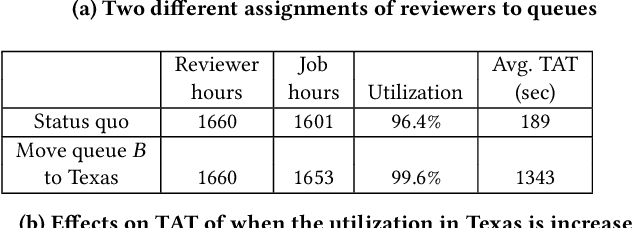
Moderating content in social media platforms is a formidable challenge due to the unprecedented scale of such systems, which typically handle billions of posts per day. Some of the largest platforms such as Facebook blend machine learning with manual review of platform content by thousands of reviewers. Operating a large-scale human review system poses interesting and challenging methodological questions that can be addressed with operations research techniques. We investigate the problem of optimally operating such a review system at scale using ideas from queueing theory and simulation.

Stochastic Bandits for Multi-platform Budget Optimization in Online Advertising

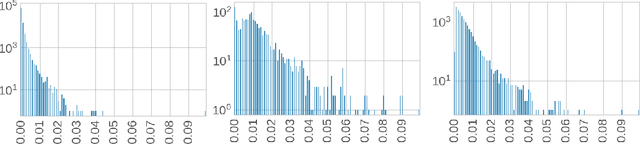
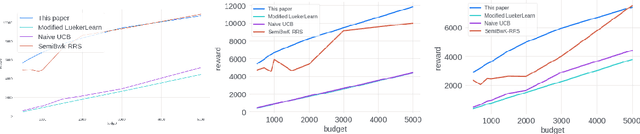
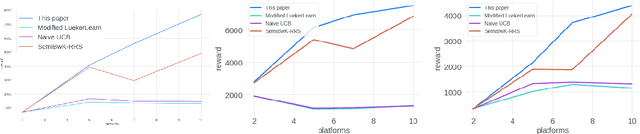
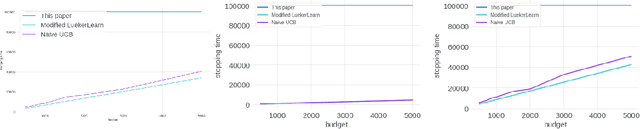
We study the problem of an online advertising system that wants to optimally spend an advertiser's given budget for a campaign across multiple platforms, without knowing the value for showing an ad to the users on those platforms. We model this challenging practical application as a Stochastic Bandits with Knapsacks problem over $T$ rounds of bidding with the set of arms given by the set of distinct bidding $m$-tuples, where $m$ is the number of platforms. We modify the algorithm proposed in Badanidiyuru \emph{et al.,} to extend it to the case of multiple platforms to obtain an algorithm for both the discrete and continuous bid-spaces. Namely, for discrete bid spaces we give an algorithm with regret $O\left(OPT \sqrt {\frac{mn}{B} }+ \sqrt{mn OPT}\right)$, where $OPT$ is the performance of the optimal algorithm that knows the distributions. For continuous bid spaces the regret of our algorithm is $\tilde{O}\left(m^{1/3} \cdot \min\left\{ B^{2/3}, (m T)^{2/3} \right\} \right)$. When restricted to this special-case, this bound improves over Sankararaman and Slivkins in the regime $OPT \ll T$, as is the case in the particular application at hand. Second, we show an $ \Omega\left (\sqrt {m OPT} \right)$ lower bound for the discrete case and an $\Omega\left( m^{1/3} B^{2/3}\right)$ lower bound for the continuous setting, almost matching the upper bounds. Finally, we use a real-world data set from a large internet online advertising company with multiple ad platforms and show that our algorithms outperform common benchmarks and satisfy the required properties warranted in the real-world application.

Improved Optimistic Algorithm For The Multinomial Logit Contextual Bandit

We consider a dynamic assortment selection problem where the goal is to offer a sequence of assortments of cardinality at most $K$, out of $N$ items, to minimize the expected cumulative regret (loss of revenue). The feedback is given by a multinomial logit (MNL) choice model. This sequential decision making problem is studied under the MNL contextual bandit framework. The existing algorithms for MNL contexual bandit have frequentist regret guarantees as $\tilde{\mathrm{O}}(\kappa\sqrt{T})$, where $\kappa$ is an instance dependent constant. $\kappa$ could be arbitrarily large, e.g. exponentially dependent on the model parameters, causing the existing regret guarantees to be substantially loose. We propose an optimistic algorithm with a carefully designed exploration bonus term and show that it enjoys $\tilde{\mathrm{O}}(\sqrt{T})$ regret. In our bounds, the $\kappa$ factor only affects the poly-log term and not the leading term of the regret bounds.

Multi-armed Bandits with Cost Subsidy

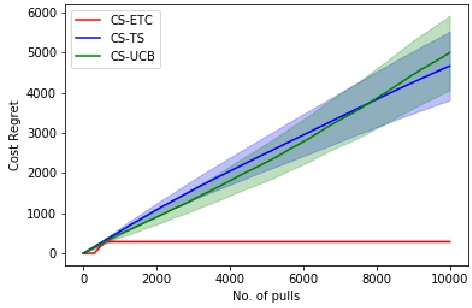
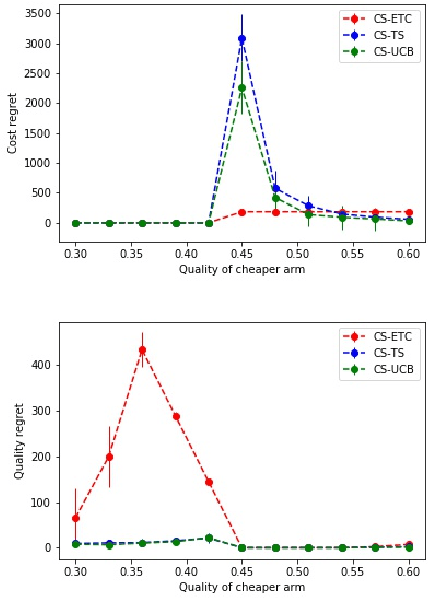
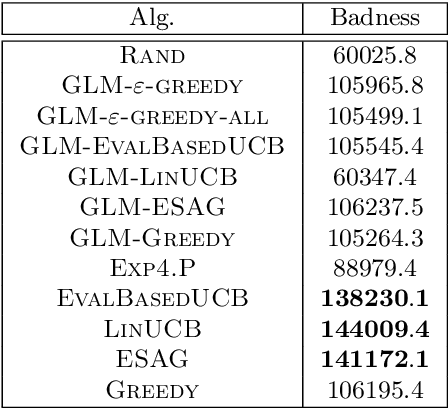
In this paper, we consider a novel variant of the multi-armed bandit (MAB) problem, MAB with cost subsidy, which models many real-life applications where the learning agent has to pay to select an arm and is concerned about optimizing cumulative costs and rewards. We present two applications, intelligent SMS routing problem and ad audience optimization problem faced by a number of businesses (especially online platforms) and show how our problem uniquely captures key features of these applications. We show that naive generalizations of existing MAB algorithms like Upper Confidence Bound and Thompson Sampling do not perform well for this problem. We then establish fundamental lower bound of $\Omega(K^{1/3} T^{2/3})$ on the performance of any online learning algorithm for this problem, highlighting the hardness of our problem in comparison to the classical MAB problem (where $T$ is the time horizon and $K$ is the number of arms). We also present a simple variant of explore-then-commit and establish near-optimal regret bounds for this algorithm. Lastly, we perform extensive numerical simulations to understand the behavior of a suite of algorithms for various instances and recommend a practical guide to employ different algorithms.

Thompson Sampling for Contextual Bandit Problems with Auxiliary Safety Constraints

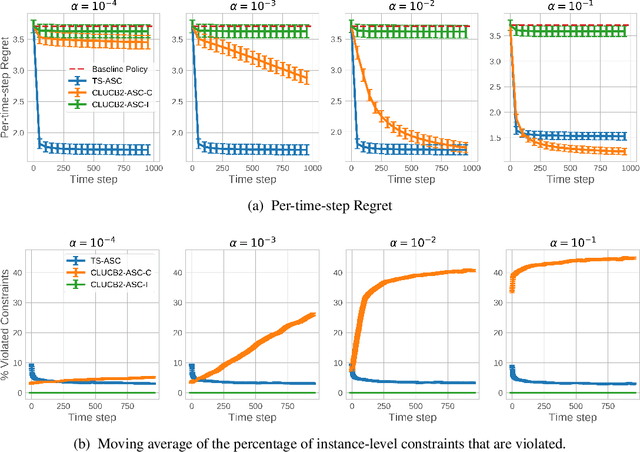
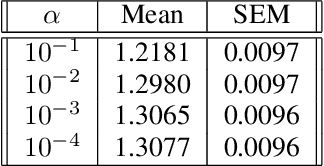
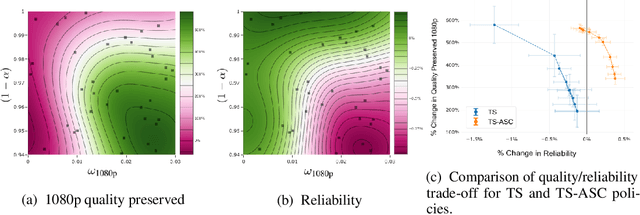
Recent advances in contextual bandit optimization and reinforcement learning have garnered interest in applying these methods to real-world sequential decision making problems. Real-world applications frequently have constraints with respect to a currently deployed policy. Many of the existing constraint-aware algorithms consider problems with a single objective (the reward) and a constraint on the reward with respect to a baseline policy. However, many important applications involve multiple competing objectives and auxiliary constraints. In this paper, we propose a novel Thompson sampling algorithm for multi-outcome contextual bandit problems with auxiliary constraints. We empirically evaluate our algorithm on a synthetic problem. Lastly, we apply our method to a real world video transcoding problem and provide a practical way for navigating the trade-off between safety and performance using Bayesian optimization.

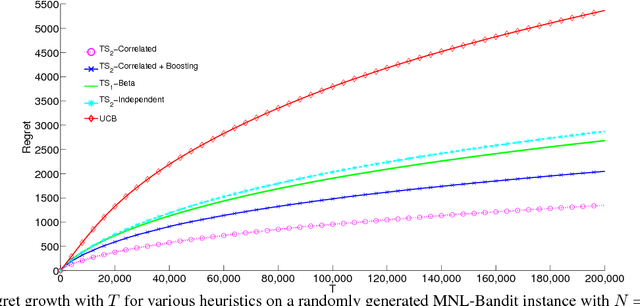
Thompson Sampling for the MNL-Bandit

We consider a sequential subset selection problem under parameter uncertainty, where at each time step, the decision maker selects a subset of cardinality $K$ from $N$ possible items (arms), and observes a (bandit) feedback in the form of the index of one of the items in said subset, or none. Each item in the index set is ascribed a certain value (reward), and the feedback is governed by a Multinomial Logit (MNL) choice model whose parameters are a priori unknown. The objective of the decision maker is to maximize the expected cumulative rewards over a finite horizon $T$, or alternatively, minimize the regret relative to an oracle that knows the MNL parameters. We refer to this as the MNL-Bandit problem. This problem is representative of a larger family of exploration-exploitation problems that involve a combinatorial objective, and arise in several important application domains. We present an approach to adapt Thompson Sampling to this problem and show that it achieves near-optimal regret as well as attractive numerical performance.

MNL-Bandit: A Dynamic Learning Approach to Assortment Selection

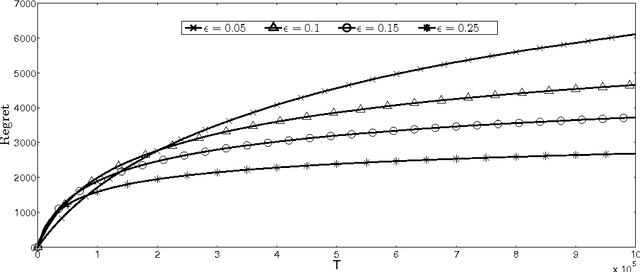
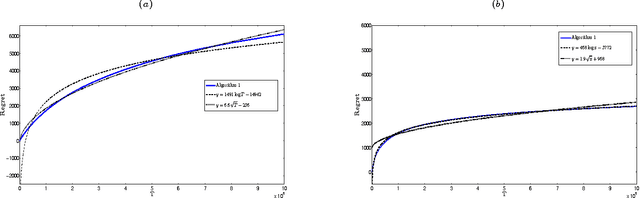
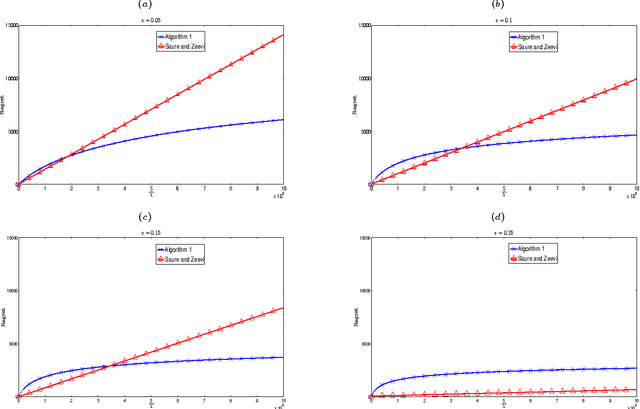
We consider a dynamic assortment selection problem, where in every round the retailer offers a subset (assortment) of $N$ substitutable products to a consumer, who selects one of these products according to a multinomial logit (MNL) choice model. The retailer observes this choice and the objective is to dynamically learn the model parameters, while optimizing cumulative revenues over a selling horizon of length $T$. We refer to this exploration-exploitation formulation as the MNL-Bandit problem. Existing methods for this problem follow an "explore-then-exploit" approach, which estimate parameters to a desired accuracy and then, treating these estimates as if they are the correct parameter values, offers the optimal assortment based on these estimates. These approaches require certain a priori knowledge of "separability", determined by the true parameters of the underlying MNL model, and this in turn is critical in determining the length of the exploration period. (Separability refers to the distinguishability of the true optimal assortment from the other sub-optimal alternatives.) In this paper, we give an efficient algorithm that simultaneously explores and exploits, achieving performance independent of the underlying parameters. The algorithm can be implemented in a fully online manner, without knowledge of the horizon length $T$. Furthermore, the algorithm is adaptive in the sense that its performance is near-optimal in both the "well separated" case, as well as the general parameter setting where this separation need not hold.