Terminal Dimension Reduction for Time Series with Applications

Terminal embeddings have emerged as a powerful tool for dimension reduction. Given a set of points $P\subset \mathbb{R}^d$, a terminal embedding is a mapping $f:\mathbb{R}^d\rightarrow \mathbb{R}^t$ that preserves the pairwise distance between any pair of points $p\in P$ and $q\in \mathbb{R}^d$ up to small distortion under this mapping. Terminal embeddings have been particularly fruitful for constructing $k$-means and $k$-median coresets, where the objective is to find a typically weighted subset $Ω$ of $P$ such that for any candidate solution, the cost of the clustering objective on $Ω$ approximates the cost of the clustering objective on $P$ up to small distortion. Unfortunately, these techniques have not been extended to more complicated structures such as clustering time-series data under common straight-line interpolation between measurements. The main issue is that terminal embeddings, arguably the central technique in this line of research, cannot be linear and are thus not immediately suitable to preserve linear structures. In this work, we develop a generalization of terminal embeddings to affine line-segments that overcomes this issue. We showcase their applicability by using our lines-preserving terminal embeddings to obtain the first dimension-free coresets for clustering time-series under the Fréchet distance. The underlying dimension reduction uses Johnson-Lindenstrauss (JL) embeddings, and our experiments indicate that terminal embeddings perform similarly to JL and favorably against PCA for synthetic and real-world time-series, while only terminal embeddings extend pairwise distance preservation to the full ambient space.

Online Convex Optimization with Sublinear Noisy Probes

We study Online Convex Optimization (OCO) over a convex set $K\subseteq \mathbb R^d$, where in each round $t$ the learner selects $x_t\in K$ and then observes a convex loss $f_t:K\to[0,1]$, with the goal of minimizing regret to the best fixed decision in hindsight. We introduce a unified probing model that generalizes two recent lines of work: sublinear best-expert queries in the experts setting, and pairwise (comparison-based) feedback available every round in OCO. In our framework, the learner has a budget of $k\le T$ pairwise probes; on a probed round it may query two points and learn which one has smaller loss. Our main result shows that even a sublinear and noisy probe budget can provably improve worst-case regret in the full feedback OCO regime. With $k$ $δ$-noisy pairwise probes, we obtain: $ \text{Reg}_T \le O\left(\min\left\{\sqrt{dT\ln T},\; \frac{dT\ln T}{k|1-2δ|}\right\}\right) $, which is tight (up to logarithmic factors in $T$) across $T$, $k$ and $δ$. Specifically regarding the noise parameter $δ\in [0,1]$, the regret guarantee smoothly degrades as the oracle response approaches a coin flip, i.e., $δ$ is close to $\frac{1}{2}$. When applying the same techniques to a finite $K$ for the prediction with $d$ experts setting, the resulting rates are instead completely tight in all parameters, including $d$. Our analysis gives a streamlined treatment of pairwise probing in OCO by quantifying the benefit of probing via a variance reduction effect, combined with a second-order (variance-based) analysis of Continuous Exponential Weights.

Contextual Online Bilateral Trade

We study repeated bilateral trade when the valuations of the sellers and the buyers are contextual. More precisely, the agents' valuations are given by the inner product of a context vector with two unknown $d$-dimensional vectors -- one for the buyers and one for the sellers. At each time step $t$, the learner receives a context and posts two prices, one for the seller and one for the buyer, and the trade happens if both agents accept their price. We study two objectives for this problem, gain from trade and profit, proving no-regret with respect to a surprisingly strong benchmark: the best omniscient dynamic strategy. In the natural scenario where the learner observes \emph{separately} whether the agents accept their price -- the so-called \emph{two-bit} feedback -- we design algorithms that achieve $O(d\log d)$ regret for gain from trade, and $O(d \log\log T + d\log d)$ regret for profit maximization. Both results are tight, up to the $\log(d)$ factor, and implement per-step budget balance, meaning that the learner never incurs negative profit. In the less informative \emph{one-bit} feedback model, the learner only observes whether a trade happens or not. For this scenario, we show that the tight two-bit regret regimes are still attainable, at the cost of allowing the learner to possibly incur a small negative profit of order $O(d\log d)$, which is notably independent of the time horizon. As a final set of results, we investigate the combination of one-bit feedback and per-step budget balance. There, we design an algorithm for gain from trade that suffers regret independent of the time horizon, but \emph{exponential} in the dimension $d$. For profit maximization, we maintain this exponential dependence on the dimension, which gets multiplied by a $\log T$ factor.

Multicalibration yields better matchings

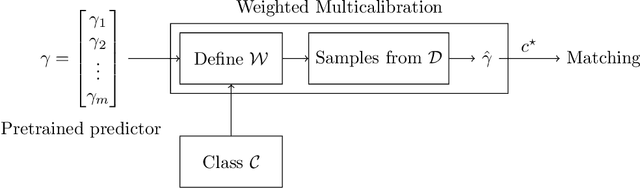
Consider the problem of finding the best matching in a weighted graph where we only have access to predictions of the actual stochastic weights, based on an underlying context. If the predictor is the Bayes optimal one, then computing the best matching based on the predicted weights is optimal. However, in practice, this perfect information scenario is not realistic. Given an imperfect predictor, a suboptimal decision rule may compensate for the induced error and thus outperform the standard optimal rule. In this paper, we propose multicalibration as a way to address this problem. This fairness notion requires a predictor to be unbiased on each element of a family of protected sets of contexts. Given a class of matching algorithms $\mathcal C$ and any predictor $γ$ of the edge-weights, we show how to construct a specific multicalibrated predictor $\hat γ$, with the following property. Picking the best matching based on the output of $\hat γ$ is competitive with the best decision rule in $\mathcal C$ applied onto the original predictor $γ$. We complement this result by providing sample complexity bounds.

A Tight VC-Dimension Analysis of Clustering Coresets with Applications

We consider coresets for $k$-clustering problems, where the goal is to assign points to centers minimizing powers of distances. A popular example is the $k$-median objective $\sum_{p}\min_{c\in C}dist(p,C)$. Given a point set $P$, a coreset $\Omega$ is a small weighted subset that approximates the cost of $P$ for all candidate solutions $C$ up to a $(1\pm\varepsilon )$ multiplicative factor. In this paper, we give a sharp VC-dimension based analysis for coreset construction. As a consequence, we obtain improved $k$-median coreset bounds for the following metrics: Coresets of size $\tilde{O}\left(k\varepsilon^{-2}\right)$ for shortest path metrics in planar graphs, improving over the bounds $\tilde{O}\left(k\varepsilon^{-6}\right)$ by [Cohen-Addad, Saulpic, Schwiegelshohn, STOC'21] and $\tilde{O}\left(k^2\varepsilon^{-4}\right)$ by [Braverman, Jiang, Krauthgamer, Wu, SODA'21]. Coresets of size $\tilde{O}\left(kd\ell\varepsilon^{-2}\log m\right)$ for clustering $d$-dimensional polygonal curves of length at most $m$ with curves of length at most $\ell$ with respect to Frechet metrics, improving over the bounds $\tilde{O}\left(k^3d\ell\varepsilon^{-3}\log m\right)$ by [Braverman, Cohen-Addad, Jiang, Krauthgamer, Schwiegelshohn, Toftrup, and Wu, FOCS'22] and $\tilde{O}\left(k^2d\ell\varepsilon^{-2}\log m \log |P|\right)$ by [Conradi, Kolbe, Psarros, Rohde, SoCG'24].

Online Learning with Sublinear Best-Action Queries

In online learning, a decision maker repeatedly selects one of a set of actions, with the goal of minimizing the overall loss incurred. Following the recent line of research on algorithms endowed with additional predictive features, we revisit this problem by allowing the decision maker to acquire additional information on the actions to be selected. In particular, we study the power of \emph{best-action queries}, which reveal beforehand the identity of the best action at a given time step. In practice, predictive features may be expensive, so we allow the decision maker to issue at most $k$ such queries. We establish tight bounds on the performance any algorithm can achieve when given access to $k$ best-action queries for different types of feedback models. In particular, we prove that in the full feedback model, $k$ queries are enough to achieve an optimal regret of $\Theta\left(\min\left\{\sqrt T, \frac Tk\right\}\right)$. This finding highlights the significant multiplicative advantage in the regret rate achievable with even a modest (sublinear) number $k \in \Omega(\sqrt{T})$ of queries. Additionally, we study the challenging setting in which the only available feedback is obtained during the time steps corresponding to the $k$ best-action queries. There, we provide a tight regret rate of $\Theta\left(\min\left\{\frac{T}{\sqrt k},\frac{T^2}{k^2}\right\}\right)$, which improves over the standard $\Theta\left(\frac{T}{\sqrt k}\right)$ regret rate for label efficient prediction for $k \in \Omega(T^{2/3})$.

Fully Dynamic Online Selection through Online Contention Resolution Schemes

We study fully dynamic online selection problems in an adversarial/stochastic setting that includes Bayesian online selection, prophet inequalities, posted price mechanisms, and stochastic probing problems subject to combinatorial constraints. In the classical ``incremental'' version of the problem, selected elements remain active until the end of the input sequence. On the other hand, in the fully dynamic version of the problem, elements stay active for a limited time interval, and then leave. This models, for example, the online matching of tasks to workers with task/worker-dependent working times, and sequential posted pricing of perishable goods. A successful approach to online selection problems in the adversarial setting is given by the notion of Online Contention Resolution Scheme (OCRS), that uses a priori information to formulate a linear relaxation of the underlying optimization problem, whose optimal fractional solution is rounded online for any adversarial order of the input sequence. Our main contribution is providing a general method for constructing an OCRS for fully dynamic online selection problems. Then, we show how to employ such OCRS to construct no-regret algorithms in a partial information model with semi-bandit feedback and adversarial inputs.

Poisoning Attacks with Generative Adversarial Nets

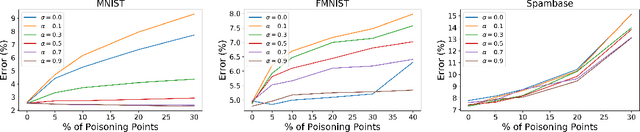
Machine learning algorithms are vulnerable to poisoning attacks: An adversary can inject malicious points in the training dataset to influence the learning process and degrade its performance. Optimal poisoning attacks have already been proposed to evaluate worst-case scenarios, modelling attacks as a bi-level optimisation problem. Solving these problems is computationally demanding and has limited applicability for some models such as deep networks. In this paper we introduce a novel generative model to craft systematic poisoning attacks against machine learning classifiers generating adversarial training examples, i.e. samples that look like genuine data points but that degrade the classifier's accuracy when used for training. We propose a Generative Adversarial Net with three components: generator, discriminator, and the target classifier. This approach allows us to model naturally the detectability constrains that can be expected in realistic attacks and to identify the regions of the underlying data distribution that can be more vulnerable to data poisoning. Our experimental evaluation shows the effectiveness of our attack to compromise machine learning classifiers, including deep networks.