Andrew Draganov
Phantom Transfer: Data-level Defences are Insufficient Against Data Poisoning
Feb 03, 2026Abstract:We present a data poisoning attack -- Phantom Transfer -- with the property that, even if you know precisely how the poison was placed into an otherwise benign dataset, you cannot filter it out. We achieve this by modifying subliminal learning to work in real-world contexts and demonstrate that the attack works across models, including GPT-4.1. Indeed, even fully paraphrasing every sample in the dataset using a different model does not stop the attack. We also discuss connections to steering vectors and show that one can plant password-triggered behaviours into models while still beating defences. This suggests that data-level defences are insufficient for stopping sophisticated data poisoning attacks. We suggest that future work should focus on model audits and white-box security methods.
Node Embeddings via Neighbor Embeddings
Mar 31, 2025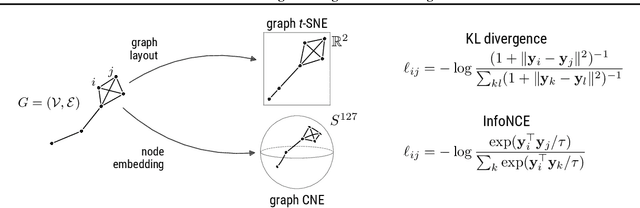
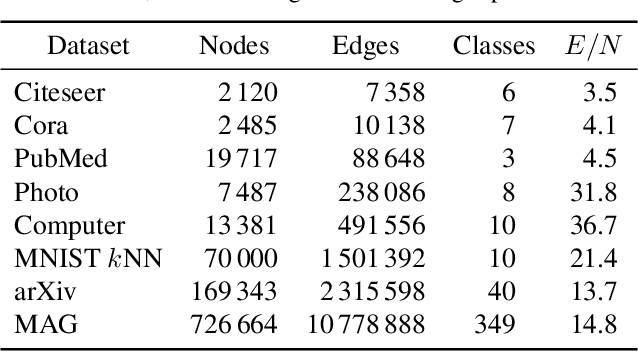
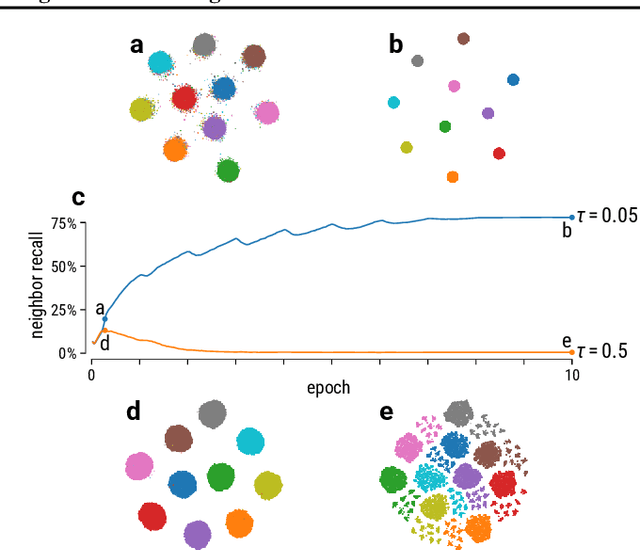
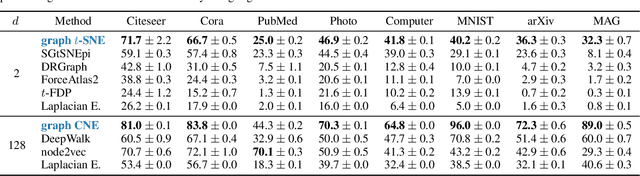
Abstract:Graph layouts and node embeddings are two distinct paradigms for non-parametric graph representation learning. In the former, nodes are embedded into 2D space for visualization purposes. In the latter, nodes are embedded into a high-dimensional vector space for downstream processing. State-of-the-art algorithms for these two paradigms, force-directed layouts and random-walk-based contrastive learning (such as DeepWalk and node2vec), have little in common. In this work, we show that both paradigms can be approached with a single coherent framework based on established neighbor embedding methods. Specifically, we introduce graph t-SNE, a neighbor embedding method for two-dimensional graph layouts, and graph CNE, a contrastive neighbor embedding method that produces high-dimensional node representations by optimizing the InfoNCE objective. We show that both graph t-SNE and graph CNE strongly outperform state-of-the-art algorithms in terms of local structure preservation, while being conceptually simpler.
I Want 'Em All (At Once) -- Ultrametric Cluster Hierarchies
Feb 19, 2025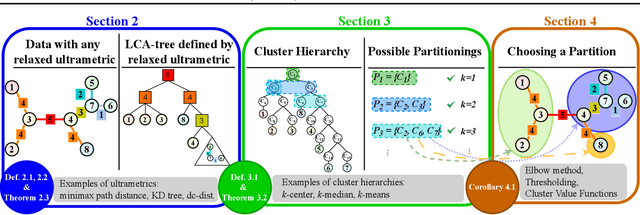

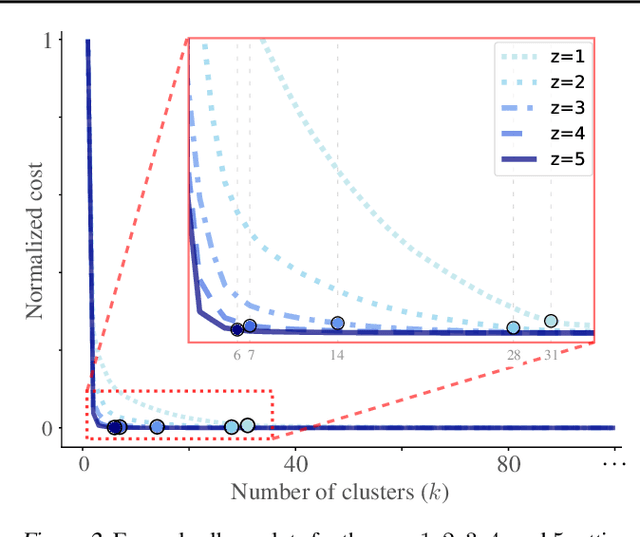
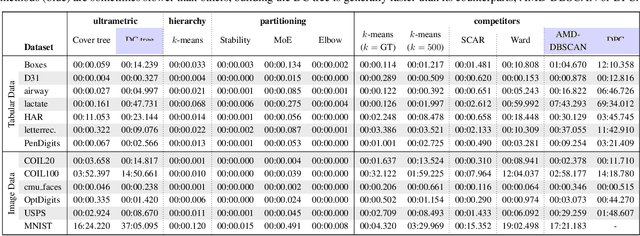
Abstract:Hierarchical clustering is a powerful tool for exploratory data analysis, organizing data into a tree of clusterings from which a partition can be chosen. This paper generalizes these ideas by proving that, for any reasonable hierarchy, one can optimally solve any center-based clustering objective over it (such as $k$-means). Moreover, these solutions can be found exceedingly quickly and are themselves necessarily hierarchical. Thus, given a cluster tree, we show that one can quickly access a plethora of new, equally meaningful hierarchies. Just as in standard hierarchical clustering, one can then choose any desired partition from these new hierarchies. We conclude by verifying the utility of our proposed techniques across datasets, hierarchies, and partitioning schemes.
On the Importance of Embedding Norms in Self-Supervised Learning
Feb 13, 2025Abstract:Self-supervised learning (SSL) allows training data representations without a supervised signal and has become an important paradigm in machine learning. Most SSL methods employ the cosine similarity between embedding vectors and hence effectively embed data on a hypersphere. While this seemingly implies that embedding norms cannot play any role in SSL, a few recent works have suggested that embedding norms have properties related to network convergence and confidence. In this paper, we resolve this apparent contradiction and systematically establish the embedding norm's role in SSL training. Using theoretical analysis, simulations, and experiments, we show that embedding norms (i) govern SSL convergence rates and (ii) encode network confidence, with smaller norms corresponding to unexpected samples. Additionally, we show that manipulating embedding norms can have large effects on convergence speed. Our findings demonstrate that SSL embedding norms are integral to understanding and optimizing network behavior.
A Tight VC-Dimension Analysis of Clustering Coresets with Applications
Jan 11, 2025


Abstract:We consider coresets for $k$-clustering problems, where the goal is to assign points to centers minimizing powers of distances. A popular example is the $k$-median objective $\sum_{p}\min_{c\in C}dist(p,C)$. Given a point set $P$, a coreset $\Omega$ is a small weighted subset that approximates the cost of $P$ for all candidate solutions $C$ up to a $(1\pm\varepsilon )$ multiplicative factor. In this paper, we give a sharp VC-dimension based analysis for coreset construction. As a consequence, we obtain improved $k$-median coreset bounds for the following metrics: Coresets of size $\tilde{O}\left(k\varepsilon^{-2}\right)$ for shortest path metrics in planar graphs, improving over the bounds $\tilde{O}\left(k\varepsilon^{-6}\right)$ by [Cohen-Addad, Saulpic, Schwiegelshohn, STOC'21] and $\tilde{O}\left(k^2\varepsilon^{-4}\right)$ by [Braverman, Jiang, Krauthgamer, Wu, SODA'21]. Coresets of size $\tilde{O}\left(kd\ell\varepsilon^{-2}\log m\right)$ for clustering $d$-dimensional polygonal curves of length at most $m$ with curves of length at most $\ell$ with respect to Frechet metrics, improving over the bounds $\tilde{O}\left(k^3d\ell\varepsilon^{-3}\log m\right)$ by [Braverman, Cohen-Addad, Jiang, Krauthgamer, Schwiegelshohn, Toftrup, and Wu, FOCS'22] and $\tilde{O}\left(k^2d\ell\varepsilon^{-2}\log m \log |P|\right)$ by [Conradi, Kolbe, Psarros, Rohde, SoCG'24].
The Hidden Pitfalls of the Cosine Similarity Loss
Jun 24, 2024Abstract:We show that the gradient of the cosine similarity between two points goes to zero in two under-explored settings: (1) if a point has large magnitude or (2) if the points are on opposite ends of the latent space. Counterintuitively, we prove that optimizing the cosine similarity between points forces them to grow in magnitude. Thus, (1) is unavoidable in practice. We then observe that these derivations are extremely general -- they hold across deep learning architectures and for many of the standard self-supervised learning (SSL) loss functions. This leads us to propose cut-initialization: a simple change to network initialization that helps all studied SSL methods converge faster.
Settling Time vs. Accuracy Tradeoffs for Clustering Big Data
Apr 02, 2024



Abstract:We study the theoretical and practical runtime limits of k-means and k-median clustering on large datasets. Since effectively all clustering methods are slower than the time it takes to read the dataset, the fastest approach is to quickly compress the data and perform the clustering on the compressed representation. Unfortunately, there is no universal best choice for compressing the number of points - while random sampling runs in sublinear time and coresets provide theoretical guarantees, the former does not enforce accuracy while the latter is too slow as the numbers of points and clusters grow. Indeed, it has been conjectured that any sensitivity-based coreset construction requires super-linear time in the dataset size. We examine this relationship by first showing that there does exist an algorithm that obtains coresets via sensitivity sampling in effectively linear time - within log-factors of the time it takes to read the data. Any approach that significantly improves on this must then resort to practical heuristics, leading us to consider the spectrum of sampling strategies across both real and artificial datasets in the static and streaming settings. Through this, we show the conditions in which coresets are necessary for preserving cluster validity as well as the settings in which faster, cruder sampling strategies are sufficient. As a result, we provide a comprehensive theoretical and practical blueprint for effective clustering regardless of data size. Our code is publicly available and has scripts to recreate the experiments.
Unexplainable Explanations: Towards Interpreting tSNE and UMAP Embeddings
Jun 20, 2023



Abstract:It has become standard to explain neural network latent spaces with attraction/repulsion dimensionality reduction (ARDR) methods like tSNE and UMAP. This relies on the premise that structure in the 2D representation is consistent with the structure in the model's latent space. However, this is an unproven assumption -- we are unaware of any convergence guarantees for ARDR algorithms. We work on closing this question by relating ARDR methods to classical dimensionality reduction techniques. Specifically, we show that one can fully recover a PCA embedding by applying attractions and repulsions onto a randomly initialized dataset. We also show that, with a small change, Locally Linear Embeddings (LLE) can reproduce ARDR embeddings. Finally, we formalize a series of conjectures that, if true, would allow one to attribute structure in the 2D embedding back to the input distribution.
ActUp: Analyzing and Consolidating tSNE and UMAP
May 12, 2023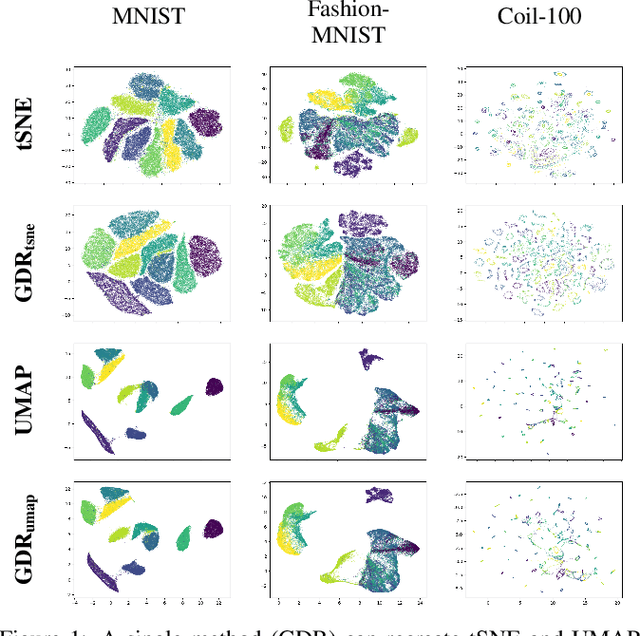

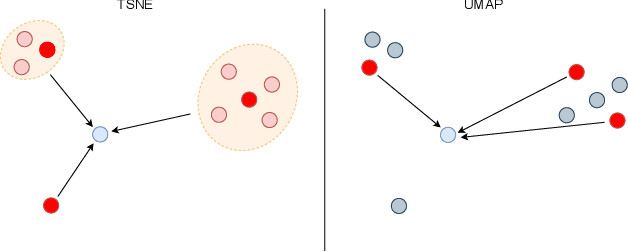
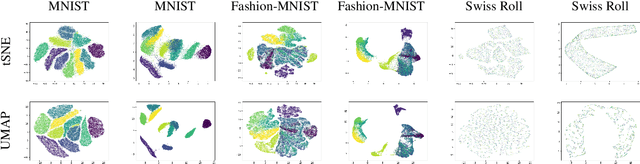
Abstract:tSNE and UMAP are popular dimensionality reduction algorithms due to their speed and interpretable low-dimensional embeddings. Despite their popularity, however, little work has been done to study their full span of differences. We theoretically and experimentally evaluate the space of parameters in both tSNE and UMAP and observe that a single one -- the normalization -- is responsible for switching between them. This, in turn, implies that a majority of the algorithmic differences can be toggled without affecting the embeddings. We discuss the implications this has on several theoretic claims behind UMAP, as well as how to reconcile them with existing tSNE interpretations. Based on our analysis, we provide a method (\ourmethod) that combines previously incompatible techniques from tSNE and UMAP and can replicate the results of either algorithm. This allows our method to incorporate further improvements, such as an acceleration that obtains either method's outputs faster than UMAP. We release improved versions of tSNE, UMAP, and \ourmethod that are fully plug-and-play with the traditional libraries at https://github.com/Andrew-Draganov/GiDR-DUN
GiDR-DUN; Gradient Dimensionality Reduction -- Differences and Unification
Jun 20, 2022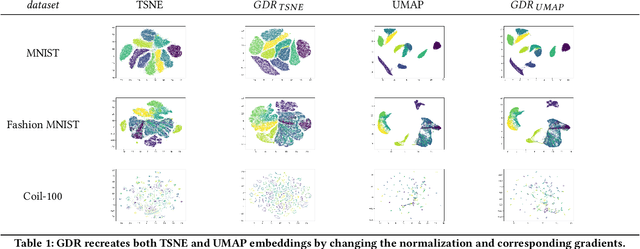
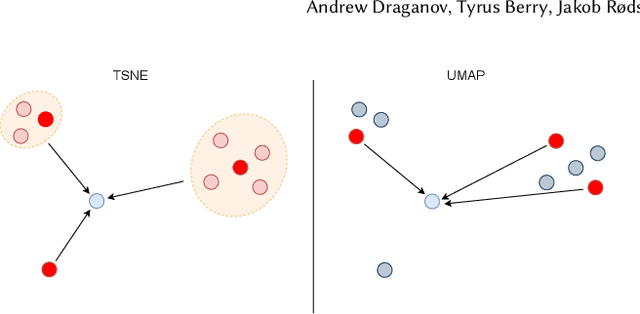
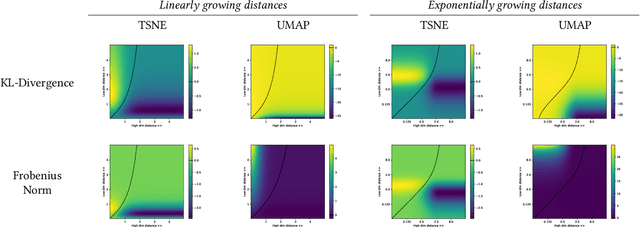

Abstract:TSNE and UMAP are two of the most popular dimensionality reduction algorithms due to their speed and interpretable low-dimensional embeddings. However, while attempts have been made to improve on TSNE's computational complexity, no existing method can obtain TSNE embeddings at the speed of UMAP. In this work, we show that this is indeed possible by combining the two approaches into a single method. We theoretically and experimentally evaluate the full space of parameters in the TSNE and UMAP algorithms and observe that a single parameter, the normalization, is responsible for switching between them. This, in turn, implies that a majority of the algorithmic differences can be toggled without affecting the embeddings. We discuss the implications this has on several theoretic claims underpinning the UMAP framework, as well as how to reconcile them with existing TSNE interpretations. Based on our analysis, we propose a new dimensionality reduction algorithm, GDR, that combines previously incompatible techniques from TSNE and UMAP and can replicate the results of either algorithm by changing the normalization. As a further advantage, GDR performs the optimization faster than available UMAP methods and thus an order of magnitude faster than available TSNE methods. Our implementation is plug-and-play with the traditional UMAP and TSNE libraries and can be found at github.com/Andrew-Draganov/GiDR-DUN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge