I Want 'Em All (At Once) -- Ultrametric Cluster Hierarchies

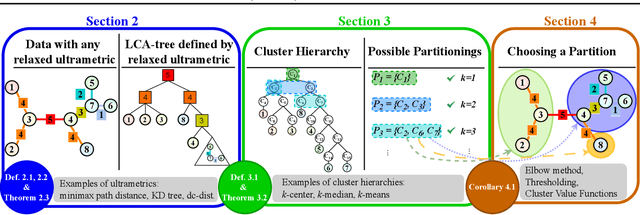
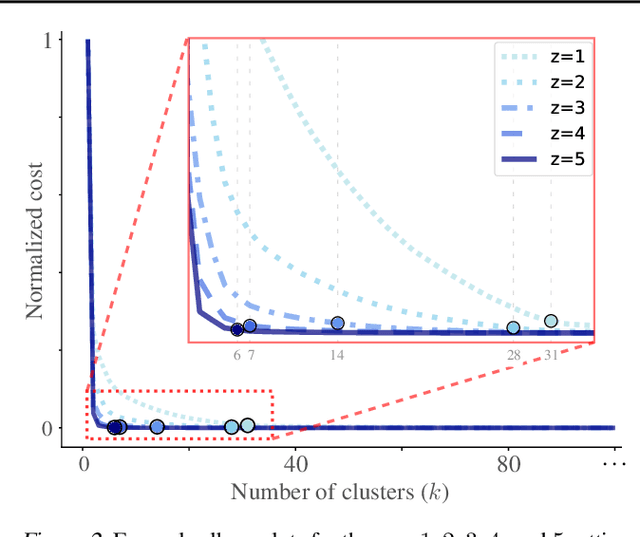
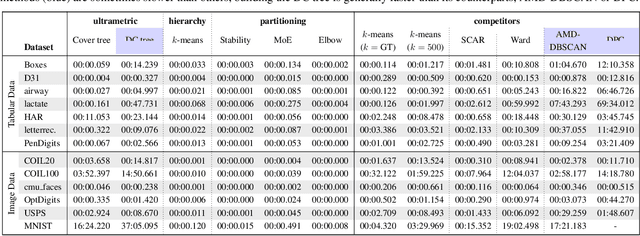
Hierarchical clustering is a powerful tool for exploratory data analysis, organizing data into a tree of clusterings from which a partition can be chosen. This paper generalizes these ideas by proving that, for any reasonable hierarchy, one can optimally solve any center-based clustering objective over it (such as $k$-means). Moreover, these solutions can be found exceedingly quickly and are themselves necessarily hierarchical. Thus, given a cluster tree, we show that one can quickly access a plethora of new, equally meaningful hierarchies. Just as in standard hierarchical clustering, one can then choose any desired partition from these new hierarchies. We conclude by verifying the utility of our proposed techniques across datasets, hierarchies, and partitioning schemes.

SHADE: Deep Density-based Clustering

Detecting arbitrarily shaped clusters in high-dimensional noisy data is challenging for current clustering methods. We introduce SHADE (Structure-preserving High-dimensional Analysis with Density-based Exploration), the first deep clustering algorithm that incorporates density-connectivity into its loss function. Similar to existing deep clustering algorithms, SHADE supports high-dimensional and large data sets with the expressive power of a deep autoencoder. In contrast to most existing deep clustering methods that rely on a centroid-based clustering objective, SHADE incorporates a novel loss function that captures density-connectivity. SHADE thereby learns a representation that enhances the separation of density-connected clusters. SHADE detects a stable clustering and noise points fully automatically without any user input. It outperforms existing methods in clustering quality, especially on data that contain non-Gaussian clusters, such as video data. Moreover, the embedded space of SHADE is suitable for visualization and interpretation of the clustering results as the individual shapes of the clusters are preserved.

Temporal Subspace Clustering for Molecular Dynamics Data

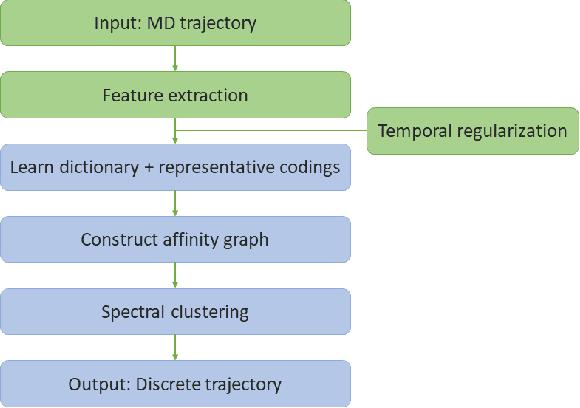
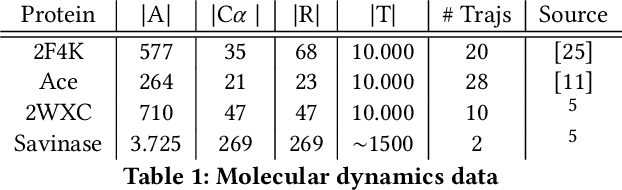
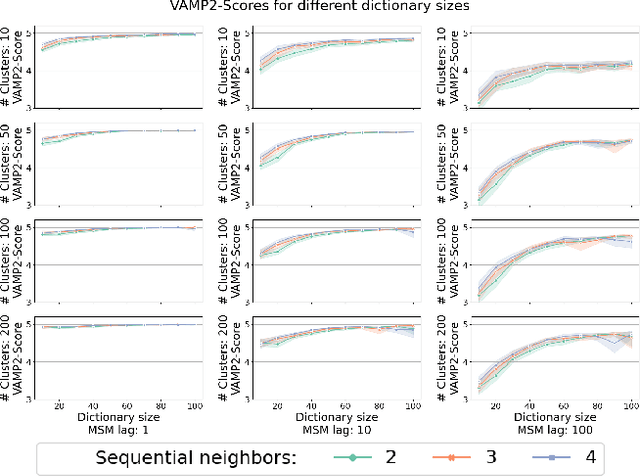
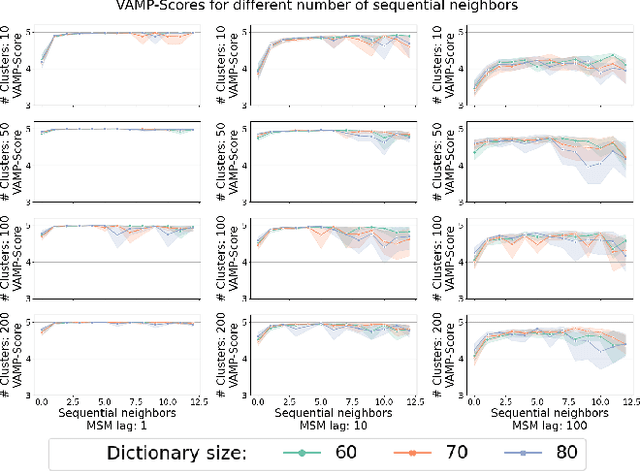
We introduce MOSCITO (MOlecular Dynamics Subspace Clustering with Temporal Observance), a subspace clustering for molecular dynamics data. MOSCITO groups those timesteps of a molecular dynamics trajectory together into clusters in which the molecule has similar conformations. In contrast to state-of-the-art methods, MOSCITO takes advantage of sequential relationships found in time series data. Unlike existing work, MOSCITO does not need a two-step procedure with tedious post-processing, but directly models essential properties of the data. Interpreting clusters as Markov states allows us to evaluate the clustering performance based on the resulting Markov state models. In experiments on 60 trajectories and 4 different proteins, we show that the performance of MOSCITO achieves state-of-the-art performance in a novel single-step method. Moreover, by modeling temporal aspects, MOSCITO obtains better segmentation of trajectories, especially for small numbers of clusters.