Bootstrap Deep Spectral Clustering with Optimal Transport

Spectral clustering is a leading clustering method. Two of its major shortcomings are the disjoint optimization process and the limited representation capacity. To address these issues, we propose a deep spectral clustering model (named BootSC), which jointly learns all stages of spectral clustering -- affinity matrix construction, spectral embedding, and $k$-means clustering -- using a single network in an end-to-end manner. BootSC leverages effective and efficient optimal-transport-derived supervision to bootstrap the affinity matrix and the cluster assignment matrix. Moreover, a semantically-consistent orthogonal re-parameterization technique is introduced to orthogonalize spectral embeddings, significantly enhancing the discrimination capability. Experimental results indicate that BootSC achieves state-of-the-art clustering performance. For example, it accomplishes a notable 16\% NMI improvement over the runner-up method on the challenging ImageNet-Dogs dataset. Our code is available at https://github.com/spdj2271/BootSC.

An Introductory Survey to Autoencoder-based Deep Clustering -- Sandboxes for Combining Clustering with Deep Learning

Autoencoders offer a general way of learning low-dimensional, non-linear representations from data without labels. This is achieved without making any particular assumptions about the data type or other domain knowledge. The generality and domain agnosticism in combination with their simplicity make autoencoders a perfect sandbox for researching and developing novel (deep) clustering algorithms. Clustering methods group data based on similarity, a task that benefits from the lower-dimensional representation learned by an autoencoder, mitigating the curse of dimensionality. Specifically, the combination of deep learning with clustering, called Deep Clustering, enables to learn a representation tailored to specific clustering tasks, leading to high-quality results. This survey provides an introduction to fundamental autoencoder-based deep clustering algorithms that serve as building blocks for many modern approaches.

SHADE: Deep Density-based Clustering

Detecting arbitrarily shaped clusters in high-dimensional noisy data is challenging for current clustering methods. We introduce SHADE (Structure-preserving High-dimensional Analysis with Density-based Exploration), the first deep clustering algorithm that incorporates density-connectivity into its loss function. Similar to existing deep clustering algorithms, SHADE supports high-dimensional and large data sets with the expressive power of a deep autoencoder. In contrast to most existing deep clustering methods that rely on a centroid-based clustering objective, SHADE incorporates a novel loss function that captures density-connectivity. SHADE thereby learns a representation that enhances the separation of density-connected clusters. SHADE detects a stable clustering and noise points fully automatically without any user input. It outperforms existing methods in clustering quality, especially on data that contain non-Gaussian clusters, such as video data. Moreover, the embedded space of SHADE is suitable for visualization and interpretation of the clustering results as the individual shapes of the clusters are preserved.

Automatic Parameter Selection for Non-Redundant Clustering

High-dimensional datasets often contain multiple meaningful clusterings in different subspaces. For example, objects can be clustered either by color, weight, or size, revealing different interpretations of the given dataset. A variety of approaches are able to identify such non-redundant clusterings. However, most of these methods require the user to specify the expected number of subspaces and clusters for each subspace. Stating these values is a non-trivial problem and usually requires detailed knowledge of the input dataset. In this paper, we propose a framework that utilizes the Minimum Description Length Principle (MDL) to detect the number of subspaces and clusters per subspace automatically. We describe an efficient procedure that greedily searches the parameter space by splitting and merging subspaces and clusters within subspaces. Additionally, an encoding strategy is introduced that allows us to detect outliers in each subspace. Extensive experiments show that our approach is highly competitive to state-of-the-art methods.

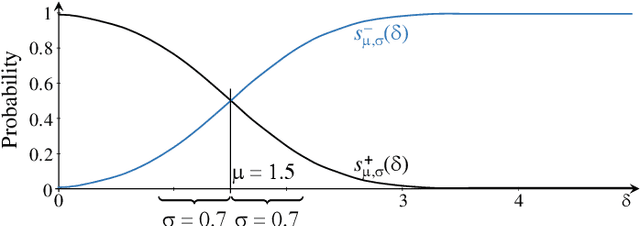
Extension of the Dip-test Repertoire -- Efficient and Differentiable p-value Calculation for Clustering

Over the last decade, the Dip-test of unimodality has gained increasing interest in the data mining community as it is a parameter-free statistical test that reliably rates the modality in one-dimensional samples. It returns a so called Dip-value and a corresponding probability for the sample's unimodality (Dip-p-value). These two values share a sigmoidal relationship. However, the specific transformation is dependent on the sample size. Many Dip-based clustering algorithms use bootstrapped look-up tables translating Dip- to Dip-p-values for a certain limited amount of sample sizes. We propose a specifically designed sigmoid function as a substitute for these state-of-the-art look-up tables. This accelerates computation and provides an approximation of the Dip- to Dip-p-value transformation for every single sample size. Further, it is differentiable and can therefore easily be integrated in learning schemes using gradient descent. We showcase this by exploiting our function in a novel subspace clustering algorithm called Dip'n'Sub. We highlight in extensive experiments the various benefits of our proposal.

Adversarial Anomaly Detection using Gaussian Priors and Nonlinear Anomaly Scores

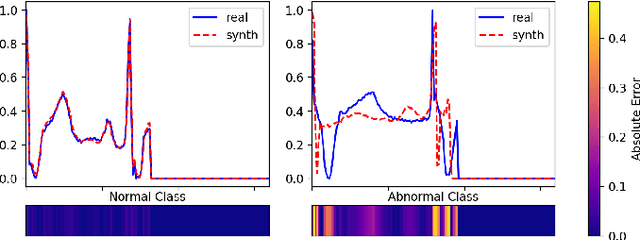
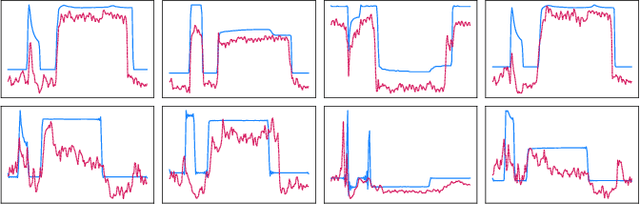
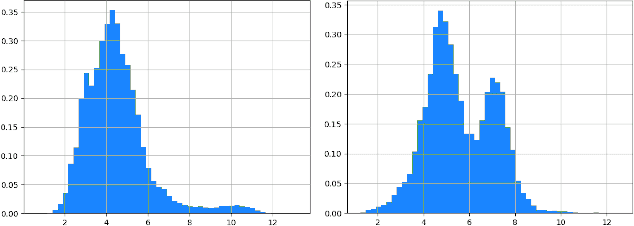
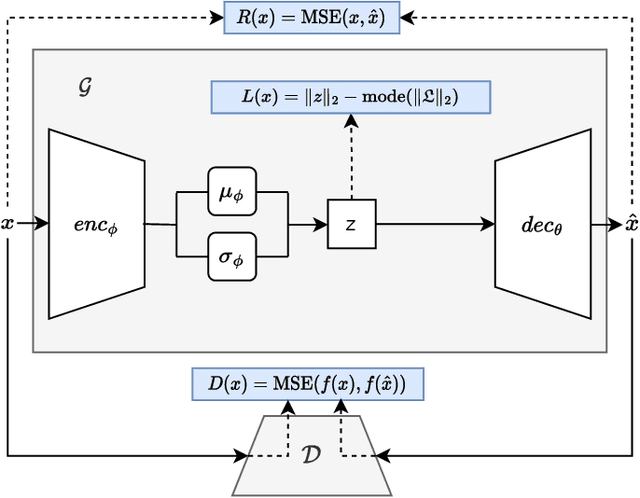
Anomaly detection in imbalanced datasets is a frequent and crucial problem, especially in the medical domain where retrieving and labeling irregularities is often expensive. By combining the generative stability of a $\beta$-variational autoencoder (VAE) with the discriminative strengths of generative adversarial networks (GANs), we propose a novel model, $\beta$-VAEGAN. We investigate methods for composing anomaly scores based on the discriminative and reconstructive capabilities of our model. Existing work focuses on linear combinations of these components to determine if data is anomalous. We advance existing work by training a kernelized support vector machine (SVM) on the respective error components to also consider nonlinear relationships. This improves anomaly detection performance, while allowing faster optimization. Lastly, we use the deviations from the Gaussian prior of $\beta$-VAEGAN to form a novel anomaly score component. In comparison to state-of-the-art work, we improve the $F_1$ score during anomaly detection from 0.85 to 0.92 on the widely used MITBIH Arrhythmia Database.

An Interpretable Neuron Embedding for Static Knowledge Distillation

Although deep neural networks have shown well-performance in various tasks, the poor interpretability of the models is always criticized. In the paper, we propose a new interpretable neural network method, by embedding neurons into the semantic space to extract their intrinsic global semantics. In contrast to previous methods that probe latent knowledge inside the model, the proposed semantic vector externalizes the latent knowledge to static knowledge, which is easy to exploit. Specifically, we assume that neurons with similar activation are of similar semantic information. Afterwards, semantic vectors are optimized by continuously aligning activation similarity and semantic vector similarity during the training of the neural network. The visualization of semantic vectors allows for a qualitative explanation of the neural network. Moreover, we assess the static knowledge quantitatively by knowledge distillation tasks. Empirical experiments of visualization show that semantic vectors describe neuron activation semantics well. Without the sample-by-sample guidance from the teacher model, static knowledge distillation exhibit comparable or even superior performance with existing relation-based knowledge distillation methods.

Deep Clustering With Consensus Representations

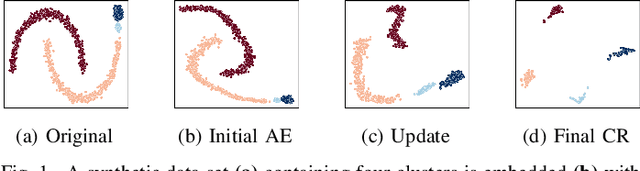
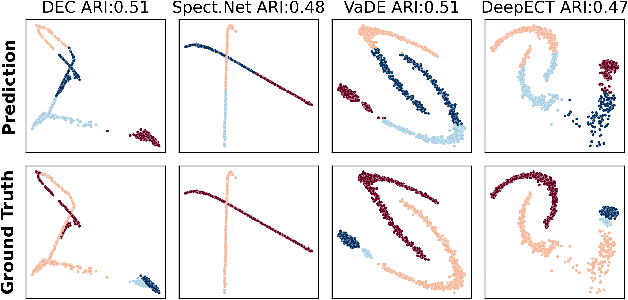
The field of deep clustering combines deep learning and clustering to learn representations that improve both the learned representation and the performance of the considered clustering method. Most existing deep clustering methods are designed for a single clustering method, e.g., k-means, spectral clustering, or Gaussian mixture models, but it is well known that no clustering algorithm works best in all circumstances. Consensus clustering tries to alleviate the individual weaknesses of clustering algorithms by building a consensus between members of a clustering ensemble. Currently, there is no deep clustering method that can include multiple heterogeneous clustering algorithms in an ensemble to update representations and clusterings together. To close this gap, we introduce the idea of a consensus representation that maximizes the agreement between ensemble members. Further, we propose DECCS (Deep Embedded Clustering with Consensus representationS), a deep consensus clustering method that learns a consensus representation by enhancing the embedded space to such a degree that all ensemble members agree on a common clustering result. Our contributions are the following: (1) We introduce the idea of learning consensus representations for heterogeneous clusterings, a novel notion to approach consensus clustering. (2) We propose DECCS, the first deep clustering method that jointly improves the representation and clustering results of multiple heterogeneous clustering algorithms. (3) We show in experiments that learning a consensus representation with DECCS is outperforming several relevant baselines from deep clustering and consensus clustering. Our code can be found at https://gitlab.cs.univie.ac.at/lukas/deccs

Massively Parallel Graph Drawing and Representation Learning

To fully exploit the performance potential of modern multi-core processors, machine learning and data mining algorithms for big data must be parallelized in multiple ways. Today's CPUs consist of multiple cores, each following an independent thread of control, and each equipped with multiple arithmetic units which can perform the same operation on a vector of multiple data objects. Graph embedding, i.e. converting the vertices of a graph into numerical vectors is a data mining task of high importance and is useful for graph drawing (low-dimensional vectors) and graph representation learning (high-dimensional vectors). In this paper, we propose MulticoreGEMPE (Graph Embedding by Minimizing the Predictive Entropy), an information-theoretic method which can generate low and high-dimensional vectors. MulticoreGEMPE applies MIMD (Multiple Instructions Multiple Data, using OpenMP) and SIMD (Single Instructions Multiple Data, using AVX-512) parallelism. We propose general ideas applicable in other graph-based algorithms like \emph{vectorized hashing} and \emph{vectorized reduction}. Our experimental evaluation demonstrates the superiority of our approach.

Space-filling Curves for High-performance Data Mining

Space-filling curves like the Hilbert-curve, Peano-curve and Z-order map natural or real numbers from a two or higher dimensional space to a one dimensional space preserving locality. They have numerous applications like search structures, computer graphics, numerical simulation, cryptographics and can be used to make various algorithms cache-oblivious. In this paper, we describe some details of the Hilbert-curve. We define the Hilbert-curve in terms of a finite automaton of Mealy-type which determines from the two-dimensional coordinate space the Hilbert order value and vice versa in a logarithmic number of steps. And we define a context-free grammar to generate the whole curve in a time which is linear in the number of generated coordinate/order value pairs, i.e. a constant time per coordinate pair or order value. We also review two different strategies which enable the generation of curves without the usual restriction to square-like grids where the side-length is a power of two. Finally, we elaborate on a few applications, namely matrix multiplication, Cholesky decomposition, the Floyd-Warshall algorithm, k-Means clustering, and the similarity join.