Dominik Mautz
Automatic Parameter Selection for Non-Redundant Clustering
Dec 19, 2023



Abstract:High-dimensional datasets often contain multiple meaningful clusterings in different subspaces. For example, objects can be clustered either by color, weight, or size, revealing different interpretations of the given dataset. A variety of approaches are able to identify such non-redundant clusterings. However, most of these methods require the user to specify the expected number of subspaces and clusters for each subspace. Stating these values is a non-trivial problem and usually requires detailed knowledge of the input dataset. In this paper, we propose a framework that utilizes the Minimum Description Length Principle (MDL) to detect the number of subspaces and clusters per subspace automatically. We describe an efficient procedure that greedily searches the parameter space by splitting and merging subspaces and clusters within subspaces. Additionally, an encoding strategy is introduced that allows us to detect outliers in each subspace. Extensive experiments show that our approach is highly competitive to state-of-the-art methods.
Incorporating User's Preference into Attributed Graph Clustering
Mar 24, 2020
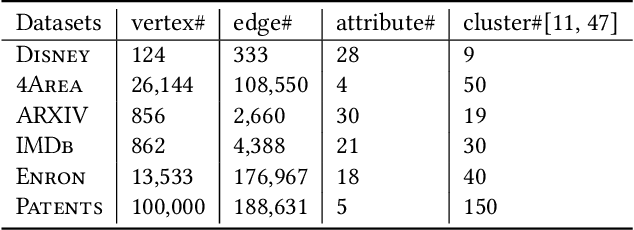
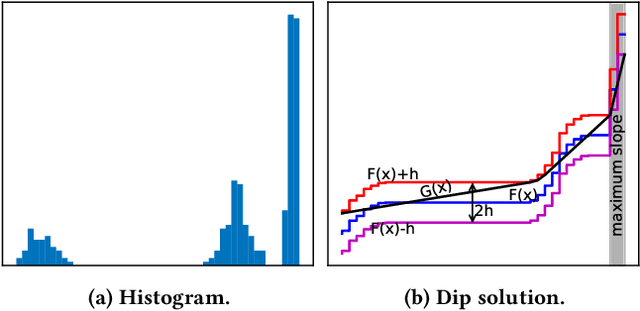
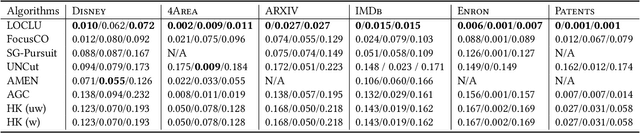
Abstract:Graph clustering has been studied extensively on both plain graphs and attributed graphs. However, all these methods need to partition the whole graph to find cluster structures. Sometimes, based on domain knowledge, people may have information about a specific target region in the graph and only want to find a single cluster concentrated on this local region. Such a task is called local clustering. In contrast to global clustering, local clustering aims to find only one cluster that is concentrating on the given seed vertex (and also on the designated attributes for attributed graphs). Currently, very few methods can deal with this kind of task. To this end, we propose two quality measures for a local cluster: Graph Unimodality (GU) and Attribute Unimodality (AU). The former measures the homogeneity of the graph structure while the latter measures the homogeneity of the subspace that is composed of the designated attributes. We call their linear combination as Compactness. Further, we propose LOCLU to optimize the Compactness score. The local cluster detected by LOCLU concentrates on the region of interest, provides efficient information flow in the graph and exhibits a unimodal data distribution in the subspace of the designated attributes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge