Dual-Phase Cross-Modal Contrastive Learning for CMR-Guided ECG Representations for Cardiovascular Disease Assessment

Cardiac magnetic resonance imaging (CMR) offers detailed evaluation of cardiac structure and function, but its limited accessibility restricts use to selected patient populations. In contrast, the electrocardiogram (ECG) is ubiquitous and inexpensive, and provides rich information on cardiac electrical activity and rhythm, yet offers limited insight into underlying cardiac structure and mechanical function. To address this, we introduce a contrastive learning framework that improves the extraction of clinically relevant cardiac phenotypes from ECG by learning from paired ECG-CMR data. Our approach aligns ECG representations with 3D CMR volumes at end-diastole (ED) and end-systole (ES), with a dual-phase contrastive loss to anchor each ECG jointly with both cardiac phases in a shared latent space. Unlike prior methods limited to 2D CMR representations with or without a temporal component, our framework models 3D anatomy at both ED and ES phases as distinct latent representations, enabling flexible disentanglement of structural and functional cardiac properties. Using over 34,000 ECG-CMR pairs from the UK Biobank, we demonstrate improved extraction of image-derived phenotypes from ECG, particularly for functional parameters ($\uparrow$ 9.2\%), while improvements in clinical outcome prediction remained modest ($\uparrow$ 0.7\%). This strategy could enable scalable and cost-effective extraction of image-derived traits from ECG. The code for this research is publicly available.

Synthesis of Late Gadolinium Enhancement Images via Implicit Neural Representations for Cardiac Scar Segmentation

Late gadolinium enhancement (LGE) imaging is the clinical standard for myocardial scar assessment, but limited annotated datasets hinder the development of automated segmentation methods. We propose a novel framework that synthesises both LGE images and their corresponding segmentation masks using implicit neural representations (INRs) combined with denoising diffusion models. Our approach first trains INRs to capture continuous spatial representations of LGE data and associated myocardium and fibrosis masks. These INRs are then compressed into compact latent embeddings, preserving essential anatomical information. A diffusion model operates on this latent space to generate new representations, which are decoded into synthetic LGE images with anatomically consistent segmentation masks. Experiments on 133 cardiac MRI scans suggest that augmenting training data with 200 synthetic volumes contributes to improved fibrosis segmentation performance, with the Dice score showing an increase from 0.509 to 0.524. Our approach provides an annotation-free method to help mitigate data scarcity.The code for this research is publicly available.

Equivariant Eikonal Neural Networks: Grid-Free, Scalable Travel-Time Prediction on Homogeneous Spaces

We introduce Equivariant Neural Eikonal Solvers, a novel framework that integrates Equivariant Neural Fields (ENFs) with Neural Eikonal Solvers. Our approach employs a single neural field where a unified shared backbone is conditioned on signal-specific latent variables - represented as point clouds in a Lie group - to model diverse Eikonal solutions. The ENF integration ensures equivariant mapping from these latent representations to the solution field, delivering three key benefits: enhanced representation efficiency through weight-sharing, robust geometric grounding, and solution steerability. This steerability allows transformations applied to the latent point cloud to induce predictable, geometrically meaningful modifications in the resulting Eikonal solution. By coupling these steerable representations with Physics-Informed Neural Networks (PINNs), our framework accurately models Eikonal travel-time solutions while generalizing to arbitrary Riemannian manifolds with regular group actions. This includes homogeneous spaces such as Euclidean, position-orientation, spherical, and hyperbolic manifolds. We validate our approach through applications in seismic travel-time modeling of 2D and 3D benchmark datasets. Experimental results demonstrate superior performance, scalability, adaptability, and user controllability compared to existing Neural Operator-based Eikonal solver methods.

Orientation Scores should be a Piece of Cake

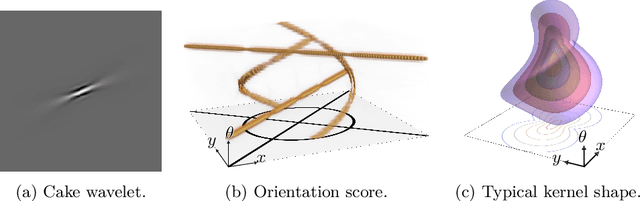
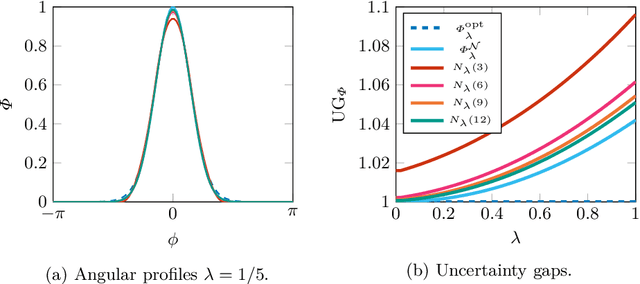
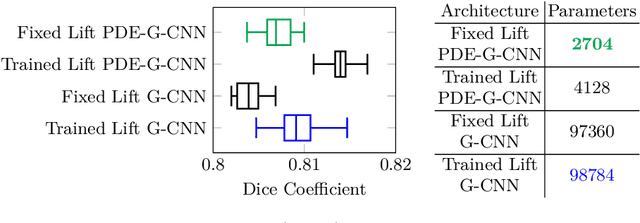
We axiomatically derive a family of wavelets for an orientation score, lifting from position space $\mathbb{R}^2$ to position and orientation space $\mathbb{R}^2\times S^1$, with fast reconstruction property, that minimise position-orientation uncertainty. We subsequently show that these minimum uncertainty states are well-approximated by cake wavelets: for standard parameters, the uncertainty gap of cake wavelets is less than 1.1, and in the limit, we prove the uncertainty gap tends to the minimum of 1. Next, we complete a previous theoretical argument that one does not have to train the lifting layer in (PDE-)G-CNNs, but can instead use cake wavelets. Finally, we show experimentally that in this way we can reduce the network complexity and improve the interpretability of (PDE-)G-CNNs, with only a slight impact on the model's performance.

Towards Variational Flow Matching on General Geometries

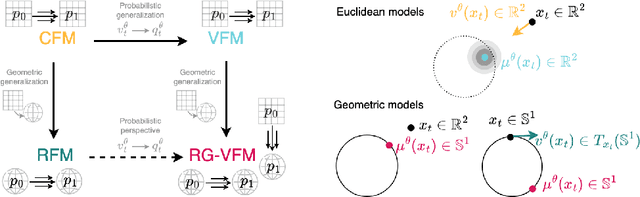
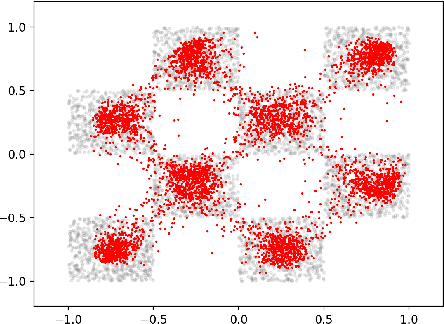
We introduce Riemannian Gaussian Variational Flow Matching (RG-VFM), an extension of Variational Flow Matching (VFM) that leverages Riemannian Gaussian distributions for generative modeling on structured manifolds. We derive a variational objective for probability flows on manifolds with closed-form geodesics, making RG-VFM comparable - though fundamentally different to Riemannian Flow Matching (RFM) in this geometric setting. Experiments on a checkerboard dataset wrapped on the sphere demonstrate that RG-VFM captures geometric structure more effectively than Euclidean VFM and baseline methods, establishing it as a robust framework for manifold-aware generative modeling.

Learning Symmetries via Weight-Sharing with Doubly Stochastic Tensors

Group equivariance has emerged as a valuable inductive bias in deep learning, enhancing generalization, data efficiency, and robustness. Classically, group equivariant methods require the groups of interest to be known beforehand, which may not be realistic for real-world data. Additionally, baking in fixed group equivariance may impose overly restrictive constraints on model architecture. This highlights the need for methods that can dynamically discover and apply symmetries as soft constraints. For neural network architectures, equivariance is commonly achieved through group transformations of a canonical weight tensor, resulting in weight sharing over a given group $G$. In this work, we propose to learn such a weight-sharing scheme by defining a collection of learnable doubly stochastic matrices that act as soft permutation matrices on canonical weight tensors, which can take regular group representations as a special case. This yields learnable kernel transformations that are jointly optimized with downstream tasks. We show that when the dataset exhibits strong symmetries, the permutation matrices will converge to regular group representations and our weight-sharing networks effectively become regular group convolutions. Additionally, the flexibility of the method enables it to effectively pick up on partial symmetries.

The Hidden Pitfalls of the Cosine Similarity Loss

We show that the gradient of the cosine similarity between two points goes to zero in two under-explored settings: (1) if a point has large magnitude or (2) if the points are on opposite ends of the latent space. Counterintuitively, we prove that optimizing the cosine similarity between points forces them to grow in magnitude. Thus, (1) is unavoidable in practice. We then observe that these derivations are extremely general -- they hold across deep learning architectures and for many of the standard self-supervised learning (SSL) loss functions. This leads us to propose cut-initialization: a simple change to network initialization that helps all studied SSL methods converge faster.

Space-Time Continuous PDE Forecasting using Equivariant Neural Fields

Recently, Conditional Neural Fields (NeFs) have emerged as a powerful modelling paradigm for PDEs, by learning solutions as flows in the latent space of the Conditional NeF. Although benefiting from favourable properties of NeFs such as grid-agnosticity and space-time-continuous dynamics modelling, this approach limits the ability to impose known constraints of the PDE on the solutions -- e.g. symmetries or boundary conditions -- in favour of modelling flexibility. Instead, we propose a space-time continuous NeF-based solving framework that - by preserving geometric information in the latent space - respects known symmetries of the PDE. We show that modelling solutions as flows of pointclouds over the group of interest $G$ improves generalization and data-efficiency. We validated that our framework readily generalizes to unseen spatial and temporal locations, as well as geometric transformations of the initial conditions - where other NeF-based PDE forecasting methods fail - and improve over baselines in a number of challenging geometries.

E(n) Equivariant Message Passing Cellular Networks

This paper introduces E(n) Equivariant Message Passing Cellular Networks (EMPCNs), an extension of E(n) Equivariant Graph Neural Networks to CW-complexes. Our approach addresses two aspects of geometric message passing networks: 1) enhancing their expressiveness by incorporating arbitrary cells, and 2) achieving this in a computationally efficient way with a decoupled EMPCNs technique. We demonstrate that EMPCNs achieve close to state-of-the-art performance on multiple tasks without the need for steerability, including many-body predictions and motion capture. Moreover, ablation studies confirm that decoupled EMPCNs exhibit stronger generalization capabilities than their non-topologically informed counterparts. These findings show that EMPCNs can be used as a scalable and expressive framework for higher-order message passing in geometric and topological graphs

Latent Field Discovery In Interacting Dynamical Systems With Neural Fields

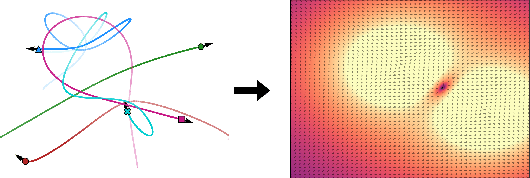
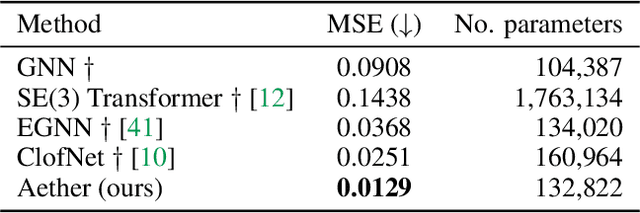
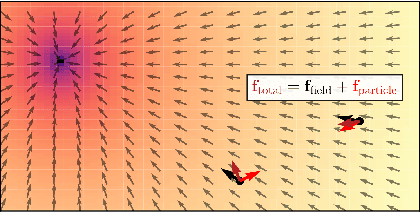
Systems of interacting objects often evolve under the influence of field effects that govern their dynamics, yet previous works have abstracted away from such effects, and assume that systems evolve in a vacuum. In this work, we focus on discovering these fields, and infer them from the observed dynamics alone, without directly observing them. We theorize the presence of latent force fields, and propose neural fields to learn them. Since the observed dynamics constitute the net effect of local object interactions and global field effects, recently popularized equivariant networks are inapplicable, as they fail to capture global information. To address this, we propose to disentangle local object interactions -- which are $\mathrm{SE}(n)$ equivariant and depend on relative states -- from external global field effects -- which depend on absolute states. We model interactions with equivariant graph networks, and combine them with neural fields in a novel graph network that integrates field forces. Our experiments show that we can accurately discover the underlying fields in charged particles settings, traffic scenes, and gravitational n-body problems, and effectively use them to learn the system and forecast future trajectories.