Learning Symmetries via Weight-Sharing with Doubly Stochastic Tensors

Group equivariance has emerged as a valuable inductive bias in deep learning, enhancing generalization, data efficiency, and robustness. Classically, group equivariant methods require the groups of interest to be known beforehand, which may not be realistic for real-world data. Additionally, baking in fixed group equivariance may impose overly restrictive constraints on model architecture. This highlights the need for methods that can dynamically discover and apply symmetries as soft constraints. For neural network architectures, equivariance is commonly achieved through group transformations of a canonical weight tensor, resulting in weight sharing over a given group $G$. In this work, we propose to learn such a weight-sharing scheme by defining a collection of learnable doubly stochastic matrices that act as soft permutation matrices on canonical weight tensors, which can take regular group representations as a special case. This yields learnable kernel transformations that are jointly optimized with downstream tasks. We show that when the dataset exhibits strong symmetries, the permutation matrices will converge to regular group representations and our weight-sharing networks effectively become regular group convolutions. Additionally, the flexibility of the method enables it to effectively pick up on partial symmetries.

Conformal time series decomposition with component-wise exchangeability

Conformal prediction offers a practical framework for distribution-free uncertainty quantification, providing finite-sample coverage guarantees under relatively mild assumptions on data exchangeability. However, these assumptions cease to hold for time series due to their temporally correlated nature. In this work, we present a novel use of conformal prediction for time series forecasting that incorporates time series decomposition. This approach allows us to model different temporal components individually. By applying specific conformal algorithms to each component and then merging the obtained prediction intervals, we customize our methods to account for the different exchangeability regimes underlying each component. Our decomposition-based approach is thoroughly discussed and empirically evaluated on synthetic and real-world data. We find that the method provides promising results on well-structured time series, but can be limited by factors such as the decomposition step for more complex data.

Learned Gridification for Efficient Point Cloud Processing

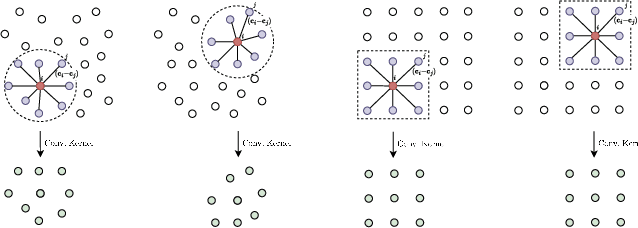
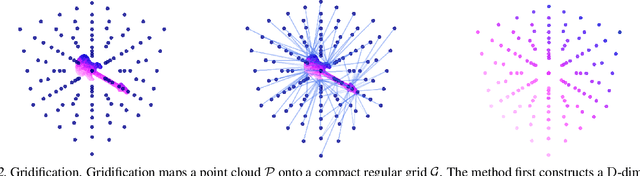
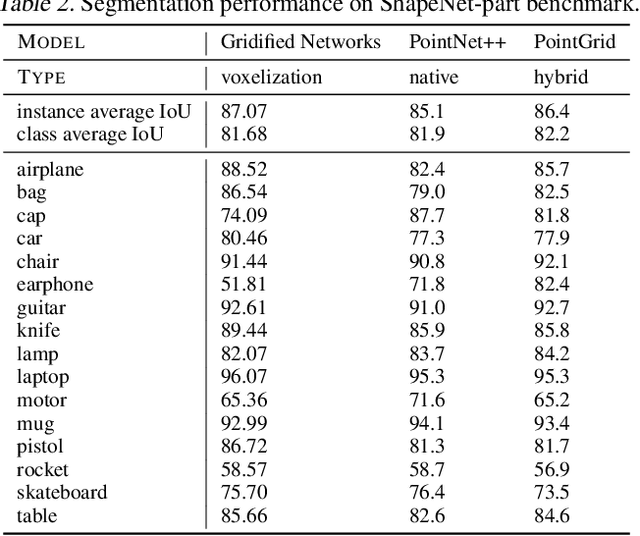
Neural operations that rely on neighborhood information are much more expensive when deployed on point clouds than on grid data due to the irregular distances between points in a point cloud. In a grid, on the other hand, we can compute the kernel only once and reuse it for all query positions. As a result, operations that rely on neighborhood information scale much worse for point clouds than for grid data, specially for large inputs and large neighborhoods. In this work, we address the scalability issue of point cloud methods by tackling its root cause: the irregularity of the data. We propose learnable gridification as the first step in a point cloud processing pipeline to transform the point cloud into a compact, regular grid. Thanks to gridification, subsequent layers can use operations defined on regular grids, e.g., Conv3D, which scale much better than native point cloud methods. We then extend gridification to point cloud to point cloud tasks, e.g., segmentation, by adding a learnable de-gridification step at the end of the point cloud processing pipeline to map the compact, regular grid back to its original point cloud form. Through theoretical and empirical analysis, we show that gridified networks scale better in terms of memory and time than networks directly applied on raw point cloud data, while being able to achieve competitive results. Our code is publicly available at https://github.com/computri/gridifier.